Übersicht über Maßeinheiten – Länge, Fläche, Volumen, Gewicht und Zeit
Alles über Maßeinheiten: Eine einfache Einführung in die eindeutige Messung von Größen wie Länge und Zeit. Entdecke die Vielfalt an Basiseinheiten, unterstützt von Vorsatzzeichen für verschiedene Größenordnungen. Bereit zum Umrechnen? Dies und vieles mehr findest du im folgenden Text.
Inhaltsverzeichnis zum Thema Maßeinheiten
Maßeinheiten im Überblick
Quelle sofatutor.com
Maßeinheiten für Größen
Um physikalische Größen wie Längen oder Zeit vergleichen zu können, werden diese in eindeutig festgelegten Maßeinheiten gemessen und angegeben. Eine Größenangabe besteht in Mathe stets aus der Maßzahl und der Maßeinheit. So schreiben wir beispielsweise für eine Zeit von 
Minuten:
Für jede Art von Größe gibt es eine Basiseinheit:
- Meter
für Längen - Gramm
für Masse oder Gewicht - Sekunde
für Zeit - Quadratmeter
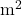für Flächen - Kubikmeter
für Volumen
Um auch besonders kleine oder große Werte darstellen zu können, werden bei den meisten Einheiten Vorsatzzeichen verwendet, die Vielfache oder Teile der Maßeinheit bilden.
Die gängigen Vorsatzzeichen für alle Maßeinheiten sind in der Tabelle der Reihenfolge nach zusammengefasst.
Die Zehnerpotenz gibt dabei an, um welchen Umrechnungsfaktor von der Basiseinheit abgewichen wird. Zum Beispiel entspricht ein Kilometer 
Metern:
Ein Millimeter ist dagegen der tausendste Teil eines Meters:
| Zeichen | Name | Zehnerpotenz |
|---|---|---|
 |
Pico |  |
 |
Nano |  |
 |
Mikro |  |
|
Milli |  |
 |
Zenti |  |
 |
Dezi |  |
 |
Deka |  |
 |
Hekto |  |
 |
Kilo |  |
 |
Mega |  |
 |
Giga |  |
 |
Tera |  |
Maßeinheiten umrechnen
Wenn wir mit Maßeinheiten rechnen, ist es ratsam, zunächst alle Größen in einem Term in die gleiche Maßeinheit umzuwandeln. Dazu nutzen wir die Zehnerpotenzen aus der obigen Tabelle.
Wie das Umrechnen von Maßeinheiten funktioniert, lässt sich an einem Beispiel einfach erklären. Wir wollen dazu die Summe aus verschiedenen Gewichten bilden:
Zunächst wandeln wir alle Größen in die Einheit Gramm um:
In unserem Lerntext erfährst du mehr über die Umrechnung von Gewichten.
Maßeinheiten – Übersicht
Im Folgenden betrachten wir die verschiedenen Größeneinheiten für Zeit, Gewicht, Länge, Fläche und Volumen.
Gewicht
Um das Gewicht oder die Masse von Objekten zu messen, wird die Basiseinheit Gramm mit den entsprechenden Vorsatzzeichen verwendet. Dabei entsprechen zum Beispiel 
Gramm einem Kilogramm: 
.
Für eine Masse von Kilogramm und darüber ist die Einheit Tonne üblich:
Es gibt beim Gewicht einige alte Maßeinheiten für bestimmte Mengen:
- Ein Pfund entspricht
Gramm. - Ein Zentner entspricht
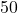Kilogramm.
Gewichtseinheiten Rechner
Länge, Fläche und Volumen
Die Maßeinheiten für Entfernungen, Flächen und Rauminhalte basieren alle auf der Basiseinheit Meter () mit den entsprechenden Vorsatzzeichen.
Längenmaße
Mit Längenmaßen wie Meter (), Zentimeter (
) und Kilometer (
) werden Entfernungen angegeben.
Flächenmaße
Zur Messung von Flächen werden sogenannte Einheitsquadrate genutzt. Daher werden Flächenmaße zum Beispiel in den Einheiten Quadratmeter (), Quadratzentimeter (
) oder Quadratkilometer (
) angegeben.
Da der Schritt zwischen Quadratmeter und Quadratkilometer sehr groß ist (
), gibt es dazwischen die zum Beispiel in der Landwirtschaft gebräuchlichen Maßeinheiten Ar (
) und Hektar (
). Dabei gilt:
Volumen- oder Hohlmaße
Der Rauminhalt von Körpern kann durch Einheitswürfel gemessen werden. Aufgrund der drei Kantenlängen ergeben sich als Einheiten zum Beispiel Kubikmeter (), Kubikzentimeter (
) oder Kubikkilometer (
).
Alternativ werden auch sogenannte Hohlmaße mit der Basiseinheit Liter 
genutzt. Dabei gilt:
Die folgende Tabelle fasst die Maßeinheiten für Flüssigkeiten in Liter zusammen:
| Name | Einheit | Entsprechung |
|---|---|---|
| Milliliter |  |
 |
| Zentiliter |  |
 |
| Liter | |
 |
| Hektoliter |  |
 |
Die Umrechnung für Längen-, Flächen- und Volumeneinheiten wird in der Abbildung zusammengefasst:
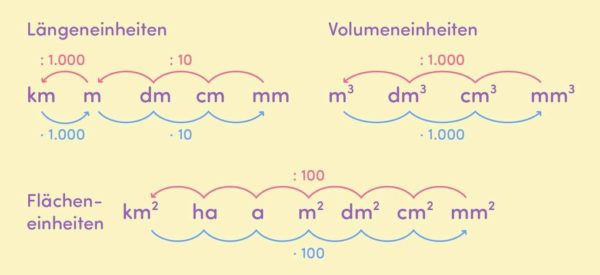
Zeit
Die Zeit wird in Sekunden (), Minuten (
), Stunden (), Tagen () und Jahren () gemessen. Hier unterscheidet sich die Einteilung von den üblichen Zehnerpotenzen. Es gilt:
- Eine Minute hat
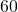Sekunden. - Eine Stunde hat 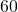Minuten.
- Ein Tag hat
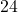Stunden. - Ein Jahr hat
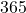Tage.
Wir fassen die Faktoren in einer Umrechnungstabelle für die Maßeinheiten der Zeit zusammen:
| Umrechnung | in |
in |
in |
in |
in |
|---|---|---|---|---|---|
| von |
 |
 |
 |
 |
 |
| von |
|
|
|
 |
 |
| von |
 |
|
|
 |
 |
| von |
 |
 |
|
|
 |
| von |
 |
 |
 |
|
|
Hinweis: Bei der Messung von Zeiten unter einer Sekunde werden die gängigen Vorsatzzeichen verwendet, beispielsweise 
für Millisekunden.
Zeiteinheiten Rechner
Häufig gestellte Fragen zum Thema Maßeinheiten
Maßeinheiten sind eindeutig festgelegte Einheiten zur Messung physikalischer Größen.
Die einheitlichen Maßeinheiten wurden eingeführt, um Messungen vergleichbar zu machen.
Zwischen kleineren und größeren Maßeinheiten wird durch Multiplikation mit dem passenden Umrechnungsfaktor umgerechnet.
Es gibt Maßeinheiten für verschiedene Größen zum Beispiel:
- Sekunden für Zeit
- Meter für Länge
- Gramm für Gewicht
Die Größe einer Maßeinheit ergibt sich aus der Vorsilbe. Für eine Einheit der gebräuchlichsten Maße gilt:
Milli– < Zenti– < Dezi– < Deka– < Hekto– < Kilo–
Massen oder Gewichte werden in Gramm () gemessen.
Die kleinste gebräuchliche Längeneinheit ist der Millimeter (
). Noch kleinere Längen können in Mikro-, Nano-, Piko-, Femto– oder Attometer angegeben werden.
Längen werden üblicherweise in Metern gemessen. Es gibt auch andere Längeneinheiten, wie Zoll, Fuß oder Meile, die beispielsweise im englischsprachigen Raum verbreitet sind.
Beispiele für alte Maßeinheiten sind:
- das Pfund ( Gramm)
- der Hektar (
Quadratmeter)
Die Maßeinheiten für verschiedene Größen haben verschiedene Bezeichnungen. Für einen Großteil der Maßeinheiten gelten dieselben Vorsilben, durch die die Einheiten vergrößert oder verkleinert werden.
Das Umrechnen von Maßeinheiten kann anhand der Umrechnungsfaktoren erklärt werden.