Trigonometrie – Erklärung, Definitionen und Formeln
Lerne, wie Trigonometrie Teil der Geometrie ist und sich mit Winkelbeziehungen in rechtwinkligen Dreiecken befasst. Lerne die wichtigen trigonometrischen Funktionen Sinus, Cosinus und Tangens sowie den Satz des Pythagoras kennen.
Inhaltsverzeichnis zum Thema Trigonometrie
Trigonometrie – Einführung und Grundlagen
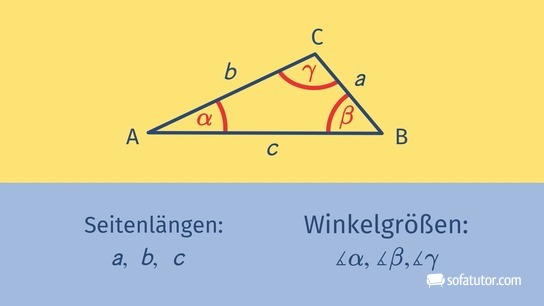
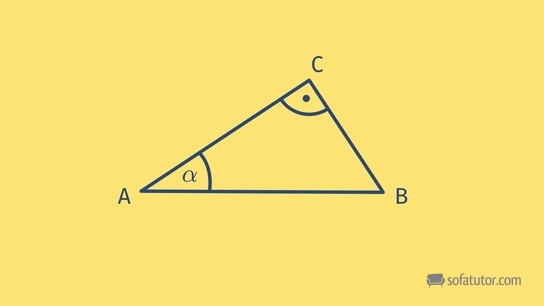
In der Trigonometrie, die ein Teil der Geometrie ist, beschäftigen wir uns mit rechtwinkligen Dreiecken. Fehlende Größen, also Winkel oder Seitenlängen, sollen berechnet werden. Ein solches rechtwinkliges Dreieck liegt vor, wenn einer der drei Winkel ![]() beträgt. Die Seite, die dem
beträgt. Die Seite, die dem ![]() -Winkel gegenüberliegt, wird als Hypotenuse bezeichnet. Die Seite gegenüber dem spitzen Winkel
-Winkel gegenüberliegt, wird als Hypotenuse bezeichnet. Die Seite gegenüber dem spitzen Winkel ![]() ist die Gegenkathete von
ist die Gegenkathete von ![]() und die dritte Seite, die an dem Winkel
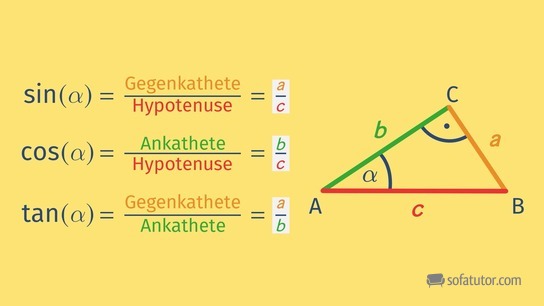
und die dritte Seite, die an dem Winkel ![]() anliegt, wird als Ankathete bezeichnet. Sinus, Cosinus und Tangens sind wie folgt definiert:
anliegt, wird als Ankathete bezeichnet. Sinus, Cosinus und Tangens sind wie folgt definiert:

![]()
![]()
![]()
Folgende Merksätze können dir helfen, dir die Formeln besser zu merken:
- Sinus und Cosinus enden auf „nus“, beide teilt man durch die HypoteNUSe.
- Für den Sinus: Sing(h) (Gegenkathete durch Hypotenuse)
- Für den Tangens: tanga (Gegenkathete durch Ankathete)
- Für den Cosinus bleibt somit nur noch, die Ankathete durch die Hypotenuse zu teilen.
Exkurs: Wir betrachten hier immer Dreiecke in der Ebene. Neben dieser ebenen Trigonometrie gibt es auch die sphärische Trigonometrie, die sich mit sphärischen Dreiecken beschäftigt.
Trigonometrie – Sätze und Zusammenhänge einfach erklärt
Ein wichtiger Zusammenhang zwischen den oben genannten drei Funktionen ist:
![]()
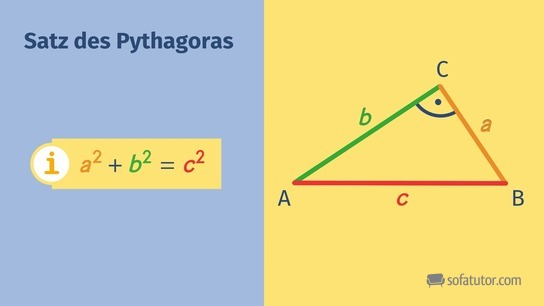
Der wohl bekannteste Satz im Zusammenhang mit rechtwinkligen Dreiecken ist der Satz des Pythagoras:
![]()
Die Summe der beiden Kathetenquadrate ist gleich groß wie das Quadrat der Hypotenuse.
Mithilfe des Einheitskreises und des Satzes des Pythagoras können wir einen weiteren Zusammenhang zwischen Sinus und Cosinus herleiten, den sogenannten trigonometrischen Pythagoras. In den Einheitskreis zeichnen wir ein rechtwinkliges Dreieck mit dem spitzen Winkel ![]() (siehe Abbildung). Der Einheitskreis hat einen Radius von
(siehe Abbildung). Der Einheitskreis hat einen Radius von ![]() und somit hat die Hypotenuse in diesem Dreieck die Länge
und somit hat die Hypotenuse in diesem Dreieck die Länge ![]() . Unter Verwendung der obigen Definitionen sehen wir:
. Unter Verwendung der obigen Definitionen sehen wir:

![]() entspricht der Länge der Gegenkathete und
entspricht der Länge der Gegenkathete und
![]() der Länge der Ankathete.
der Länge der Ankathete.
Einsetzen in den Satz des Pythagoras liefert:
![]()
da die Hypotenuse im Quadrat ![]() ist.
ist.
Des Weiteren besagt der Winkelsummensatz, dass du mithilfe eines gegebenen Winkels ![]() in einem rechtwinkligen Dreieck den gesuchten Winkel
in einem rechtwinkligen Dreieck den gesuchten Winkel ![]() berechnen kannst. Wir wissen, dass die Innenwinkelsumme eines Dreiecks
berechnen kannst. Wir wissen, dass die Innenwinkelsumme eines Dreiecks ![]() und ein Winkel im rechtwinkligen Dreieck
und ein Winkel im rechtwinkligen Dreieck ![]() beträgt. Somit können wir den Winkel
beträgt. Somit können wir den Winkel ![]() berechnen:
berechnen:
![]()
Weitere Zusammenhänge (Identitäten) sind:

Die zwei letzten Gleichungen werden auch Additionstheoreme genannt.
Es gibt jedoch sehr viel mehr Zusammenhänge, die hergeleitet oder in einer Formelsammlung nachgeschlagen werden können. Mithilfe dieser Identitäten können zum Beispiel Terme mit trigonometrischen Funktionen umgeformt und vereinfacht werden.
Trigonometrie – Winkelfunktionen, ihre Schaubilder und Werte
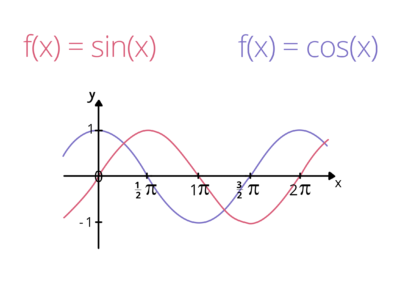
Die Abbildung zeigt den Verlauf der Sinus- und Cosinusfunktion.
Die Winkel sind hier im sogenannten Bogenmaß ![]() dargestellt, wobei gilt:
dargestellt, wobei gilt:
![]()
Es gibt einige charakteristische Werte, die du dir merken solltest, insbesondere für ![]() und
und ![]() . Diese sind in der folgenden Tabelle als Übersicht dargestellt.
. Diese sind in der folgenden Tabelle als Übersicht dargestellt.
| Winkel |
|||
|---|---|---|---|
| nicht definiert |
Beispiel gleichschenkliges Dreieck
Jetzt haben wir viel über rechtwinklige Dreiecke gelernt. Was macht man aber nun, wenn man einen Winkel oder eine Seite in einem gleichschenkligen Dreieck berechnen will?
Da gleichschenklige Dreiecke symmetrisch zur Höhe auf die Basis sind, können wir es entlang dieser in zwei kongruente rechtwinklige Dreiecke unterteilen. In diesen rechtwinkligen Dreiecken gelten dann alle Regeln von oben.

Trigonometrie – Exkurs: Ableitungen
In der Differenzialrechnung benötigt man die Ableitungen der trigonometrischen Funktionen:
![]()
![]()
![]()
Trigonometrie – Zusammenfassung
- Mithilfe der Trigonometrie können wir fehlende Größen in einem rechtwinkligen Dreieck berechnen.
- In einem rechtwinkligen Dreieck können wir folgende Beziehungen finden:


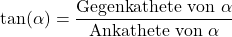
- Es gibt verschiedene Sätze, die uns Zusammenhänge zwischen den trigonometrischen Funktionen herstellen.
Häufig gestellte Fragen zum Thema Trigonometrie