Natürliche Zahlen – Definition und Beispiele
Erfahre, dass natürliche Zahlen alle positiven Zahlen sind, die zum Zählen verwendet werden – beginnend mit 1. Lerne, wie man sie vergleicht, addiert, multipliziert und sogar in Brüche umwandelt. Dies und weitere spannende Fakten erwarten dich im folgenden Text!
Inhaltsverzeichnis zum Thema Natürliche Zahlen
Die Zahlenmenge der natürlichen Zahlen – Definition
Die natürlichen Zahlen beginnen mit der Zahl ![]() . Jede natürliche Zahl hat einen Nachfolger, der um
. Jede natürliche Zahl hat einen Nachfolger, der um ![]() größer ist als die Zahl selbst. Das bedeutet, man startet mit der kleinsten natürlichen Zahl
größer ist als die Zahl selbst. Das bedeutet, man startet mit der kleinsten natürlichen Zahl ![]() und addiert
und addiert ![]() und so entsteht eine Menge von Zahlen. Dies ist die Menge der natürlichen Zahlen und wird mit dem Symbol
und so entsteht eine Menge von Zahlen. Dies ist die Menge der natürlichen Zahlen und wird mit dem Symbol ![]() bezeichnet. Um die Menge der natürlichen Zahlen mit ihren Elementen aufzuschreiben, werden die geschweiften Mengenklammern verwendet:
bezeichnet. Um die Menge der natürlichen Zahlen mit ihren Elementen aufzuschreiben, werden die geschweiften Mengenklammern verwendet:
![]()
Die drei Punkte am Ende der Mengenschreibweise bedeuten, dass die Menge in dem gleichen Muster fortgesetzt wird. Du kannst immer weiter ![]() rechnen und damit die nächstgrößere natürliche Zahl erhalten. Deswegen ist es nicht möglich, alle natürlichen Zahlen aufzuschreiben. Es gibt unendlich viele natürliche Zahlen.
rechnen und damit die nächstgrößere natürliche Zahl erhalten. Deswegen ist es nicht möglich, alle natürlichen Zahlen aufzuschreiben. Es gibt unendlich viele natürliche Zahlen.
Die Menge der natürlichen Zahlen wird auch als abzählbar unendlich bezeichnet, weil die Menge zwar unendlich groß ist, aber alle Elemente der Menge durchnummeriert bzw. gezählt werden können.
Es gibt unterschiedliche Sichtweisen, ob die Zahl ![]() zu den natürlichen Zahlen gehört oder nicht. Du findest in manchen Büchern daher das Zeichen
zu den natürlichen Zahlen gehört oder nicht. Du findest in manchen Büchern daher das Zeichen ![]() für die Menge der natürlichen Zahlen mit der Zahl
für die Menge der natürlichen Zahlen mit der Zahl ![]() . Es gibt aber auch die Variante, dass die
. Es gibt aber auch die Variante, dass die ![]() direkt zu
direkt zu ![]() gezählt wird.
gezählt wird.

Gerade und ungerade natürliche Zahlen
Die natürlichen Zahlen können in gerade und ungerade Zahlen unterteilt werden. Laut der Definition für gerade natürliche Zahlen sind dies alle natürlichen Zahlen, die durch ![]() teilbar sind. Die ungeraden Zahlen sind dann alle anderen natürlichen Zahlen, die nicht durch
teilbar sind. Die ungeraden Zahlen sind dann alle anderen natürlichen Zahlen, die nicht durch ![]() teilbar sind.
teilbar sind.
Natürliche Zahlen vergleichen
Beim Vergleichen von natürlichen Zahlen geht es darum, welche Zahl größer oder kleiner ist. Als mathematisches Symbol werden dafür ![]() und
und ![]() verwendet. Das bedeutet:
verwendet. Das bedeutet:
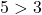 , man sagt „
, man sagt „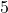 ist größer als
ist größer als 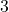 “.
“.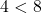 , man sagt „
, man sagt „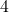 ist kleiner als
ist kleiner als 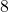 “.
“.
Um natürliche Zahlen zu vergleichen, gibt es verschiedene Möglichkeiten.
- Vergleichen zweier Zahlen nach Anzahl der Stellen: Eine Zahl mit mehr Stellen ist größer als eine mit weniger Stellen, zum Beispiel:
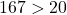 .
. - Vergleichen durch Subtraktion: Ergibt die Subtraktion der beiden Zahlen wieder eine natürliche Zahl, war der Minuend größer als der Subtrahend. Zum Beispiel:
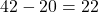 , also
, also 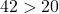
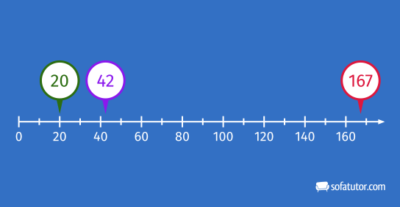
- Vergleichen von natürlichen Zahlen mithilfe des Zahlenstrahls: Am Zahlenstrahl werden die Zahlen der Größe nach angeordnet. Deswegen gilt:
Je weiter rechts eine Zahl auf dem Zahlenstrahl steht, desto größer ist sie. Je weiter links eine Zahl steht, desto kleiner ist sie.
Rechnen mit natürlichen Zahlen
Natürliche Zahlen können addiert und multipliziert werden.
Beispiele:
Natürliche Zahlen können auch subtrahiert und dividiert werden. Allerdings kann es dabei vorkommen, dass das Ergebnis der Rechnung keine natürliche Zahl mehr ist.
Beispiele:
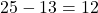 , hier ist das Ergebnis wieder eine natürliche Zahl.
, hier ist das Ergebnis wieder eine natürliche Zahl.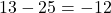 , hier ist das Ergebnis negativ, also keine natürliche Zahl.
, hier ist das Ergebnis negativ, also keine natürliche Zahl.
Gaußsche Summenformel
Es gibt eine Formel, mit der die Summe aller natürlichen Zahlen bis zu einer bestimmten Zahl ![]() berechnet werden kann. Die Formel hat der berühmte Mathematiker Carl Friedrich Gauß aufgestellt. Sie lautet:
berechnet werden kann. Die Formel hat der berühmte Mathematiker Carl Friedrich Gauß aufgestellt. Sie lautet:
Damit kann zum Beispiel ganz schnell die Summe aller natürlichen Zahlen bis ![]() berechnet werden. Anstelle einzeln zu summieren
berechnet werden. Anstelle einzeln zu summieren ![]() , rechnen wir:
, rechnen wir:
![]()
Brüche in natürliche Zahlen umwandeln
Entspricht der Wert eines Bruchs einer natürlichen Zahl, kann dieser Bruch auch als natürliche Zahl geschrieben werden. Dies ist dann der Fall, wenn im Nenner des gekürzten Bruchs eine ![]() steht. Ist der Bruch noch nicht gekürzt, erkennt man, dass der Wert einer natürlichen Zahl entspricht, wenn der Nenner ein Teiler des Zählers ist.
steht. Ist der Bruch noch nicht gekürzt, erkennt man, dass der Wert einer natürlichen Zahl entspricht, wenn der Nenner ein Teiler des Zählers ist.
Beispiel:
![]() oder
oder ![]()
Die Zahl ![]() ist eine natürliche Zahl.
ist eine natürliche Zahl.
Häufig gestellte Fragen zum Thema Natürliche Zahlen

