Zinsrechnung – Grundlagen, Formeln und Beispiele
Erfahre, wie Kapital mit Zinssatz über Zeit verzinst wird und was Zinseszins bedeutet. Verstehe wichtige Begriffe wie Kapital, Zinsen und Zinssatz.
Inhaltsverzeichnis zum Thema Zinsrechnung – Grundlagen, Formeln und Beispiele
Zinsrechnung einfach erklärt – Grundlagen und Formeln
Bei der Zinsrechnung geht es darum, dass ein Kapital mit einem bestimmten Zinssatz über einen festgelegten Zeitraum verzinst wird. Zusätzlich zum angelegten Kapital hast du nach Ablauf der Anlagedauer Zinsen auf deinem Konto.
Wichtige Begriffe sind also
- das Kapital
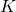 ,
, - die Zinsen
 und
und - der Zinssatz
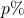 .
.
Die Zinsen ![]() für ein Jahr berechnen sich aus dem Produkt von Kapital
für ein Jahr berechnen sich aus dem Produkt von Kapital ![]() und Zinssatz
und Zinssatz ![]() :
:
![]()
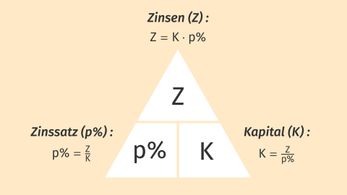
Die Zinsformel kannst du so umstellen, dass jede der Größen berechnet werden kann.
![]()
![]()
So kannst du neben den Zinsen auch den Zinssatz oder das Kapital berechnen, wenn die anderen beiden Größen gegeben sind.
Die Zinsrechnung kann als Anwendungsgebiet der Prozentrechnung verstanden werden. Dabei entsprechen sich die folgenden Größen:
| Prozentrechnung | Zinsrechnung |
|---|---|
| Grundwert |
Kapital |
| Prozentsatz |
Zinssatz |
| Prozentwert |
Zinsen |
Prozent- und Zinssatz werden in Prozent oder als Dezimalzahl angegeben.
Zinsrechnung mit gegebenem Zeitraum
Wie der Jahreszins berechnet wird, hast du bereits gelernt. Die Formel für die Zinsen eines Jahres lautet ![]() .
.
Wichtig bei der Betrachtung abweichender Zeiträume ist, dass du weißt, dass das Jahr als kaufmännisches Jahr betrachtet wird. Ein kaufmännisches Jahr hat ![]() Tage und jeder Monat
Tage und jeder Monat ![]() Tage.
Tage.

Wird ein Kapital kürzer als ein Jahr angelegt, berechnest du die Zinsen anteilig.
Möchtest du die Zinsen für einen Zeitraum von ![]() Monaten berechnen, multiplizierst du die Zinsformel mit dem Bruch
Monaten berechnen, multiplizierst du die Zinsformel mit dem Bruch ![]() . Die Variable
. Die Variable ![]() steht für die Anzahl der vollen Monate, in denen das Kapital verzinst wird. Da ein ganzes Jahr
steht für die Anzahl der vollen Monate, in denen das Kapital verzinst wird. Da ein ganzes Jahr ![]() Monate hat, teilen wir durch
Monate hat, teilen wir durch ![]() , um den Anteil zu ermitteln.
, um den Anteil zu ermitteln.
![]()
Ähnlich kannst du beim Berechnen der Tageszinsen vorgehen. Multipliziere die Formel zur Berechnung der Zinsen in diesem Fall mit dem Bruch ![]() . Die Variable
. Die Variable ![]() steht für die Anzahl der vollen Tage, die in dem Zeitraum liegen, über den das Kapital verzinst wird. Den Anteil erhalten wir, indem wir durch die
steht für die Anzahl der vollen Tage, die in dem Zeitraum liegen, über den das Kapital verzinst wird. Den Anteil erhalten wir, indem wir durch die ![]() Tage eines ganzen Jahres teilen.
Tage eines ganzen Jahres teilen.
![]()
Hier siehst du die Formel, mit denen du die Zinsen für genau ein Jahr, einen Monat oder einen Tag berechnen kannst zusammengefasst.

Zinsrechnung – Zinseszins
In der Regel werden Guthabenszinsen jährlich gezahlt. Das erkennst du auch daran, dass der Zinssatz häufig mit dem Zusatz p. a. angegeben wird, der für per annum (lat. für pro Jahr) steht.
Das bedeutet Folgendes: Ist ein Jahr vergangen, werden die berechneten Zinsen gutgeschrieben und erhöhen so das Kapital, das im Folgejahr verzinst wird. Das Kapital wird so jedes Jahr größer, wodurch auch die Zinsen mehr werden, da diese, neben dem Zinssatz, vom Kapital abhängen.
Stell dir vor, du legst zu Jahresbeginn ![]() € zu einem Zinssatz von
€ zu einem Zinssatz von ![]() an.
an.
Die Zinsen nach einem Jahr betragen entsprechend ![]() €
€ ![]() € und werden am Ende des Jahres gutgeschrieben.
€ und werden am Ende des Jahres gutgeschrieben.
Das Kapital ![]() nach einem Jahr beträgt
nach einem Jahr beträgt ![]() €. Zur Berechnung der Zinsen für das zweite Jahr dient nun dieses Kapital
€. Zur Berechnung der Zinsen für das zweite Jahr dient nun dieses Kapital ![]() als Grundlage:
als Grundlage:
![]() €
€ ![]() €
€
Diese Zinsen werden wiederum auf das Kapital addiert, nach zwei Jahren beträgt das Kapital demnach:
![]() €
€ ![]() €
€ ![]() €
€ ![]() €
€
Dieses Kapital wird nun im nächsten Jahr weiter verzinst.
Das Kapital wächst also jedes Jahr um den gleichen Faktor, wobei das Kapital selbst immer größer wird. Du kannst auch von exponentiellem Wachstum sprechen.
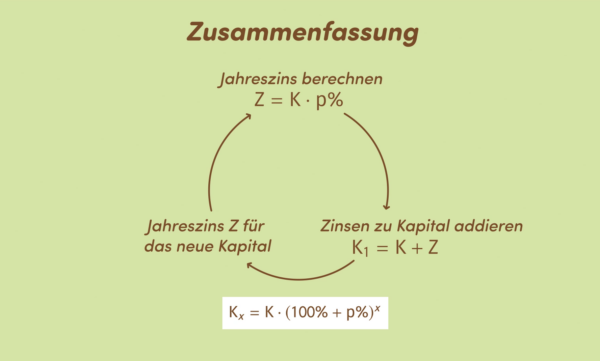
Allgemein kannst du bei einer Verzinsung über mehrere Jahre die folgende Formel verwenden:
![]()
Die Variable ![]() beschreibt die Anzahl der Jahre und entsprechend steht
beschreibt die Anzahl der Jahre und entsprechend steht ![]() für das Kapital nach
für das Kapital nach ![]() Jahren Verzinsung.
Jahren Verzinsung.
Beispiele zur Zinsrechnung
Im Folgenden sind einige Beispiele aufgeführt, an denen du die Zinsrechnung üben und dein Wissen testen kannst.
Beispiel 1
Dein Bruder legt für ein Jahr ![]() € zu einem Zinssatz von
€ zu einem Zinssatz von ![]() an. Du legst gleichzeitig
an. Du legst gleichzeitig ![]() € zu einem Zinssatz von
€ zu einem Zinssatz von ![]() an. Wer von euch hat am Ende des Jahres das höhere Guthaben?
an. Wer von euch hat am Ende des Jahres das höhere Guthaben?
Dein Bruder bekommt zu seinen Konditionen ![]() €
€ ![]() € Zinsen. Addierst du diese auf sein Kapital, hat er am Ende des Jahres ein Guthaben von
€ Zinsen. Addierst du diese auf sein Kapital, hat er am Ende des Jahres ein Guthaben von ![]() €.
€.
Du bekommst nach einem Jahr ![]() €
€ ![]() € Zinsen gutgeschrieben und hast mit
€ Zinsen gutgeschrieben und hast mit ![]() € das größere Guthaben, obwohl du weniger Zinsen erhalten hast.
€ das größere Guthaben, obwohl du weniger Zinsen erhalten hast.
Beispiel 2
Ein Sparkonto mit einem Guthaben von ![]() € und einer Verzinsung von
€ und einer Verzinsung von ![]() soll zum 01.07. aufgelöst werden. Wie viele Zinsen werden anteilig zur Auflösung gutgeschrieben?
soll zum 01.07. aufgelöst werden. Wie viele Zinsen werden anteilig zur Auflösung gutgeschrieben?
Um zu berechnen, wie viele Zinsen noch zum Guthaben hinzukommen, berechnest du die Zinsen für ein ganzes Jahr und multiplizierst diese anschließend mit dem Faktor ![]() , da das Geld noch für
, da das Geld noch für ![]() Monate angelegt war.
Monate angelegt war.
![]() €
€ ![]() €
€
Zur Auflösung werden noch ![]() € gutgeschrieben.
€ gutgeschrieben.
Beispiel 3
Ein Sparer legt zu Jahresbeginn ![]() € an. Nach Gutschrift der Zinsen nach einem Jahr beträgt sein Guthaben
€ an. Nach Gutschrift der Zinsen nach einem Jahr beträgt sein Guthaben ![]() €. Zu welchem Zinssatz
€. Zu welchem Zinssatz ![]() war das Geld angelegt?
war das Geld angelegt?
Um den Zinssatz zu berechnen, verwendest du die umgestellte Zinsformel:
![]()
Die Zinsen ![]() berechnest du, indem du das Startkapital vom Endkapital abziehst.
berechnest du, indem du das Startkapital vom Endkapital abziehst.
![]() €
€ ![]() €
€ ![]() €
€
Den Wert für ![]() kannst du dann mit dem Kapital
kannst du dann mit dem Kapital ![]() in die Formel einsetzen.
in die Formel einsetzen.
![]()
Das Kapital war also zu einem Zinssatz von ![]() angelegt.
angelegt.
Häufig gestellte Fragen zum Thema Zinsrechnung

