Exponentialfunktionen – einfach erklärt
Entdecke, wie Exponentialfunktionen exponentielles Wachstum oder Zerfall beschreiben. Lerne, wie der Wachstumsfaktor Einfluss nimmt und wie du den Funktionsgraph zeichnest. Bist du bereit für eine tiefergehende Einblick? Dann erfahre alles im folgenden Text!
Inhaltsverzeichnis zum Thema Exponentialfunktionen
Exponentialfunktion – Definition Mathe
Exponentialfunktionen sind Funktionen der Form ![]() . Sie beschreiben exponentielles Wachstum oder exponentiellen Zerfall. Bei Exponentialfunktionen steht die Variable, z. B.
. Sie beschreiben exponentielles Wachstum oder exponentiellen Zerfall. Bei Exponentialfunktionen steht die Variable, z. B. ![]() , immer im Exponenten. Der Parameter
, immer im Exponenten. Der Parameter ![]() ist die Basis von
ist die Basis von ![]() und wird als Wachstumsfaktor der Exponentialfunktion bezeichnet. Die Basis ist immer positiv. Der Parameter
und wird als Wachstumsfaktor der Exponentialfunktion bezeichnet. Die Basis ist immer positiv. Der Parameter ![]() ist der Anfangswert oder Streckfaktor der Exponentialfunktion.
ist der Anfangswert oder Streckfaktor der Exponentialfunktion.
Ist die Basis ![]() , handelt es sich nicht um eine Exponentialfunktion, sondern um eine parallel zur
, handelt es sich nicht um eine Exponentialfunktion, sondern um eine parallel zur ![]() -Achse verlaufende lineare Funktion. Egal welcher Wert für
-Achse verlaufende lineare Funktion. Egal welcher Wert für ![]() eingesetzt wird, der dazugehörige
eingesetzt wird, der dazugehörige ![]() -Wert ist gleich.
-Wert ist gleich.
![]()
![]()
![]()
![]()
![]()
Mithilfe von Exponentialfunktionen kann das exponentielle Wachstum von Viren oder Bakterien beschrieben werden. Aber auch die Halbwertszeit von radioaktiven Stoffen lässt sich mithilfe von Exponentialfunktionen bestimmen.
Exponentialfunktion – Beispiel: ![]()
Der Graph zur Funktion ![]() hat die folgende Form:
hat die folgende Form:
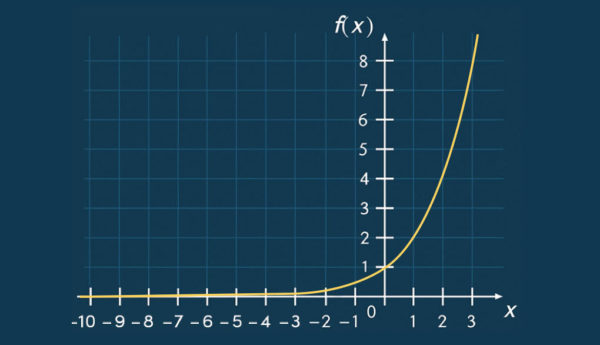
Der Graph einer Exponentialfunktion wird auch als Exponentialkurve bezeichnet.
Tritt ![]() nur im Exponenten einer Funktion auf, sprechen wir von einer reinen Exponentialfunktion. Existiert ein zusätzliches
nur im Exponenten einer Funktion auf, sprechen wir von einer reinen Exponentialfunktion. Existiert ein zusätzliches ![]() außerhalb des Exponenten, handelt es sich um eine verknüpfte Funktion.
außerhalb des Exponenten, handelt es sich um eine verknüpfte Funktion.
Beispiel: ![]()
Exponentialfunktion – allgemeine Formel
Die allgemeine Funktionsgleichung der Exponentialfunktion lautet:
![]() mit
mit ![]() und
und ![]()
Die Variable ![]() steht bei Exponentialfunktionen immer im Exponenten.
steht bei Exponentialfunktionen immer im Exponenten.
Beispiel: Ist die Basis ![]() , verdoppelt sich der Wert der Funktion mit jedem Schritt.
, verdoppelt sich der Wert der Funktion mit jedem Schritt.
Exponentialfunktion – Eigenschaften des Funktionsgraphen
Der Funktionsgraph einer Exponentialfunktion verläuft entweder streng monoton steigend (exponentielles Wachstum) oder streng monoton fallend (exponentieller Zerfall).
Der Parameter ![]() beeinflusst die Steigung des Graphen der Funktion. Dabei gilt:
beeinflusst die Steigung des Graphen der Funktion. Dabei gilt:
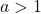 : streng monoton steigend
: streng monoton steigend
Je größer ist, desto steiler verläuft der Graph der Funktion.
ist, desto steiler verläuft der Graph der Funktion.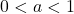 : streng monoton fallend
: streng monoton fallend
Je kleiner ist, desto schneller fällt der Graph der Funktion.
ist, desto schneller fällt der Graph der Funktion.
Der Parameter ![]() gibt bei
gibt bei ![]() den Schnittpunkt mit der
den Schnittpunkt mit der ![]() -Achse an, da
-Achse an, da ![]() .
.
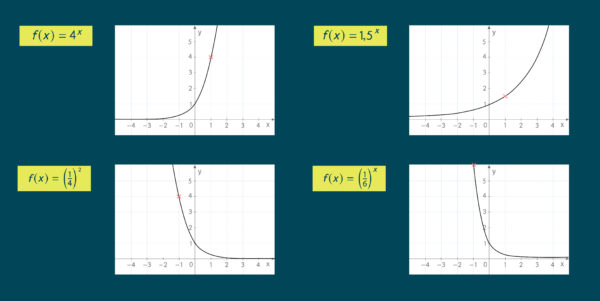
Für Exponentialfunktionen der Form ![]() gilt:
gilt:
- Wertebereich:
![Rendered by QuickLaTeX.com \mathbb{W} = ] 0 ; \infty [](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-3b7e831aaef747f87a99b83abb746df8_l3.png)
- Asymptote:
 -Achse
-Achse - Symmetrie: keine
- Nullstellen: keine
- Monotonie: streng monoton steigend für
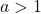 , streng monoton fallend für
, streng monoton fallend für 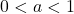
- Sie gehen immer durch die Punkt
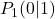 und
und 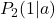 .
.
Exponentialfunktionen – verschieben, strecken, stauchen und spiegeln an der ![]() -Achse
-Achse
Neben dem Parameter ![]() können weitere Parameter den Verlauf des Funktionsgraphen einer Exponentialfunktion beeinflussen.
können weitere Parameter den Verlauf des Funktionsgraphen einer Exponentialfunktion beeinflussen.
Streckung, Stauchung und Spiegelung der Funktion
Der sogenannte Streckfaktor ![]() streckt, staucht oder spiegelt die Exponentialfunktion. Dabei gilt:
streckt, staucht oder spiegelt die Exponentialfunktion. Dabei gilt:
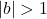 : Streckung des Graphen
: Streckung des Graphen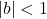 : Stauchung des Graphen
: Stauchung des Graphen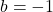 : Spiegelung des Graphen an der
: Spiegelung des Graphen an der  -Achse
-Achse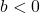 : Umkehrung des Monotonieverhaltens
: Umkehrung des Monotonieverhaltens
Für ![]() gilt:
gilt:
- Je größer
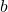 ist, desto weiter oben schneidet die Funktion die
ist, desto weiter oben schneidet die Funktion die  -Achse.
-Achse. 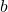 entspricht dem Schnittpunkt mit der
entspricht dem Schnittpunkt mit der  -Achse.
-Achse.
Für ![]() gilt:
gilt:
- Der Funktionsgraph ist an der
 -Achse gespiegelt.
-Achse gespiegelt. - Je kleiner
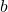 , desto weiter unten schneidet die Funktion die
, desto weiter unten schneidet die Funktion die  -Achse.
-Achse.
Eigenschaften
Für Exponentialfunktionen der Form ![]() gilt:
gilt:
- Wertebereich für
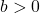 :
: ![Rendered by QuickLaTeX.com \mathbb{W} = ]0 ; \infty [](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-56fa9dd60ff6baa21c2f4dbfc9cd1d52_l3.png)
- Wertebereich für
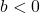 :
: ![Rendered by QuickLaTeX.com \mathbb{W} = ] - \infty ; 0 [](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-422ee54b9be72f530eef1227b2600c09_l3.png)
- Asymptote:
 -Achse
-Achse - Symmetrie: keine
- Nullstellen: keine
- Monotonie: streng monoton steigend für
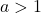 und
und 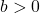 sowie
sowie 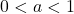 und
und 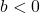 , streng monoton fallend für
, streng monoton fallend für 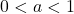 und
und 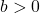 sowie
sowie 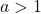 und
und 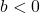
- Sie gehen immer durch die Punkt
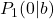 und
und 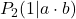 .
.
Beispiele
Der Graph der Funktion ![]() verläuft oberhalb der
verläuft oberhalb der ![]() -Achse und geht durch die Punkte
-Achse und geht durch die Punkte ![]() und
und ![]() .
.

Der Graph der Funktion ![]() verläuft ebenfalls oberhalb der
verläuft ebenfalls oberhalb der ![]() -Achse und geht durch die Punkte
-Achse und geht durch die Punkte ![]() und
und ![]() .
.
Verschieben in ![]() -Richtung
-Richtung
Durch die Verschiebungskonstante ![]() wird die Funktion um
wird die Funktion um ![]() Einheiten in
Einheiten in ![]() -Richtung verschoben. Dabei gilt:
-Richtung verschoben. Dabei gilt:
![]() : Verschiebung nach links
: Verschiebung nach links
![]() : Verschiebung nach rechts
: Verschiebung nach rechts
Die Funktionsgleichung lautet dann:
![]()
Die Verschiebung in Richtung der ![]() -Achse kann auch als Streckung oder Stauchung geschrieben werden. Durch die Potenzgesetze gilt:
-Achse kann auch als Streckung oder Stauchung geschrieben werden. Durch die Potenzgesetze gilt:
![]()
Die Verschiebung um ![]() Einheiten entspricht also einer Streckung mit dem Faktor
Einheiten entspricht also einer Streckung mit dem Faktor ![]() .
.
Verschiebung in ![]() -Richtung
-Richtung
Durch die Verschiebungskonstante ![]() wird die Funktion um
wird die Funktion um ![]() Einheiten in Richtung der
Einheiten in Richtung der ![]() -Achse verschoben. Dabei gilt:
-Achse verschoben. Dabei gilt:
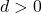 : Verschiebung nach oben
: Verschiebung nach oben : Verschiebung nach unten
: Verschiebung nach unten
Die Funktionsgleichung lautet dann:
![]()
Durch die Verschiebung nach oben oder unten verschiebt sich auch die Asymptote der Exponentialfunktion zu ![]() . Zudem kann durch die Verschiebung nach unten (bei positiven
. Zudem kann durch die Verschiebung nach unten (bei positiven ![]() ) eine Nullstelle entstehen. Bei der Verschiebung nach oben kann eine Nullstelle entstehen, wenn
) eine Nullstelle entstehen. Bei der Verschiebung nach oben kann eine Nullstelle entstehen, wenn ![]() negativ ist. Zudem ändert sich der Wertebereich der Funktion z. B. zu
negativ ist. Zudem ändert sich der Wertebereich der Funktion z. B. zu ![]() für
für ![]() .
.
Exponentialfunktion zeichnen
Wie lineare und quadratische Funktionen lassen sich auch Exponentialfunktionen mithilfe von Wertetabellen zeichnen. Um den Graphen einer Exponentialfunktion in ein Koordinatensystem zu zeichnen, erstellen wir also zunächst eine Wertetabelle.
Dafür wählen wir verschiedene ![]() -Werte und berechnen die zugehörigen
-Werte und berechnen die zugehörigen ![]() -Werte. Die so entstandenen Wertepaare können im Anschluss in ein Koordinatensystem eingetragen werden. Die Punkte werden dann zum Graphen der Funktion verbunden.
-Werte. Die so entstandenen Wertepaare können im Anschluss in ein Koordinatensystem eingetragen werden. Die Punkte werden dann zum Graphen der Funktion verbunden.
Beachte: Jede Exponentialfunktion besitzt eine waagrechte Asymptote bei ![]() , das heißt eine Linie, der sich der Graph nähert, sie jedoch nie berührt. Beim Einzeichnen musst du beachten, dass der Graph diese Linie nicht berührt oder schneidet.
, das heißt eine Linie, der sich der Graph nähert, sie jedoch nie berührt. Beim Einzeichnen musst du beachten, dass der Graph diese Linie nicht berührt oder schneidet.
Beispiel
Die folgende Funktion soll gezeichnet werden:
![]()
Da die Funktion die Form ![]() hat und
hat und ![]() positiv ist, liegt die Funktion oberhalb der
positiv ist, liegt die Funktion oberhalb der ![]() -Achse und hat eine Asymptote bei
-Achse und hat eine Asymptote bei ![]() . Zudem schneidet sie die
. Zudem schneidet sie die ![]() -Achse bei
-Achse bei ![]() . Weitere Punkte können wir mithilfe einer Wertetabelle berechnen:
. Weitere Punkte können wir mithilfe einer Wertetabelle berechnen:
Diese Punkte können wir nun in einem Koordinatensystem abtragen und zum Graphen der Funktion verbinden.
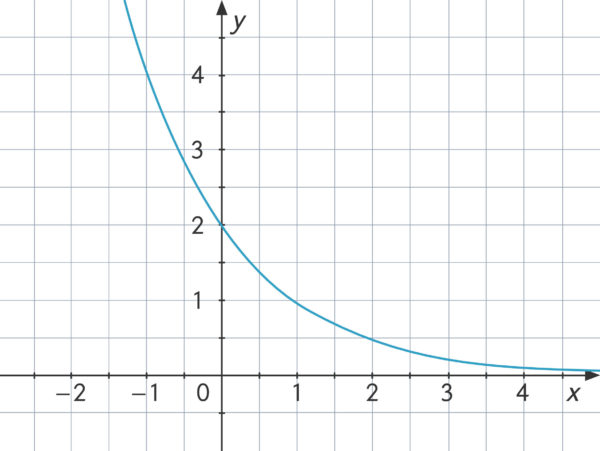
Exponentialfunktion – Funktionsgleichung bestimmen
Die Funktionsgleichung einer Exponentialfunktion lässt sich anhand von Punkten, die Teil der Lösungsmenge sind, oder anhand des Graphen der Funktion bestimmen.
Funktionsgleichung einer Exponentialfunktion aufstellen
Die Exponentialfunktionen der Form ![]() lassen sich mithilfe von einem Punkt bestimmen. Alle Funktionen dieser Form gehen durch den Punkt
lassen sich mithilfe von einem Punkt bestimmen. Alle Funktionen dieser Form gehen durch den Punkt ![]() , schneiden sich jedoch in keinem weiteren Punkt. Es muss also ein Punkt (außer
, schneiden sich jedoch in keinem weiteren Punkt. Es muss also ein Punkt (außer ![]() ) gegeben sein, um die Funktionsgleichung einer Exponentialfunktion der Form
) gegeben sein, um die Funktionsgleichung einer Exponentialfunktion der Form ![]() aufzustellen.
aufzustellen.
Kennen wir einen Punkt, der auf dem Graphen der Exponentialfunktion liegt, können wir den ![]() -Wert und den
-Wert und den ![]() -Wert in die Funktionsgleichung einsetzen und erhalten durch Äquivalenzumformung den Wert für
-Wert in die Funktionsgleichung einsetzen und erhalten durch Äquivalenzumformung den Wert für ![]() .
.
Besitzt die Funktion zusätzlich einen Streckfaktor ![]() , müssen zwei Punkte gegeben sein, um die Funktionsgleichung zu bestimmen. Wir erstellen zwei Gleichungen, indem wir die Koordinaten der beiden Punkte jeweils in die Funktionsgleichung einsetzen. Eine der beiden Gleichungen stellen wir im Anschluss nach
, müssen zwei Punkte gegeben sein, um die Funktionsgleichung zu bestimmen. Wir erstellen zwei Gleichungen, indem wir die Koordinaten der beiden Punkte jeweils in die Funktionsgleichung einsetzen. Eine der beiden Gleichungen stellen wir im Anschluss nach ![]() um und setzen den für
um und setzen den für ![]() erhaltenen Term in die andere Gleichung ein. Somit können wir
erhaltenen Term in die andere Gleichung ein. Somit können wir ![]() berechnen. Den Wert für
berechnen. Den Wert für ![]() setzen wir im Anschluss in eine der beiden Gleichungen ein, um
setzen wir im Anschluss in eine der beiden Gleichungen ein, um ![]() zu ermitteln.
zu ermitteln.
Besonders einfach ist das Bestimmen der Funktionsgleichung, wenn wir die Punkte mit den ![]() -Werten
-Werten ![]() und
und ![]() wählen. Für diese gilt:
wählen. Für diese gilt:
![]()
![]()
So können ![]() und
und ![]() sehr einfach bestimmt werden.
sehr einfach bestimmt werden.
Enthält die Gleichung zusätzlich noch einen dritten oder vierten Parameter (![]() und
und ![]() ), müssen entsprechend ein dritter und vierter Punkt oder andere zusätzliche Informationen, z. B. zur Asymptote der Funktion, gegeben sein, um die Funktionsgleichung zu bestimmen.
), müssen entsprechend ein dritter und vierter Punkt oder andere zusätzliche Informationen, z. B. zur Asymptote der Funktion, gegeben sein, um die Funktionsgleichung zu bestimmen.
Beispiel
Eine Exponentialfunktion der Form ![]() geht durch die Punkte
geht durch die Punkte ![]() und
und ![]() . Wie lautet die Funktionsgleichung?
. Wie lautet die Funktionsgleichung?
Zunächst setzen wir beide Punkte in die Funktion ein und erhalten die Gleichungen:
![]()
![]()
Nun können wir die erste Gleichung nach ![]() umstellen:
umstellen:
![]()
Diesen Term können wir nun für ![]() in die zweite Gleichung einsetzen und zusammenfassen:
in die zweite Gleichung einsetzen und zusammenfassen:
![]()
Nun können wir diese Gleichung nach ![]() auflösen und erhalten:
auflösen und erhalten:
![]()
Durch das Einsetzen von ![]() erhalten wir für
erhalten wir für ![]() :
:
![]()
Die Funktionsgleichung der Exponentialfunktion lautet:
![]()
Exponentialfunktion – Funktionsgleichung aus Graphen bestimmen
Ist uns der Graph einer Exponentialfunktion gegeben, können wir bereits an der Steigung erkennen, ob ![]() größer oder kleiner als
größer oder kleiner als ![]() ist. Verläuft der Graph oberhalb der
ist. Verläuft der Graph oberhalb der ![]() -Achse, ist für
-Achse, ist für ![]() die Funktion streng monoton steigend, für
die Funktion streng monoton steigend, für ![]() ist die Funktion streng monoton fallend. Geht der Graph zusätzlich durch den Punkt
ist die Funktion streng monoton fallend. Geht der Graph zusätzlich durch den Punkt ![]() , handelt es sich um eine Exponentialfunktion der Form
, handelt es sich um eine Exponentialfunktion der Form ![]() . Das bedeutet, wir wählen einen weiteren Punkt auf dem Graphen und können damit die Funktionsgleichung bestimmen.
. Das bedeutet, wir wählen einen weiteren Punkt auf dem Graphen und können damit die Funktionsgleichung bestimmen.
Schneidet der Graph die ![]() -Achse an einem anderen Punkt, können wir den Parameter
-Achse an einem anderen Punkt, können wir den Parameter ![]() der Exponentialfunktion ablesen. Bei
der Exponentialfunktion ablesen. Bei ![]() handelt es sich um den
handelt es sich um den ![]() -Achsenabschnitt. Mithilfe von
-Achsenabschnitt. Mithilfe von ![]() und einem weiteren Punkt, der auf dem Graphen liegt, lässt sich auch
und einem weiteren Punkt, der auf dem Graphen liegt, lässt sich auch ![]() ermitteln.
ermitteln.
Beispiel 1
Die Gleichung des folgenden Funktionsgraphen soll bestimmt werden:
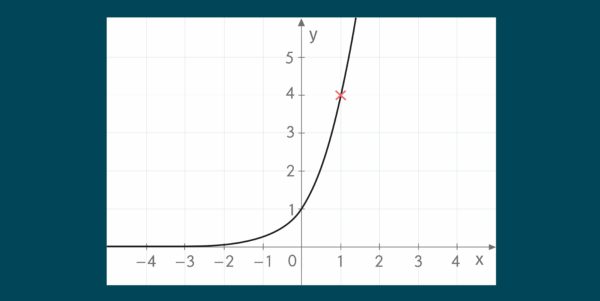
Da der Graph streng monoton steigt und oberhalb der ![]() -Achse verläuft, wissen wir, dass
-Achse verläuft, wissen wir, dass ![]() größer als
größer als ![]() ist. Zudem geht der Graph durch den Punkt
ist. Zudem geht der Graph durch den Punkt ![]() , somit handelt es sich um eine Funktion der Form
, somit handelt es sich um eine Funktion der Form ![]() . Um
. Um ![]() zu berechnen, wählen wir uns einen weiteren Punkt, der auf dem Graphen liegt und setzen die Koordinaten in die Funktionsgleichung ein:
zu berechnen, wählen wir uns einen weiteren Punkt, der auf dem Graphen liegt und setzen die Koordinaten in die Funktionsgleichung ein:
![]()
![]()
Die Funktionsgleichung lautet also:
![]()
Beispiel 2
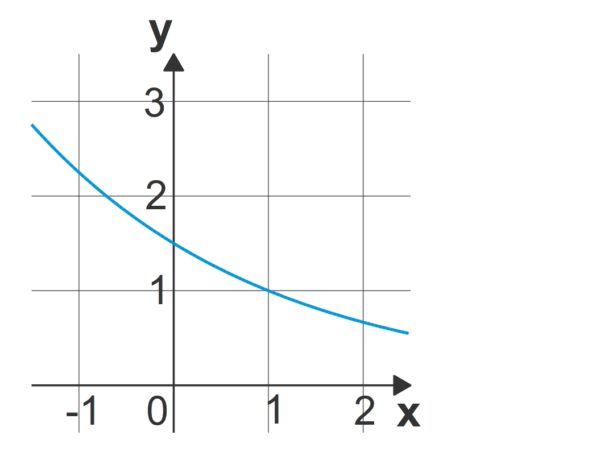
Die Gleichung des folgenden Funktionsgraphen soll bestimmt werden:
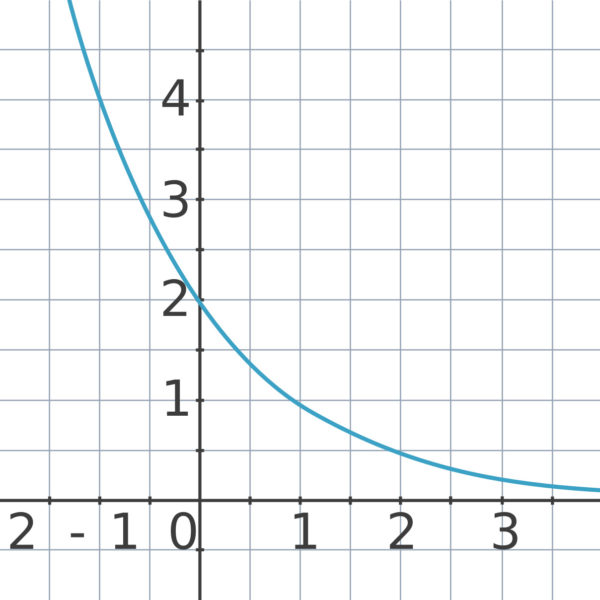
Da der Graph streng monoton fällt und oberhalb der ![]() -Achse verläuft, wissen wir, dass
-Achse verläuft, wissen wir, dass ![]() kleiner als
kleiner als ![]() ist. Zudem geht der Graph durch den Punkt
ist. Zudem geht der Graph durch den Punkt ![]() , somit handelt es sich um eine Funktion der Form
, somit handelt es sich um eine Funktion der Form ![]() . Um
. Um ![]() und
und ![]() zu berechnen, wählen wir uns zwei Punkte, die auf dem Graphen liegen, und setzen die Koordinaten in die Funktionsgleichung ein:
zu berechnen, wählen wir uns zwei Punkte, die auf dem Graphen liegen, und setzen die Koordinaten in die Funktionsgleichung ein:
![]()
![]()
Wir wissen, dass alle Funktionsgraphen von Funktionen der Form ![]() durch den Punkt
durch den Punkt ![]() gehen. Daraus folgt:
gehen. Daraus folgt:
![]()
Setzen wir diesen Wert für ![]() und die Koordinaten von
und die Koordinaten von ![]() für
für ![]() und
und ![]() in die Funktionsgleichung ein, erhalten wir für
in die Funktionsgleichung ein, erhalten wir für ![]() :
:
![]()
Die Funktionsgleichung lautet also:
![]()
Die natürliche Exponentialfunktion
Die ![]() -Funktion oder natürliche Exponentialfunktion ist ein Spezialfall der Exponentialfunktion. Dabei bildet die eulersche Zahl
-Funktion oder natürliche Exponentialfunktion ist ein Spezialfall der Exponentialfunktion. Dabei bildet die eulersche Zahl ![]() die Basis der Funktion:
die Basis der Funktion:
![]() mit
mit ![]()
Die Steigung der ![]() -Funktion entspricht in jedem Punkt genau ihrem Funktionswert. Daher ist die Ableitung von
-Funktion entspricht in jedem Punkt genau ihrem Funktionswert. Daher ist die Ableitung von ![]() ebenfalls
ebenfalls ![]() .
.
Umkehrfunktion von Exponentialfunktionen
Die Umkehrfunktion der Exponentialfunktion ist die Logarithmusfunktion:
![]()
Diese wird benötigt, wenn die Exponentialfunktion nach ![]() aufgelöst werden soll. Die Umkehrfunktion der
aufgelöst werden soll. Die Umkehrfunktion der ![]() -Funktion ist die
-Funktion ist die ![]() -Funktion (natürlicher Logarithmus
-Funktion (natürlicher Logarithmus ![]() ).
).
Beispiel
![]()
![]()
Exponentialfunktion – Ableitung
Für das Ableiten von Exponentialfunktionen gilt:
![]()
![]()
Um eine Exponentialfunktion abzuleiten, kannst du diese zunächst umschreiben als:
![]()
Die rechte Seite lässt sich nun einfach durch die Kettenregel ableiten.
Beispiel
![]()
![]()
Exponentialfunktion integrieren
Exponentialfunktion – Kurvendiskussion Beispiel
An der folgenden Exponentialfunktion soll eine Kurvendiskussion durchgeführt werden:
![]()
Dabei handelt es sich nicht um eine reine Exponentialfunktion, sondern um eine verknüpfte Funktion, da die Variable ![]() nicht nur im Exponenten steht.
nicht nur im Exponenten steht.
Exponentialfunktion – Definitionsbereich
Der Definitionsbereich umfasst alle Zahlen, die für ![]() in die Funktionsgleichung eingesetzt werden können. Bei Exponentialfunktionen sind das alle reellen Zahlen. Es gilt also:
in die Funktionsgleichung eingesetzt werden können. Bei Exponentialfunktionen sind das alle reellen Zahlen. Es gilt also:
![]()
Beispiel
Da für ![]() alle reellen Zahlen in die Gleichung eingesetzt werden können, ist der Definitionsbereich der Funktion:
alle reellen Zahlen in die Gleichung eingesetzt werden können, ist der Definitionsbereich der Funktion:
![]()
Exponentialfunktionen – ![]() -Achsenabschnitt
-Achsenabschnitt
Exponentialfunktionen schneiden die ![]() -Achse maximal an einer Stelle. Setzen wir für
-Achse maximal an einer Stelle. Setzen wir für ![]() in der Gleichung null ein, dann erhalten wir den
in der Gleichung null ein, dann erhalten wir den ![]() -Achsenabschnitt.
-Achsenabschnitt.
Beispiel
![]()
Der Schnittpunkt mit der ![]() -Achse liegt bei
-Achse liegt bei ![]() .
.
Exponentialfunktion – Nullstellen
Als Nullstellen werden die Schnittpunkte von Funktionen mit der ![]() -Achse bezeichnet. Exponentialfunktionen der Form
-Achse bezeichnet. Exponentialfunktionen der Form ![]() besitzen keine Nullstellen. Sie nähern sich der
besitzen keine Nullstellen. Sie nähern sich der ![]() -Achse lediglich an, schneiden diese jedoch nie. Ist die Funktion durch den Parameter
-Achse lediglich an, schneiden diese jedoch nie. Ist die Funktion durch den Parameter ![]() nach oben oder unten verschoben oder mit einer anderen Funktion verknüpft, kann die Funktion eine Nullstelle besitzen. Diese erhalten wir, indem wir den Funktionswert
nach oben oder unten verschoben oder mit einer anderen Funktion verknüpft, kann die Funktion eine Nullstelle besitzen. Diese erhalten wir, indem wir den Funktionswert ![]() setzen.
setzen.
Beispiel
![]()
Da es sich um ein Produkt handelt, gilt der Satz vom Nullprodukt: Ist ein Faktor null, ist das Produkt ebenfalls null.
Wir müssen also schauen, für welche Zahlen einer der beiden Faktoren gleich null wird:
![]()
![]()
Egal welche Zahl im Exponenten steht, der zweite Faktor wird niemals null, denn Exponentialfunktionen haben für sich keine Nullstelle. Somit ergibt sich für diese Funktion eine Nullstelle bei ![]() .
.
Exponentialfunktionen – Grenzwerte
Grenzwerte werden bestimmt, indem wir das Verhalten der Funktion betrachten, wenn ![]() gegen plus bzw. gegen minus unendlich läuft. Bei Exponentialfunktionen mit
gegen plus bzw. gegen minus unendlich läuft. Bei Exponentialfunktionen mit ![]() gilt:
gilt:
Grenzwert gegen plus unendlich:
 für
für 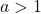
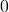 für
für 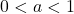
Grenzwert gegen minus unendlich:
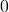 für
für 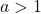
 für
für 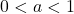
Beispiel
Im Unendlichen dominiert stets der Teil der Funktion, der die Exponentialfunktion enthält. Den quadratischen Teil können wir in diesem Beispiel vernachlässigen.
![]()
![]()
Für ![]() gegen
gegen ![]() nähert sich der Graph der Funktion also asymptotisch der
nähert sich der Graph der Funktion also asymptotisch der ![]() -Achse. Für
-Achse. Für ![]() gegen
gegen ![]() gehen die Funktionswerte gegen
gehen die Funktionswerte gegen ![]() .
.
Exponentialfunktion – Symmetrie
Für achsensymmetrische Funktionen gilt:
![]()
Für punktsymmetrische Funktionen gilt:
![]()
Keine der beiden Bedingungen ist für reine Exponentialfunktionen erfüllt. Reine Exponentialfunktionen sind weder achsen- noch punktsymmetrisch.
Beispiel
Achsensymmetrie: ![]()
Punktsymmetrie: ![]()
Die Funktion ist weder achsen- noch punktsymmetrisch.
Exponentialfunktion – Hoch- und Tiefpunkte
Reine Exponentialfunktionen haben weder Hoch- noch Tiefpunkte. Als Verknüpfung mit anderen Funktionen können Extrema auftreten.
Zur Berechnung der Extrempunkte werden die ersten zwei Ableitungen der Funktion benötigt.
Beispiel
Zunächst berechnen wir die ersten beiden Ableitungen:
![]()
![]()
![]()
Wie genau du ![]() -Funktionen ableitest, lernst du im Text
-Funktionen ableitest, lernst du im Text ![]() -Funktionen ableiten. Zunächst überprüfen wir die notwendige Bedingung. Dafür setzen wir die erste Ableitung gleich null:
-Funktionen ableiten. Zunächst überprüfen wir die notwendige Bedingung. Dafür setzen wir die erste Ableitung gleich null:
![]()
Daraus ergeben sich die Nullstellen ![]() und
und ![]() . Nun müssen wir die hinreichende Bedingung prüfen. Dafür setzen wir die Nullstellen in die zweite Ableitung ein und überprüfen, ob sie an diesen Stellen ungleich null ist.
. Nun müssen wir die hinreichende Bedingung prüfen. Dafür setzen wir die Nullstellen in die zweite Ableitung ein und überprüfen, ob sie an diesen Stellen ungleich null ist.
![]()
![]()
![]()
Um die Extrempunkte zu erhalten, benötigen wir die dazugehörigen ![]() -Werte. Dafür setzen wir die
-Werte. Dafür setzen wir die ![]() -Werte in die Gleichung ein und erhalten die Extrempunkte:
-Werte in die Gleichung ein und erhalten die Extrempunkte:
![]()
![]()
Der Graph dieser Funktion besitzt einen Tiefpunkt bei ![]() und einen Hochpunkt bei
und einen Hochpunkt bei ![]() .
.
Exponentialfunktion – Wendepunkte
Reine Exponentialfunktionen besitzen keine Wendepunkte. Als Verknüpfung mit anderen Funktionen können Wendepunkte auftreten.
Zur Berechnung der Wendepunkte werden die ersten drei Ableitungen der Funktion benötigt.
Beispiel
Zunächst berechnen wir die dritte Ableitung der Funktion:
![]()
Nun setzen wir die zweite Ableitung gleich null:
![]()
Wir erhalten die Nullstellen:
![]()
![]()
Nun müssen wir die hinreichende Bedingung prüfen. Dafür setzen wir die Nullstellen in die dritte Ableitung ein und überprüfen, ob sie an diesen Stellen ungleich null ist.
![]()
![]()
![]()
Bei beiden Stellen handelt es sich also um Wendepunkte. Um die dazugehörigen ![]() -Werte zu berechnen, setzen wir die
-Werte zu berechnen, setzen wir die ![]() -Werte in die Ausgangsfunktion ein:
-Werte in die Ausgangsfunktion ein:
![]()
![]()
Der Graph dieser Funktion besitzt zwei Wendepunkte bei ![]() und bei
und bei ![]() .
.
Exponentialfunktion – Wertebereich
Der Wertebereich umfasst alle für ![]() möglichen Werte. Bei einer Exponentialfunktion mit positivem
möglichen Werte. Bei einer Exponentialfunktion mit positivem ![]() liegt der Wertebereich zwischen der Asymptote der Funktion und plus unendlich. Bei einer Exponentialfunktion mit einem negativen
liegt der Wertebereich zwischen der Asymptote der Funktion und plus unendlich. Bei einer Exponentialfunktion mit einem negativen ![]() liegt der Wertebereich zwischen minus unendlich und der Asymptote. Durch den Verschiebungsfaktor
liegt der Wertebereich zwischen minus unendlich und der Asymptote. Durch den Verschiebungsfaktor ![]() oder das Verknüpfen der Funktion kann sich dieser Wertebereich ändern.
oder das Verknüpfen der Funktion kann sich dieser Wertebereich ändern.
Beispiel
Die Funktion nähert sich gegen ![]() gegen null, besitzt jedoch vorher einen Tiefpunkt bei
gegen null, besitzt jedoch vorher einen Tiefpunkt bei ![]() . Somit umfasst der Wertbereich alle Zahlen größer gleich null:
. Somit umfasst der Wertbereich alle Zahlen größer gleich null:
![]()
Funktionsgraph zeichnen
Mithilfe einer Wertetabelle und den aus der Kurvendiskussion bekannten Punkten kann nun der Funktionsgraph der Exponentialfunktion gezeichnet werden.
Beispiel
Der Graph der Funktion ![]() sieht folgendermaßen aus:
sieht folgendermaßen aus:
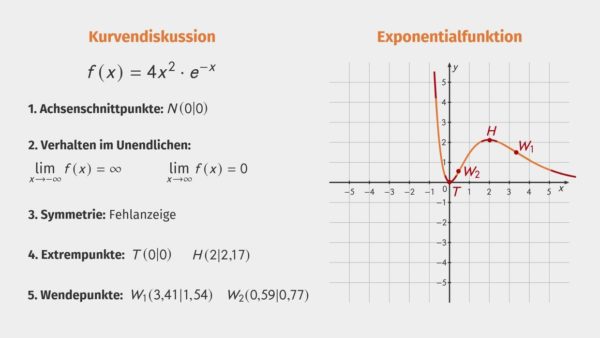
Exponentialfunktion aufstellen
Ist eine Textaufgabe gegeben, aus der eine Exponentialfunktion aufgestellt werden soll, ist es zunächst wichtig, die gegebenen Werte den entsprechenden Parametern zuzuordnen.
Beispiel – exponentielles Wachstum
Aufgabe
Emma legt ![]() Euro zu einem Zinssatz von
Euro zu einem Zinssatz von ![]() an. Wie lautet die Exponentialgleichung, die das Zinswachstum beschreibt? Wie viel Geld liegt nach
an. Wie lautet die Exponentialgleichung, die das Zinswachstum beschreibt? Wie viel Geld liegt nach ![]() Jahren auf dem Konto?
Jahren auf dem Konto?
Lösung
Zunächst müssen die angegebenen Werte den entsprechenden Parametern zugeordnet werden. Bei ![]() handelt es sich um den Anfangswert. Daraus folgt:
handelt es sich um den Anfangswert. Daraus folgt:
![]()
Der Parameter ![]() ist der Wachstumsfaktor. Diesen berechnen wir als:
ist der Wachstumsfaktor. Diesen berechnen wir als:
![]()
Setzen wir beide Werte in die Formel ein, erhalten wir die Exponentialfunktion:
![]()
Um zu berechnen, wie viel Geld nach ![]() Jahren auf dem Konto liegt, müssen wir für
Jahren auf dem Konto liegt, müssen wir für ![]() die
die ![]() einsetzen und erhalten:
einsetzen und erhalten:
![]()
Antwortsatz
Die Exponentialfunktion zur Aufgabe lautet ![]() und nach
und nach ![]() Jahren befinden sich
Jahren befinden sich ![]() Euro auf dem Konto.
Euro auf dem Konto.
Beispiel – exponentieller Zerfall
Aufgabe
Der Baumbestand eines Walds nimmt jährlich um ![]() ab. Zu Beginn der Messung betrug die Waldfläche
ab. Zu Beginn der Messung betrug die Waldfläche ![]() Hektar. Wie lautet die Exponentialgleichung, die die verbleibende Waldfläche nach
Hektar. Wie lautet die Exponentialgleichung, die die verbleibende Waldfläche nach ![]() Jahren beschreibt? Wie groß ist die Waldfläche
Jahren beschreibt? Wie groß ist die Waldfläche ![]() Jahre nach Beginn der Messung?
Jahre nach Beginn der Messung?
Lösung
Der Anfangswert ![]() ist:
ist:
![]()
Der Wachstumsfaktor ![]() berechnet sich als:
berechnet sich als:
![]()
Es wird minusgerechnet, da es sich um eine Abnahme handelt.
Setzen wir beide Werte in die Formel ein, erhalten wir die Exponentialfunktion:
![]()
Um die Waldfläche ![]() Jahre nach Beginn der Messung zu berechnen, setzen wir für
Jahre nach Beginn der Messung zu berechnen, setzen wir für ![]() die
die ![]() ein und erhalten den Wert:
ein und erhalten den Wert:
![]()
Antwortsatz
Die Exponentialfunktion zur Aufgabe lautet ![]() und nach
und nach ![]() Jahren beträgt die Waldfläche noch
Jahren beträgt die Waldfläche noch ![]() Hektar.
Hektar.
Häufig gestellte Fragen zum Thema Exponentialfunktionen

