Kreiszahl Pi – Definition, Anwendung und Beispiele

Die Kreiszahl Pi () ist eine wichtige mathematische Konstante für die Berechnung von Kreisen und Kugeln. Sie ist irrational und unendlich. Entdecke ihre Anwendung in der Mathematik und Physik! Dies und vieles mehr findest du im folgenden Text.

Kreiszahl Pi im Überblick

Kreiszahl Pi im Überblick

  • Die Kreiszahl Pi (\pi) ist eine Konstante mit dem näherungsweisen Wert {\pi \approx 3,\!142}.

  • Die Kreiszahl Pi (\pi) hat unendlich viele Nachkommastellen, sie ist also eine irrationale Zahl.

  • Die Kreiszahl Pi (\pi) wird für viele Berechnungen in Mathe und Physik benötigt, beispielsweise bei Kreis- oder Kugelberechnungen.

Kreiszahl Pi Video

Quelle sofatutor.com

Kreiszahl Pi – Definition

Die Kreiszahl mit dem Symbol \pi ist eine wichtige Konstante, die einem immer wieder in Mathe begegnet, insbesondere bei den Berechnungen von Kreisen und Kugeln.

Wir können den Wert der Kreiszahl nicht exakt bestimmen. Je mehr Nachkommastellen wir in einer Rechnung verwenden, desto exakter ist das Ergebnis. Es gilt:

\pi = 3,\!14159265358979\dots

Da \pi eine nicht periodische Dezimalzahl mit unendlich vielen Nachkommastellen ist, kann sie nicht als Bruch von zwei ganzen Zahlen dargestellt werden und gehört damit zu den irrationalen Zahlen. Außerdem hat \pi keine Einheit. Die Kreiszahl setzt den Umfang U und Durchmesser d eines Kreises ins Verhältnis:

\pi = \dfrac{U}{d}

Kreiszahl Pi berechnen

Ausgehend von der Definition als Quotient aus Umfang und Durchmesser eines Kreises, lässt sich \pi näherungsweise berechnen. Dazu messen wir bei verschiedenen Kreisen Umfang und Durchmesser und bilden den Quotienten:

Kreiszahl Pi: Kreise mit verschiedenen Durchmessern

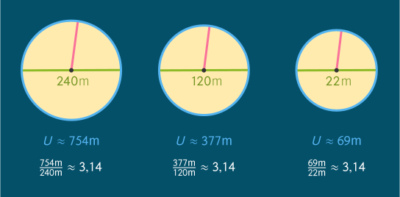
Wir erhalten in allen drei Fällen eine gute Näherung der Zahl \pi auf zwei Nachkommastellen.

Kreiszahl Pi – Geschichte

Schon früh wurde das Verhältnis vom Umfang eines Rads zu seinem Durchmesser benötigt, um ein solches herzustellen. Um 250 v. Chr. begann Archimedes, die Kreiszahl Pi näherungsweise zu bestimmen. Er zeichnete einen Einheitskreis mit Radius r = 1 (orange) und jeweils ein regelmäßiges Vieleck in (lila) und um (grün) diesen Einheitskreis. Dabei begann er mit einem Sechseck.

Annäherung an Pi mithilfe von Vierecken

Die Umfänge der regelmäßigen Vielecke können leicht durch Addition der Seitenlängen berechnet werden. Die Umfangslänge des Kreises muss dabei zwischen der des inneren und äußeren Vielecks liegen. Für eine immer genauere Abschätzung musste er lediglich die Anzahl der Ecken der Vielecke erhöhen. Dadurch erhielt er Grenzen, in denen die Zahl \pi liegen musste. Er bestimmte die Zahl \pi mithilfe eines 96-Ecks bis auf zwei Nachkommastellen genau.

Gottfried Leibniz konnte mit der Leibniz-Reihe mehr als 35 Nachkommastellen von \pi berechnen.

Heute können mithilfe von Computern über 62 Billionen Nachkommastellen von \pi bestimmt werden.

Kreiszahl Pi – Herleitung

Eine einfache Herleitung der Kreiszahl \pi sieht wie folgt aus:

Zeichne einen Kreis mit Durchmesser d= 1~\text{cm} und messe möglichst genau den Umfang, z. B. mithilfe einer Schnur. Die Schnur wird ungefähr 3,\!14~\text{cm} lang sein. Dann nutzt du die Formel, um \pi zu berechnen:
\pi = \dfrac{U}{d}

Wird hier für den Durchmesser d=1~\text{cm} eingesetzt, erhalten wir:
\pi = \dfrac{U}{d} = \dfrac{3,\!14~\text{cm}}{1~\text{cm}} = 3,\!14
Also ist \pi \approx 3,\!14.

Anwendung der Kreiszahl Pi

Die Kreiszahl \pi findet sich z. B. in den Formeln zur Berechnung von Umfang U oder Flächeninhalt A von Kreisen oder auch Umfang, Oberfläche und Volumen von Kugeln wieder. Folgende Tabelle gibt einen Überblick über häufig benutzte Formeln mit der Zahl \pi:

Kreis Kugel
Umfang U U = \pi \cdot d U = \pi \cdot d
Fläche A bzw. Oberfläche O A= \pi \cdot r^2 {O = 4 \pi \cdot r^2 = \pi \cdot d^2}
Volumen V – {V = \frac{4}{3} \pi \cdot r^3}

Berechnungen mit der Kreiszahl Pi – Beispiele

Wir wollen Umfang und Flächeninhalt eines Kreises mit Radius r= 3~\text{cm} bestimmen. Dazu brauchen wir die Formeln aus der Tabelle und setzen den Radius bzw. Durchmesser d=2r ein:
U = \pi \cdot d= \pi \cdot 2\cdot 3~\text{cm} \approx 18,\!85~\text{cm}
A = \pi \cdot r^2 = \pi \cdot (3 ~\text{cm})^2 \approx 28,\!27~\text{cm}^2

Häufig gestellte Fragen zum Thema Kreiszahl Pi

Die Kreiszahl \pi ist eine mathematische Konstante mit großer Bedeutung. Sie setzt den Umfang und Durchmesser eines Kreises ins Verhältnis und ist in vielen Formeln enthalten, beispielsweise in Kreisberechnungen.

Die Kreiszahl Pi beginnt wie folgt: \pi = 3,\!141 \dots. Sie hat unendlich viele Nachkommastellen.

Die Zahl \pi ist eine Konstante und hat den Wert \pi = 3,\!141 \dots.

Nein, \pi ist keine rationale Zahl, da sie eine nicht periodische Dezimalzahl mit unendlich vielen Nachkommastellen ist und somit nicht als Bruch dargestellt werden kann. Sie ist eine irrationale Zahl und gehört damit zu den reellen Zahlen.

Ja, \pi ist eine irrationale Zahl, da sie unendlich viele Nachkommastellen hat, und gehört daher zu den reellen Zahlen.

Die Kreiszahl \pi ist eine Konstante und setzt den Umfang und Durchmesser eines Kreises ins Verhältnis. Sie wird für viele Berechnungen in der Mathematik oder Physik benötigt.

Erfunden hat die Zahl \pi niemand. Sie wurde von Archimedes entdeckt, der die Idee hatte, das Verhältnis von Umfang zu Durchmesser durch ein Näherungsverfahren herauszufinden.

Die Zahl \pi hat unendlich viele Nachkommastellen.

Die Kreiszahl \pi ist ungefähr 3,\!142.

Die Kreiszahl \pi ist eine Konstante, die du dir merken solltest: \pi \approx 3,\!14. Du kannst sie dir einfach selbst herleiten, indem du einen Kreis mit Durchmesser d=1~\text{cm} zeichnest, den Umfang misst und beides in die Formel \pi = \frac{U}{d} einsetzt. Es wird \pi \approx 3,\!14 herauskommen.

Die Zahl \pi hat unendlich viele Nachkommastellen.

Die Kreiszahl \pi setzt den Umfang und Durchmesser eines Kreises ins Verhältnis und ist unabhängig von der Größe des Kreises. Sie ist also naturgegeben.

Die Kreiszahl \pi wird benötigt, um Umfang oder Flächeninhalt eines Kreises sowie Umfang, Oberfläche und Volumen einer Kugel auszurechnen.

Leave A Comment

Alle Artikel aus dem Fach Mathematik