Matrizen – Definition, Eigenschaften und Anwendungen
Eine Matrix ist ein rechteckiges Schema von Zahlen, das verschiedene mathematische Operationen ermöglicht. Erfahre mehr über Matrizen, ihre Eigenschaften wie Ordnung und Typen, Rechenregeln und Anwendungen wie Flächenberechnung und lineare Gleichungssysteme.
Inhaltsverzeichnis zum Thema Matrizen
Matrizen im Überblick
Matrizen – Definition und Eigenschaften
Eine Matrix ist ein rechteckiges Schema von Zahlen, ähnlich wie eine Tabelle, ein magisches Quadrat oder ein ausgefülltes Sudoku. Anders als mit Tabellen kann mit Matrizen in der Mathematik direkt gerechnet werden. Dabei gelten ähnliche Rechenregel wie beim Rechnen mit Zahlen. Matrizen werden zum Beispiel verwendet, um lineare Gleichungssysteme zu lösen, um Vektoren auf lineare Unabhängigkeit zu testen oder um das Volumen eines Parallelotops zu berechnen.
Definition der Matrix
In der Mathematik ist eine Matrix ein rechteckiges Schema von Zahlen, das von runden Klammern umschlossen wird. Die Zahlen in der Matrix nennt man die Einträge der Matrix.
Matrizen benennt man in der Regel durch lateinische Großbuchstaben: ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() , …,
, …, ![]() ,
, ![]() usw. Die Einträge der Matrix bezeichnet man mit den zugehörigen Kleinbuchstaben. Hier ist ein Beispiel:
usw. Die Einträge der Matrix bezeichnet man mit den zugehörigen Kleinbuchstaben. Hier ist ein Beispiel:

Alle Zahlen, die in einer Matrix vertikal untereinander stehen, bilden zusammen jeweils eine Spalte der Matrix. Alle Zahlen, die horizontal nebeneinander stehen, bilden jeweils eine Zeile der Matrix.
In unserem Beispiel oben ist
![]()
die zweite Zeile der Matrix ![]() und
und
![]()
die dritte Spalte von ![]() .
.
Die Ordnung einer Matrix gibt an, wie viele Zeilen und Spalten die Matrix hat. Die erste Zahl benennt die Anzahl der Zeilen, die zweite Zahl die Anzahl der Spalten. Die Matrix ![]() in unserem Beispiel hat
in unserem Beispiel hat ![]() Zeilen und
Zeilen und ![]() Spalten, daher ist
Spalten, daher ist ![]() eine
eine ![]() -Matrix.
-Matrix.
Will man die Anzahl der Zeilen und Spalten nicht ausdrücklich festlegen, verwendet man meistens die Variablen ![]() für die Anzahl der Zeilen und
für die Anzahl der Zeilen und ![]() für die Anzahl der Spalten. Eine
für die Anzahl der Spalten. Eine ![]() –Matrix hat also
–Matrix hat also ![]() Zeilen und
Zeilen und ![]() Spalten.
Spalten.
Um die Einträge in einer Matrix benennen zu können, verwendet man einen Doppelindex ![]() . Die Variablen
. Die Variablen ![]() und
und ![]() sind Platzhalter für Zahlen, die die Zeile und die Spalte der Matrix bezeichnen. Der Doppelindex wird als zwei einzelne Zahlen gelesen, geschrieben wird er ohne Kommatrennung. Den Doppelindex
sind Platzhalter für Zahlen, die die Zeile und die Spalte der Matrix bezeichnen. Der Doppelindex wird als zwei einzelne Zahlen gelesen, geschrieben wird er ohne Kommatrennung. Den Doppelindex ![]() lesen wir beispielsweise als „zwei drei“
lesen wir beispielsweise als „zwei drei“
Die beiden Zahlen des Doppelindex ![]() geben an, an welcher Stelle in der Matrix der Eintrag steht. Die erste Zahl benennt die Zeile, die zweite Zahl die Spalte: Der Eintrag
geben an, an welcher Stelle in der Matrix der Eintrag steht. Die erste Zahl benennt die Zeile, die zweite Zahl die Spalte: Der Eintrag ![]() einer Matrix
einer Matrix ![]() steht in der
steht in der ![]() -ten Zeile und
-ten Zeile und ![]() -ten Spalte.
-ten Spalte.
In unserem Beispiel oben ist also ![]() , denn in der zweiten Zeile von
, denn in der zweiten Zeile von ![]() steht in der ersten Spalte die Zahl
steht in der ersten Spalte die Zahl ![]() .
.
Beachte, dass es in der Regel nur möglich ist, zu sagen, welche Zahl in der Matrix an der Stelle ![]() steht, aber nicht umgekehrt, an welcher Stelle
steht, aber nicht umgekehrt, an welcher Stelle ![]() eine vorgegebene Zahl steht. Denn die Zahlen in der Matrix können mehrfach vorkommen. In unserem Beispiel steht die Zahl
eine vorgegebene Zahl steht. Denn die Zahlen in der Matrix können mehrfach vorkommen. In unserem Beispiel steht die Zahl ![]() sowohl in der ersten Zeile der ersten Spalte als auch in der dritten Zeile der zweiten Spalte. Daher ist
sowohl in der ersten Zeile der ersten Spalte als auch in der dritten Zeile der zweiten Spalte. Daher ist ![]() .
.
Typen von Matrizen
Es gibt viele verschiedene Typen von Matrizen. Im Allgemeinen ist die Anzahl der Zeilen einer Matrix ungleich der Anzahl der Spalten.
- Matrizen, die nur eine Zeile oder Spalte haben, können als Vektoren aufgefasst werden. Dabei ist eine
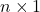 -Matrix ein Spaltenvektor, eine
-Matrix ein Spaltenvektor, eine  -Matrix heißt Zeilenvektor.
-Matrix heißt Zeilenvektor. - Matrizen mit der gleichen Anzahl von Zeilen und Spalten nennt man quadratische Matrizen. Zum Beispiel sind
 -Matrizen und
-Matrizen und 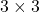 -Matrizen quadratisch, aber
-Matrizen quadratisch, aber  -Matrizen und
-Matrizen und  -Matrizen sind nicht quadratisch.
-Matrizen sind nicht quadratisch. - Eine Matrix heißt symmetrisch, wenn ihre Zeilen und Spalten übereinstimmen, d. h., wenn die erste Zeile gleich der ersten Spalte ist, die zweite Zeile gleich der zweiten Spalte usw. Hier ist ein Beispiel und ein Gegenbeispiel:
Die Matrix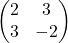 ist symmetrisch, die Matrix
ist symmetrisch, die Matrix  ist nicht symmetrisch.
ist nicht symmetrisch. - Eine symmetrische Matrix heißt Diagonalmatrix, wenn alle Einträge mit zwei verschiedenen Indexen null sind. Die Einträge, bei denen beide Zahlen des Doppelindex übereinstimmen, heißen Diagonaleinträge. Bei einer Diagonalmatrix sind also höchstens die Diagonaleinträge von null verschieden. Aber auch Diagonaleinträge dürfen null sein. Hier sind zwei Beispiele und Gegenbeispiele:
Die Matrizen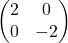 und
und 
sind Diagonalmatrizen. Die Matrizen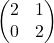 und
und  sind keine Diagonalmatrizen.
sind keine Diagonalmatrizen. - Ein spezieller Typ von Diagonalmatrizen sind die Einheitsmatrizen. Eine Matrix heißt Einheitsmatrix, wenn für alle Einträge der Form
 gilt:
gilt:  , und für alle anderen Einträge (also alle Einträge
, und für alle anderen Einträge (also alle Einträge  mit
mit  ) gilt:
) gilt: 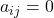 . Mit anderen Worten: Eine Einheitsmatrix ist eine Diagonalmatrix, bei der auf der Diagonalen überall
. Mit anderen Worten: Eine Einheitsmatrix ist eine Diagonalmatrix, bei der auf der Diagonalen überall  steht. Zu jeder natürlichen Zahl
steht. Zu jeder natürlichen Zahl 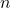 gibt es genau eine Einheitsmatrix der Ordnung
gibt es genau eine Einheitsmatrix der Ordnung  . Im Folgenden siehst du als Beispiel die Einheitsmatrizen der Ordnung
. Im Folgenden siehst du als Beispiel die Einheitsmatrizen der Ordnung  ,
,  und
und 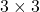 :
:
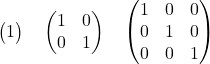
Rechnen mit Matrizen
Wir wollen nun die wichtigsten Rechenregeln beim Rechnen mit Matrizen betrachten.
Addition und Skalar-Multiplikation von Matrizen
Zwei Matrizen der gleichen Ordnung kann man addieren. Dabei werden alle Einträge einzeln addiert und das Ergebnis ist wieder eine Matrix der gleichen Ordnung. Diese Addition von Matrizen wird durch ein Beispiel einfach erklärt:
Wir addieren die Matrizen
![]() und
und ![]()
Die Summe ist die Matrix
![]()
Eine Matrix ![]() kann auch mit einem Skalar, also einer reellen Zahl, multipliziert werden. Diese Skalar-Multiplikation geht genauso wie bei Vektoren: Wir multiplizieren jeden einzelnen Eintrag mit dem Skalar.
kann auch mit einem Skalar, also einer reellen Zahl, multipliziert werden. Diese Skalar-Multiplikation geht genauso wie bei Vektoren: Wir multiplizieren jeden einzelnen Eintrag mit dem Skalar.
Wir schauen uns das an einem Beispiel an und multiplizieren die Matrix ![]() mit dem Skalar
mit dem Skalar ![]() :
:
![]()
Durch diese Addition und Skalar-Multiplikation können wir mit Matrizen der gleichen Ordnung rechnen.
Multiplikation von Vektoren mit Matrizen
Eine ![]() -Matrix
-Matrix ![]() kann man mit einem Vektor
kann man mit einem Vektor ![]() der Länge
der Länge ![]() multiplizieren. Das Produkt
multiplizieren. Das Produkt ![]() ist wieder ein Vektor der Länge
ist wieder ein Vektor der Länge ![]() . Die
. Die ![]() -te Komponente des Vektors
-te Komponente des Vektors ![]() erhältst du, indem du das Skalarprodukt der
erhältst du, indem du das Skalarprodukt der ![]() -ten Zeile von
-ten Zeile von ![]() mit dem Vektor
mit dem Vektor ![]() berechnest. Wir verdeutlichen das an einem Beispiel und multiplizieren die Matrix
berechnest. Wir verdeutlichen das an einem Beispiel und multiplizieren die Matrix
 mit dem Vektor
mit dem Vektor 
Das Produkt ist der Vektor

Multiplikation von Matrizen
Eine weitere Rechenoperation mit Matrizen ist die Matrix-Multiplikation. Zwei Matrizen ![]() und
und ![]() beliebiger Ordnung können nicht miteinander multipliziert werden. Um das Produkt
beliebiger Ordnung können nicht miteinander multipliziert werden. Um das Produkt ![]() berechnen zu können, muss die Anzahl der Spalten von
berechnen zu können, muss die Anzahl der Spalten von ![]() mit der Anzahl der Zeilen von
mit der Anzahl der Zeilen von ![]() übereinstimmen. Die Matrix
übereinstimmen. Die Matrix ![]() hat dann genauso viele Zeilen wie
hat dann genauso viele Zeilen wie ![]() und genauso viele Spalten wie
und genauso viele Spalten wie ![]() . Mit anderen Worten: Eine
. Mit anderen Worten: Eine ![]() -Matrix
-Matrix ![]() kann mit einer
kann mit einer ![]() -Matrix multipliziert werden. Als Produkt
-Matrix multipliziert werden. Als Produkt ![]() ergibt sich eine
ergibt sich eine ![]() -Matrix.
-Matrix.
Die Einträge von ![]() werden folgendermaßen berechnet: An der Stelle
werden folgendermaßen berechnet: An der Stelle ![]() steht das Skalarprodukt der
steht das Skalarprodukt der ![]() -ten Zeile von
-ten Zeile von ![]() mit der
mit der ![]() -ten Spalte von
-ten Spalte von ![]() :
:
![]()
Wir zeigen das an einem konkreten Beispiel und berechnen das Produkt der Matrizen
![]()
und

![]() ist eine
ist eine ![]() -Matrix und
-Matrix und ![]() eine
eine ![]() -Matrix. Wir können die Matrizen multiplizieren, weil
-Matrix. Wir können die Matrizen multiplizieren, weil ![]() genauso viele Spalten hat, wie
genauso viele Spalten hat, wie ![]() Zeilen hat. Das Produkt
Zeilen hat. Das Produkt ![]() ist die folgende
ist die folgende ![]() -Matrix:
-Matrix:

Die Matrizen ![]() und
und ![]() aus unserem Beispiel können wir auch umgekehrt multiplizieren, denn die Anzahl der Spalten von
aus unserem Beispiel können wir auch umgekehrt multiplizieren, denn die Anzahl der Spalten von ![]() ist gleich der Anzahl der Zeilen von
ist gleich der Anzahl der Zeilen von ![]() . Das Produkt
. Das Produkt ![]() ist dann eine
ist dann eine ![]() -Matrix:
-Matrix:
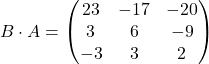
An diesen Beispielen erkennst du deutlich, dass die Matrix-Multiplikation nicht kommutativ ist: Die Matrizen ![]() und
und ![]() sind nicht gleich. In unserem Beispiel haben
sind nicht gleich. In unserem Beispiel haben ![]() und
und ![]() nicht einmal die gleiche Ordnung.
nicht einmal die gleiche Ordnung.
Quadratische Matrizen der gleichen Ordnung können immer in beiden Richtungen miteinander multipliziert werden. Aber auch hier ist die Matrix-Multiplikation nicht kommutativ. Wir zeigen wieder ein Beispiel und multiplizieren die Matrizen
![]() und
und ![]()
Die beiden Produkte sind:
![]()
und
![]()
Matrizen transponieren
Eine weitere wichtige Rechenoperation mit Matrizen ist die Transposition. Die Transponierte ![]() einer Matrix
einer Matrix ![]() erhältst du, indem du die Zeilen und Spalten der Matrix vertauschst: Aus der ersten Zeile wird die erste Spalte (und umgekehrt), aus der zweiten Zeile wird die zweite Spalte usw. Die Transponierte einer
erhältst du, indem du die Zeilen und Spalten der Matrix vertauschst: Aus der ersten Zeile wird die erste Spalte (und umgekehrt), aus der zweiten Zeile wird die zweite Spalte usw. Die Transponierte einer ![]() -Matrix ist dann eine
-Matrix ist dann eine ![]() -Matrix.
-Matrix.
Wir machen das an einem Beispiel deutlich: Die Transponierte der Matrix
![]() ist die Matrix
ist die Matrix 
Im Allgemeinen kannst du die Einträge der transponierten Matrix bestimmen, indem du bei den Einträgen der Matrix ![]() die beiden Zahlen des Doppelindex vertauscht. Steht in der Matrix
die beiden Zahlen des Doppelindex vertauscht. Steht in der Matrix ![]() in der
in der ![]() -ten Zeile und
-ten Zeile und ![]() -ten Spalte der Eintrag
-ten Spalte der Eintrag ![]() , ist es bei der transponierten Matrix umgekehrt: An der Stelle
, ist es bei der transponierten Matrix umgekehrt: An der Stelle ![]() steht der Eintrag
steht der Eintrag ![]() aus der Matrix
aus der Matrix ![]() , d. h.
, d. h. ![]() .
.
Bei symmetrischen Matrizen kann die Transposition auch benutzt werden, um zu überprüfen, ob die Matrix symmetrisch ist: Eine Matrix ist genau dann symmetrisch, wenn gilt: ![]() .
.
Die Determinante
Die Determinante ![]() einer Matrix
einer Matrix ![]() ist eine Zahl
ist eine Zahl ![]() . Sie existiert nur für quadratische Matrizen. Für die Determinante einer Matrix sind die Bezeichnungen
. Sie existiert nur für quadratische Matrizen. Für die Determinante einer Matrix sind die Bezeichnungen ![]() ,
, ![]() oder
oder ![]() geläufig.
geläufig.
Wir zeigen hier die Berechnung der Determinante für ![]() -Matrizen und für
-Matrizen und für ![]() -Matrizen. Die Berechnung der Determinante einer
-Matrizen. Die Berechnung der Determinante einer ![]() -Matrix geht ähnlich, ist aber etwas umfangreicher.
-Matrix geht ähnlich, ist aber etwas umfangreicher.
Die Formel für die Determinante einer ![]() -Matrix lautet:
-Matrix lautet:
![]()
Du multipliziert also die Einträge auf der Diagonalen und subtrahierst davon das Produkt der beiden anderen Einträge. Wir berechnen ein konkretes Beispiel:
![]()
Die Formel für die Determinante einer ![]() -Matrix lautet:
-Matrix lautet:
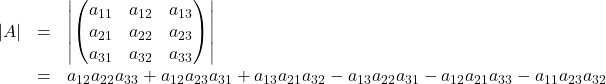
Du multiplizierst die Einträge auf den drei Hauptdiagonalen (die von links oben nach rechts unten verlaufen) und subtrahierst davon die Produkte der drei Nebendiagonalen.
Wir berechnen wieder ein konkretes Beispiel:

Anwendungen von Matrizen
Matrizen haben in der Mathematik viele verschiedene Anwendungen. Wir erklären im folgenden die Anwendung von Matrizen
- zur Flächen- und Volumenberechnung,
- zum Testen von Vektoren auf lineare Unabhängigkeit,
- zur Formulierung linearer Gleichungssysteme und
- bei Berechnungen mit Übergangsmatrizen.
Berechnung von Flächeninhalten und Volumina
Die Determinante einer Matrix wird verwendet, um Flächeninhalte oder Volumina zu berechnen. Für Flächeninhalte wird eine ![]() -Matrix, für Volumina eine
-Matrix, für Volumina eine ![]() -Matrix genutzt.
-Matrix genutzt.
Flächeninhalt von Dreiecken und Parallelogrammen
Die Determinante ist ein gutes Werkzeug, um den Flächeninhalt von Parallelogrammen oder Dreiecken in der Ebene zu berechnen. Du benötigst nur die Koordinaten der drei Eckpunkte ![]() ,
, ![]() und
und ![]() des Dreiecks.
des Dreiecks.
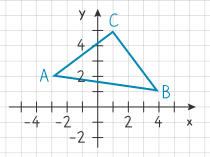
In unserem Beispiel ist ![]() ,
, ![]() und
und ![]() . Aus den Koordinaten berechnest du die Verbindungsvektoren
. Aus den Koordinaten berechnest du die Verbindungsvektoren
![]()
und
![]()
Nun schreibst du diese beiden Vektoren als Spalten in eine Matrix ![]() . Dabei soll die Reihenfolge der Vektoren so sein, dass die Drehung vom ersten zum zweiten Vektor gegen den Uhrzeigersinn erfolgt. Mit anderen Worten: Die Vektoren sollen eine rechtshändig orientierte Basis bilden. In unserem Beispiel ist
. Dabei soll die Reihenfolge der Vektoren so sein, dass die Drehung vom ersten zum zweiten Vektor gegen den Uhrzeigersinn erfolgt. Mit anderen Worten: Die Vektoren sollen eine rechtshändig orientierte Basis bilden. In unserem Beispiel ist ![]() die richtige Reihenfolge. Wir erhalten also die Matrix:
die richtige Reihenfolge. Wir erhalten also die Matrix:
![]()
Der Flächeninhalt des Dreiecks ![]() ist:
ist:

Was passiert, wenn die Vektoren ![]() ,
, ![]() nicht rechtshändig orientiert sind? Das können wir einfach erklären, indem wir in der Matrix oben die beiden Spalten vertauschen:
nicht rechtshändig orientiert sind? Das können wir einfach erklären, indem wir in der Matrix oben die beiden Spalten vertauschen:
![]()
Wenn wir jetzt in die Formel für den Flächeninhalt einsetzen, erhalten wir:
![]()
Die falsche Reihenfolge der Spaltenvektoren ändert das Vorzeichen der Determinante. Wenn du über die Reihenfolge der Vektoren nicht nachdenken willst, kannst du in der Formel für den Flächeninhalt des Dreiecks immer den Betrag der Determinante nehmen. Dann erhältst du automatisch das richtige Vorzeichen:
![]()
Analog zum Flächeninhalt von Dreiecken berechnest du auch den Flächeninhalt des von zwei Vektoren ![]() und
und ![]() aufgespannten Parallelogramms
aufgespannten Parallelogramms ![]() . In unserem Beispiel mit
. In unserem Beispiel mit ![]() und
und ![]() ist das von
ist das von ![]() und
und ![]() aufgespannte Parallelogramm genau die Verdoppelung des Dreiecks
aufgespannte Parallelogramm genau die Verdoppelung des Dreiecks ![]() . Daher ist der Flächeninhalt des Parallelogramms doppelt so groß wie der des Dreiecks: Du schreibst die Vektoren
. Daher ist der Flächeninhalt des Parallelogramms doppelt so groß wie der des Dreiecks: Du schreibst die Vektoren ![]() und
und ![]() als Spalten in eine Matrix
als Spalten in eine Matrix ![]() und berechnest den Betrag der Determinante dieser Matrix:
und berechnest den Betrag der Determinante dieser Matrix:
![]()
Volumen von Parallelotopen
Drei linear unabhängige Vektoren ![]() ,
, ![]() und
und ![]() im dreidimensionalen Raum spannen ein Parallelotop
im dreidimensionalen Raum spannen ein Parallelotop ![]() auf. Ein Parallelotop ist die dreidimensionale Verallgemeinerung eines Parallelogramms. Das Volumen dieses Parallelotops berechnest du ganz analog zum Flächeninhalt eines Parallelogramms in der zweidimensionalen Ebene: Du schreibst die drei Vektoren als Spalten in eine Matrix
auf. Ein Parallelotop ist die dreidimensionale Verallgemeinerung eines Parallelogramms. Das Volumen dieses Parallelotops berechnest du ganz analog zum Flächeninhalt eines Parallelogramms in der zweidimensionalen Ebene: Du schreibst die drei Vektoren als Spalten in eine Matrix ![]() . Das Volumen des Parallelotops
. Das Volumen des Parallelotops ![]() ist der Betrag der Determinante von
ist der Betrag der Determinante von ![]() :
:
![]()
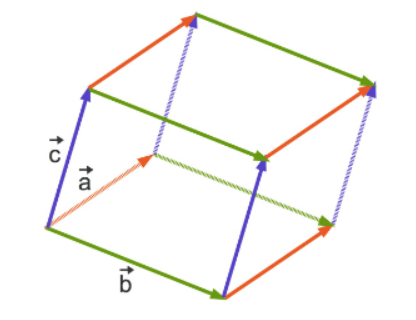
Wir berechnen als Beispiel das Volumen ![]() des von den Vektoren
des von den Vektoren 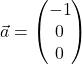 und
und  und
und  aufgespannten Parallelotops
aufgespannten Parallelotops ![]() :
:

Lineare Unabhängigkeit von Vektoren
Vektoren im dreidimensionalen Raum kannst du mithilfe der Determinante auf lineare Unabhängigkeit testen. Die Vektoren ![]() ,
, ![]() und
und ![]() sind genau dann linear unabhängig, wenn die Determinante der Matrix
sind genau dann linear unabhängig, wenn die Determinante der Matrix ![]() mit diesen Vektoren als Spalten ungleich null ist:
mit diesen Vektoren als Spalten ungleich null ist:
![]() linear unabhängig
linear unabhängig ![]()
Wir erläutern das an einem Beispiel und betrachten die Vektoren
 ,
,  und
und 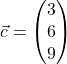
Auf den ersten Blick ist nicht zu erkennen, ob die Vektoren linear abhängig oder linear unabhängig sind. Wir schreiben die Vektoren als Spalten in die Matrix ![]() :
:
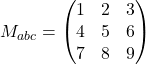
Nun berechnen wir die Determinante dieser Matrix:

Die Vektoren ![]() ,
, ![]() und
und ![]() sind also linear abhängig.
sind also linear abhängig.
Lineare Gleichungssysteme mit Matrizen lösen
Die Informationen eines linearen Gleichungssystems können in Form einer quadratischen Matrix und eines Vektors notiert werden. Das Rechenverfahren zum Lösen linearer Gleichungssysteme kann dann auf die Matrix und den Vektor der rechten Seite angewendet werden. Wir zeigen an einem Beispiel, wie du aus einem linearen Gleichungssystem die Matrix und den Vektor der rechten Seite gewinnst.
Als Beispiel verwenden wir das lineare Gleichungssystem:

Die Koeffizientenmatrix ![]() dieses linearen Gleichungssystems wird aus den Koeffizienten der Variablen in den einzelnen Gleichungen gebildet. Wir schreiben die Koeffizienten der ersten Gleichung in die erste Zeile. Dabei steht der Koeffizient von
dieses linearen Gleichungssystems wird aus den Koeffizienten der Variablen in den einzelnen Gleichungen gebildet. Wir schreiben die Koeffizienten der ersten Gleichung in die erste Zeile. Dabei steht der Koeffizient von ![]() in der ersten Spalte, der Koeffizient von
in der ersten Spalte, der Koeffizient von ![]() in der zweiten Spalte usw. Vor der Variablen
in der zweiten Spalte usw. Vor der Variablen ![]() steht kein Koeffizient, dort ergänzen wir
steht kein Koeffizient, dort ergänzen wir ![]() als Koeffizienten.
als Koeffizienten.
![]()
In die zweite Zeile schreiben wir die Koeffizienten der zweiten Gleichung usw. In der dritten Zeile müssen wir beachten, dass die Variable ![]() nicht vorkommt. Wir ergänzen daher den Koeffizienten
nicht vorkommt. Wir ergänzen daher den Koeffizienten ![]() .
.
So erhalten wir die Koeffizientenmatrix des linearen Gleichungssystems:

Die Zahlen auf der rechten Seite des linearen Gleichungssystems schreiben wir in einen Vektor ![]() :
:

Die Variablen ![]() ,
, ![]() und
und ![]() schreiben wir ebenfalls in einen Vektor:
schreiben wir ebenfalls in einen Vektor:
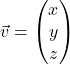
Mithilfe der Multiplikation von Matrizen und Vektoren können wir das lineare Gleichungssystem in der Form ![]() schreiben. Mit der Matrix
schreiben. Mit der Matrix ![]() und den Vektoren
und den Vektoren ![]() und
und ![]() sieht das so aus:
sieht das so aus:

Um ein lineares Gleichungssystem zu lösen, kannst du Additions- und Subtraktionsverfahren direkt auf eine erweiterte Koeffizientenmatrix anwenden: Du ergänzt die Matrix ![]() um den Vektor der rechten Seite. Die erweiterte Koeffizientenmatrix
um den Vektor der rechten Seite. Die erweiterte Koeffizientenmatrix ![]() sieht in unserem Beispiel so aus:
sieht in unserem Beispiel so aus:

Indem du mit der erweiterten Koeffizientenmatrix rechnest, ersparst du dir, in jeder Umformung alle Variablen mitzuschreiben. Auf diese Weise lässt sich das Lösen linearer Gleichungssysteme mit dem gaußschen Eliminationsverfahren durch die Matrizenrechnung sehr effizient organisieren.
Berechnungen mit Übergangsmatrizen
Wir zeigen an einem Beispiel, wie eine Matrix aus einer Sachaufgabe abgeleitet wird und die Matrizenrechnung hilft, die Aufgabe zu lösen:
Gegeben sind drei Stromanbieter mit Namen ![]() ,
, ![]() und
und ![]() . Die Unternehmen analysieren die Kundenbewegungen im Jahresdurchschnitt: Unternehmen
. Die Unternehmen analysieren die Kundenbewegungen im Jahresdurchschnitt: Unternehmen ![]() verliert jährlich im Durchschnitt
verliert jährlich im Durchschnitt ![]() seiner Kunden an Unternehmen
seiner Kunden an Unternehmen ![]() und
und ![]() seiner Unternehmen an das Unternehmen
seiner Unternehmen an das Unternehmen ![]() , die restlichen
, die restlichen ![]() sind Bestandskunden. Der Stromanbieter
sind Bestandskunden. Der Stromanbieter ![]() verliert nur
verliert nur ![]() seiner Kunden an
seiner Kunden an ![]() , aber keine an
, aber keine an ![]() . Und
. Und ![]() verliert
verliert ![]() seiner Kunden an
seiner Kunden an ![]() und
und ![]() seiner Kunden an
seiner Kunden an ![]() . Zum Zeitpunkt
. Zum Zeitpunkt ![]() betragen die Marktanteile der Unternehmen
betragen die Marktanteile der Unternehmen ![]() für Unternehmen
für Unternehmen ![]() und
und ![]() für Unternehmen
für Unternehmen ![]() . Da es zu diesem Zeitpunkt nur drei Unternehmen am Markt gibt, besteht der Marktanteil des Unternehmens
. Da es zu diesem Zeitpunkt nur drei Unternehmen am Markt gibt, besteht der Marktanteil des Unternehmens ![]() aus den verbleibenden
aus den verbleibenden ![]() .
.
Um die wirtschaftliche Entwicklung der Unternehmen beurteilen zu können, berechnen wir die Marktanteile der Unternehmen nach einem Jahr. Die Prozentsätze der Kundenbewegungen aus der Aufgabenstellung formen wir in Dezimalbrüche um. Die Kundenbewegungen zwischen den verschiedenen Anbietern sind in dem folgenden Übergangsdiagramm oder Flussdiagramm dargestellt:

Aus dem Diagramm bilden wir die Übergangsmatrix. Der Eintrag ![]() der Übergangsmatrix gibt den Anteil der Kunden an, die vom Stromanbieter der Nummer
der Übergangsmatrix gibt den Anteil der Kunden an, die vom Stromanbieter der Nummer ![]() zum Anbieter mit der Nummer
zum Anbieter mit der Nummer ![]() wechseln. Wir ordnen dem Anbieter
wechseln. Wir ordnen dem Anbieter ![]() die Nummer
die Nummer ![]() zu, dem Anbieter
zu, dem Anbieter ![]() die Nummer
die Nummer ![]() und dem Anbieter
und dem Anbieter ![]() die Nummer
die Nummer ![]() . Aus dem Diagramm erhalten wir die folgende Übergangsmatrix
. Aus dem Diagramm erhalten wir die folgende Übergangsmatrix ![]() :
:

Bei einer Übergangsmatrix ist die Summer der Einträge jeder Spalte ![]() .
.
Aus der Übergangsmatrix und den Marktanteilen der Unternehmen zum Zeitpunkt ![]() können wir die Marktanteile nach einem Jahr oder nach mehreren Jahren berechnen. Dazu schreiben wir die Marktanteile im Jahr
können wir die Marktanteile nach einem Jahr oder nach mehreren Jahren berechnen. Dazu schreiben wir die Marktanteile im Jahr ![]() in einen Vektor
in einen Vektor ![]() :
:

Die Verteilung der Marktanteile nach einem Jahr berechnen wir, indem wir die Übergangsmatrix ![]() mit dem Vektor
mit dem Vektor ![]() multiplizieren. Dies ergibt den Vektor
multiplizieren. Dies ergibt den Vektor ![]() der Marktanteile nach einem Jahr:
der Marktanteile nach einem Jahr:

Der große Gewinn der Matrixrechnung ist, dass wir direkt die Marktanteile nach zwei, drei oder vier Jahren berechnen können. Wenn wir voraussetzen, dass die jährlichen Durchschnitte der Kundenbewegungen immer gleich bleiben, multiplizieren wir den Anteile-Vektor ![]() mit der Übergangsmatrix
mit der Übergangsmatrix ![]() und erhalten den Vektor
und erhalten den Vektor ![]() der Marktanteile nach zwei Jahren:
der Marktanteile nach zwei Jahren:
![]()
Häufig gestellte Fragen zum Thema Matrizen


 ,
,
 ist eine Diagonalmatrix, die Matrix
ist eine Diagonalmatrix, die Matrix  ist keine Diagonalmatrix.
ist keine Diagonalmatrix.