Lineare Ungleichungen – Mathe
Erfahre, wie lineare Ungleichungen in Mathe funktionieren! Sie bestehen aus zwei Ausdrücken, verbunden durch Ungleichheitszeichen. Lerne, wie man sie löst und dabei die Inversionsregel beachtet. Dies und vieles mehr findest Du im folgenden Text!
Inhaltsverzeichnis zum Thema Lineare Ungleichungen
Lineare Ungleichung – Definition
Ungleichungen bestehen aus zwei Termen, zwischen denen eines der folgenden Zeichen steht: ![]() ,
, ![]() ,
, ![]() oder
oder ![]() . Eine Seite der Ungleichung ist größer als die andere: Die Seiten sind ungleich. Hat die Ungleichung die Form
. Eine Seite der Ungleichung ist größer als die andere: Die Seiten sind ungleich. Hat die Ungleichung die Form ![]() (
(![]() ) oder lässt sich durch Äquivalenzumformungen in diese Form bringen, dann sprechen wir von einer linearen Ungleichung mit einer Variablen.
) oder lässt sich durch Äquivalenzumformungen in diese Form bringen, dann sprechen wir von einer linearen Ungleichung mit einer Variablen.
Bedeutung der Zeichen:
| Zeichen | Bezeichnung | Bedeutung |
|---|---|---|
| Kleiner-als-Zeichen | Die linke Seite ist echt kleiner als die rechte Seite. | |
| Größer-als-Zeichen | Die linke Seite ist echt größer als die rechte Seite. | |
| Kleiner-gleich-Zeichen | Die linke Seite ist kleiner oder gleich der rechten Seite. | |
| Größer-gleich-Zeichen | Die linke Seite ist größer oder gleich der rechten Seite. |
Lineare Ungleichungen lösen
Ungleichungen können genauso wie normale Gleichungen gelöst werden. Auf beiden Seiten kann addiert, subtrahiert, multipliziert und dividiert werden, bis die gesuchte Variable allein steht. Allerdings gibt es eine wichtige zusätzliche Regel, die beim Lösen von Ungleichungen beachtet werden muss, die sogenannte Inversion.
Inversion
Das Ungleichheitszeichen dreht sich bei der Multiplikation oder Division mit einer negativen Zahl um. Das bedeutet: Aus ![]() wird
wird ![]() und aus
und aus ![]() wird
wird ![]() . Analog wird
. Analog wird ![]() zu
zu ![]() .
.
Betrachten wir dazu das folgende Beispiel:
![]()
Dividieren wir beide Seiten durch ![]() und lassen das Ungleichheitszeichen stehen, dann erhalten wir eine falsche Aussage:
und lassen das Ungleichheitszeichen stehen, dann erhalten wir eine falsche Aussage:
![]()
![]()
Um aus der falschen Aussage eine wahre Aussage zu machen, muss das Relationszeichen umgedreht werden:
![]()

Quelle sofatutor.com
Das Gleiche gilt für die Multiplikation mit negativen Zahlen.
Ansonsten gehen wir beim Lösen einer linearen Ungleichung genauso vor wie beim Lösen einer linearen Gleichung. Am einfachsten ist es zunächst, beide Seiten der Ungleichung, so weit es geht, zu vereinfachen. Im Anschluss kann die Ungleichung in zwei Schritten so umgeformt werden, dass die gesuchte Variable allein steht.
- Bringe alle Terme, in denen die Variable vorkommt, auf die eine und alle Terme, die die Variable nicht enthalten, auf die andere Seite der Ungleichung.
- Teile durch den Faktor vor der Variablen.
Beachtet werden muss zudem das richtige Aufschreiben der Lösungsmenge. Im Gegensatz zur Gleichung besitzt eine lineare Ungleichung nicht nur eine einzige Lösung, sondern eine Lösungsmenge in Form eines Intervalls. Besteht die Lösungsmenge beispielsweise aus allen Zahlen, die kleiner als ![]() sind, dann schreiben wir:
sind, dann schreiben wir:
![]()
Gelesen wird dieser Ausdruck als: ![]() ist die Menge aller
ist die Menge aller ![]() , für die gilt:
, für die gilt: ![]() ist kleiner als
ist kleiner als ![]() .
.
Eine alternative Schreibweise ist:
![]()
Bei dieser Schreibweise muss besonders beachtet werden, ob wir eine offene oder eine geschlossene eckige Klammer schreiben. Da die Ungleichung für alle ![]() kleiner als
kleiner als ![]() gilt, geht die Lösungsmenge von minus unendlich (
gilt, geht die Lösungsmenge von minus unendlich (![]() ) bis
) bis ![]() . Die linke Klammer ist offen, da es sich bei
. Die linke Klammer ist offen, da es sich bei ![]() nicht um eine wirkliche Zahl handelt und sie somit nicht Teil der Lösungsmenge sein kann. Die rechte Klammer ist ebenfalls offen, da das Ergebnis kleiner als
nicht um eine wirkliche Zahl handelt und sie somit nicht Teil der Lösungsmenge sein kann. Die rechte Klammer ist ebenfalls offen, da das Ergebnis kleiner als ![]() ist und die
ist und die ![]() somit nicht mehr zur Lösungsmenge gehört. Wäre die Lösungsmenge kleiner gleich
somit nicht mehr zur Lösungsmenge gehört. Wäre die Lösungsmenge kleiner gleich ![]() , wäre diese Klammer geschlossen.
, wäre diese Klammer geschlossen.
Lineare Ungleichungen – Aufgaben
Lineare Gleichungen und Ungleichungen können gelöst werden, indem sie so umgeformt werden, dass die gesuchte Variable allein auf einer Seite steht. Um alle Zahlen auf eine Seite zu bringen, können Zahlen auf beiden Seiten addiert, subtrahiert, multipliziert und dividiert werden.
Betrachten wir zunächst die folgende Ungleichung:
![]()
Wir wollen, dass das ![]() allein steht. Dafür muss das
allein steht. Dafür muss das ![]() auf die andere Seite gebracht werden. Dies erreichen wir, indem wir auf beiden Seiten
auf die andere Seite gebracht werden. Dies erreichen wir, indem wir auf beiden Seiten ![]() addieren.
addieren.
![]()
Die Variable ![]() ist also kleiner als
ist also kleiner als ![]() . Wir können dies auch als Lösungsmenge
. Wir können dies auch als Lösungsmenge ![]() schreiben:
schreiben:
![]()
oder
![]()
Betrachten wir eine zweite Aufgabe:
![]()
Zunächst bringen wir die beiden ![]() auf eine Seite und die beiden Zahlen ohne Variable auf die andere Seite der Ungleichung.
auf eine Seite und die beiden Zahlen ohne Variable auf die andere Seite der Ungleichung.
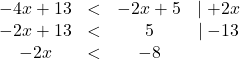 Damit das
Damit das ![]() allein steht, müssen wir im nächsten Schritt durch (
allein steht, müssen wir im nächsten Schritt durch (![]() ) dividieren. Dabei kehrt sich das Ungleichheitszeichen um.
) dividieren. Dabei kehrt sich das Ungleichheitszeichen um. ![]()
![]()
oder
![]()
Die Lösungsmenge umfasst alle Zahlen, die kleiner als ![]() sind.
sind.
Lineare Ungleichungen – Anwendung
Schauen wir uns nun an, wie wir eine lineare Ungleichung aus einer Textaufgabe aufstellen und lösen.
Aufgabe
Die Summe dreier aufeinanderfolgender Zahlen ist kleiner als ![]() .
.
Lineare Ungleichung aufstellen
Bei den drei aufeinanderfolgenden Zahlen handelt es sich um Variablen. Zunächst können wir die erste Zahl als Variable ![]() schreiben. Da es sich um aufeinanderfolgende Zahlen handelt, ist die zweite Zahl um eins und die dritte Zahl um zwei größer als die erste. Wir können sie also als
schreiben. Da es sich um aufeinanderfolgende Zahlen handelt, ist die zweite Zahl um eins und die dritte Zahl um zwei größer als die erste. Wir können sie also als ![]() und
und ![]() schreiben.
schreiben.
Zahl ![]() :
: ![]()
Zahl ![]() :
: ![]()
Zahl ![]() :
: ![]()
In der Aufgabe steht zudem, dass es sich um die Summe der drei Zahlen handelt. Wir addieren sie also.
![]()
Die Summe dieser drei Zahlen soll kleiner als ![]() sein. Das bedeutet, auf der anderen Seite der Ungleichung schreiben wir die
sein. Das bedeutet, auf der anderen Seite der Ungleichung schreiben wir die ![]() und zwischen beiden Termen steht ein
und zwischen beiden Termen steht ein ![]() .
.
![]()
Lineare Ungleichung lösen
Zunächst können wir die Klammern weglassen und alles addieren.

Damit das ![]() allein steht, ziehen wir nun die
allein steht, ziehen wir nun die ![]() auf beiden Seiten ab und teilen im Anschluss beide Seiten durch
auf beiden Seiten ab und teilen im Anschluss beide Seiten durch ![]() . Somit erhalten wir die Lösung:
. Somit erhalten wir die Lösung:
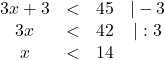
Das bedeutet, die kleinste der drei aufeinanderfolgenden Zahlen muss kleiner als ![]() sein. Wir können das durch das Einsetzen verschiedener Zahlen testen.
sein. Wir können das durch das Einsetzen verschiedener Zahlen testen.
![]()

Es handelt sich um eine wahre Aussage.
![]()
![]()
Es handelt sich um eine falsche Aussage.
Lineare Ungleichung mit zwei Variablen – grafisch lösen
Lineare Ungleichungen mit zwei Variablen besitzen die Form ![]() (
(![]() ) oder lassen sich durch Äquivalenzumformung in diese Form umwandeln. Die Lösungsmenge linearer Ungleichungen mit zwei Variablen ist eine Menge geordneter Zahlenpaare.
) oder lassen sich durch Äquivalenzumformung in diese Form umwandeln. Die Lösungsmenge linearer Ungleichungen mit zwei Variablen ist eine Menge geordneter Zahlenpaare.
Lineare Ungleichungen mit zwei Variablen lassen sich grafisch lösen. Dafür wird die Ungleichung zunächst so umgewandelt, dass das ![]() allein auf der linken Seite steht. Im Anschluss wird das Ungleichheitszeichen durch ein Gleichheitszeichen ausgetauscht, um die Funktionsgleichung zeichnen zu können. Die Lösungsmenge lässt sich dann je nach Ungleichheitszeichen folgendermaßen ablesen:
allein auf der linken Seite steht. Im Anschluss wird das Ungleichheitszeichen durch ein Gleichheitszeichen ausgetauscht, um die Funktionsgleichung zeichnen zu können. Die Lösungsmenge lässt sich dann je nach Ungleichheitszeichen folgendermaßen ablesen:
 Die Lösungsmenge ist der Bereich unterhalb des Funktionsgraphen.
Die Lösungsmenge ist der Bereich unterhalb des Funktionsgraphen. Die Lösungsmenge ist der Bereich oberhalb des Funktionsgraphen.
Die Lösungsmenge ist der Bereich oberhalb des Funktionsgraphen. Die Lösungsmenge umfasst den Bereich unterhalb des Funktionsgraphen und alle Punkte, die auf dem Funktionsgraphen liegen.
Die Lösungsmenge umfasst den Bereich unterhalb des Funktionsgraphen und alle Punkte, die auf dem Funktionsgraphen liegen. Die Lösungsmenge umfasst den Bereich oberhalb des Funktionsgraphen und alle Punkte, die auf dem Funktionsgraphen liegen.
Die Lösungsmenge umfasst den Bereich oberhalb des Funktionsgraphen und alle Punkte, die auf dem Funktionsgraphen liegen.
Betrachten wir die folgende Ungleichung:
![]()
Zunächst stellen wir die Gleichung so um, dass das ![]() auf der linken Seite allein steht:
auf der linken Seite allein steht:
![]()
Um die Ungleichung zu lösen, ersetzen wir das Ungleichheitszeichen durch ein Gleichheitszeichen und können die Gerade ![]() nun in ein Koordinatensystem einzeichnen.
nun in ein Koordinatensystem einzeichnen.

Da in der Ungleichung ein ![]() steht, gehören alle Punkte oberhalb der Geraden und auf der Geraden zur Lösungsmenge. Alle Punkte unterhalb der Geraden erfüllen die Ungleichung nicht.
steht, gehören alle Punkte oberhalb der Geraden und auf der Geraden zur Lösungsmenge. Alle Punkte unterhalb der Geraden erfüllen die Ungleichung nicht.
Betrachten wir ein weiteres Beispiel:
![]()
Auch diese Ungleichung formen wir zunächst so um, dass das ![]() auf der linken Seite allein steht.
auf der linken Seite allein steht.
![]()
Im Anschluss können wir zum Einzeichnen das Ungleichheitszeichen durch ein Gleichheitszeichen ersetzen und die Gerade ![]() einzeichnen.
einzeichnen.
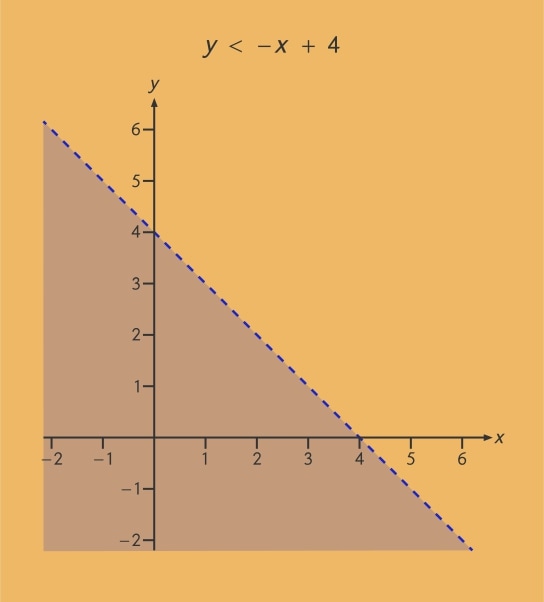
Da es sich hier um eine Ungleichung mit dem Kleiner-als-Zeichen handelt, zeichnen wir die Gerade gestrichelt ein, um deutlich zu machen, dass die Punkte auf der Geraden nicht mehr zur Lösungsmenge gehören. Lediglich die Punkte unterhalb der Geraden sind Lösungen der Ungleichung.
Spezialfälle von linearen Ungleichungen
Für die Lösungsmenge linearer Ungleichungen gibt es zwei Spezialfälle. So kann es vorkommen, dass:
- eine lineare Ungleichung unabhängig vom eingesetzten Wert immer falsch ist:
 .
. - eine lineare Ungleichung unabhängig vom eingesetzten Wert immer richtig ist:
 .
.
Beispiele:
Die Ungleichung ![]() ist immer falsch, da auf beiden Seiten
ist immer falsch, da auf beiden Seiten ![]() steht. Fällt dies durch Subtraktion weg, bleibt
steht. Fällt dies durch Subtraktion weg, bleibt ![]() stehen. Diese Aussage ist falsch und es gibt keinen Wert für
stehen. Diese Aussage ist falsch und es gibt keinen Wert für ![]() , bei dem die Ungleichung eine wahre Aussage liefert. Für diese Ungleichung gilt:
, bei dem die Ungleichung eine wahre Aussage liefert. Für diese Ungleichung gilt:
![]()
Im Gegensatz dazu ist die Ungleichung ![]() immer wahr. Auch hier kürzt sich der Term
immer wahr. Auch hier kürzt sich der Term ![]() durch Subtraktion und stehen bleibt
durch Subtraktion und stehen bleibt ![]() . Das ist eine wahre Aussage, egal welchen Wert wir für
. Das ist eine wahre Aussage, egal welchen Wert wir für ![]() einsetzen. Für diese Ungleichung gilt:
einsetzen. Für diese Ungleichung gilt:
![]()
Weitere Arten von Ungleichungen
Als weitere wichtige Arten der Ungleichungen existieren neben den linearen Ungleichungen noch die Bruchungleichungen und die quadratischen Ungleichungen. Bei Bruchungleichungen handelt es sich nicht einfach nur um lineare Ungleichungen mit Brüchen, sondern um Ungleichungen, die aus mindestens einem Bruchterm bestehen. Bruchterme sind Brüche, in denen eine Variable im Nenner steht.
Bruchungleichung Beispiel: ![]()
Im Gegensatz zu linearen Ungleichungen kommt das ![]() in quadratischen Ungleichungen immer mit der Potenz
in quadratischen Ungleichungen immer mit der Potenz ![]() vor, also als
vor, also als ![]() .
.
Quadratische Ungleichung Beispiel: ![]()
Häufig gestellte Fragen zum Thema Lineare Ungleichungen









