Brüche multiplizieren – Definition, Erklärung und Beispiele

Erfahre, wie Brüche Anteile beschreiben und wie man sie miteinander multipliziert. Entdecke die Regeln für die Zahlenkombination und das Kürzen vor der Multiplikation. Möchtest du wissen, wie Du Brüche über Kreuz multiplizieren kannst?

Inhaltsverzeichnis zum Thema Multiplikation von Brüchen

Teste dein Wissen

Wie multipliziert man Brüche miteinander?

Frage 1 von 5

Wann darf man über Kreuz multiplizieren?

Frage 2 von 5

Wie rechnet man Brüche mal?

Frage 3 von 5

Wie multipliziert man Brüche mit ungleichen Nennern?

Frage 4 von 5

Wie multipliziert man mehrere Brüche miteinander?

Frage 5 von 5

Brüche multiplizieren im Überblick

  • Brüche beschreiben Anteile und bestehen immer aus einem Zähler, dem Bruchstrich und einem Nenner.
  • Brüche werden miteinander multipliziert, indem man Zähler mal Zähler und Nenner mal Nenner rechnet.
  • Brüche können vor der Multiplikation gekürzt werden, um die Rechnung zu vereinfachen.
Brüche multiplizieren: Lernvideo

Quelle sofatutor.com

Brüche multiplizieren – Erklärung

Brüche beschreiben Anteile. Sie bestehen aus zwei Zahlen, die durch den Bruchstrich getrennt sind. Die obere Zahl wird Zähler und die untere Zahl Nenner genannt. Wie man Brüche multipliziert, wird im Folgenden einfach erklärt.
Wenn wir von der Multiplikation von Brüchen sprechen, dann ist die Rede von einer Multiplikation, bei der mindestens ein Faktor ein Bruch ist. Es können auch beide Faktoren Brüche sein.
Um zwei Brüche miteinander zu multiplizieren, rechnest du Zähler mal Zähler und Nenner mal Nenner. Das Ergebnis ist ebenfalls ein Bruch.

Brüche multiplizieren

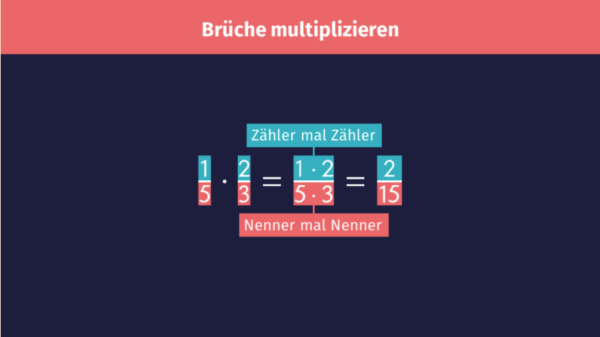
Das bedeutet, du multiplizierst den Zähler des ersten Bruchs mit dem Zähler des zweiten Bruchs. Das Produkt steht im Ergebnis als Zähler über dem Bruchstrich. Dann multiplizierst du den Nenner des ersten Bruchs mit dem Nenner des zweiten Bruchs. Das Produkt steht im Ergebnis als Nenner unter dem Bruchstrich.
Dabei spielt es keine Rolle, ob du gemeine oder unechte Brüche multiplizierst, die Vorgehensweise ist gleich. Auch bei der Multiplikation mehrerer Brüche gehst du genauso vor. Dabei steht im Zähler das Produkt aus allen Zählern und im Nenner das Produkt aus allen Nennern.

Beispiel:

\dfrac{1}{2} \cdot \dfrac{3}{4} = \dfrac{1 \cdot 3}{2 \cdot 4} = \dfrac{3}{8}

Du multiplizierst den Zähler des ersten Bruchs, die 1, mit dem Zähler des zweiten Bruchs, der 3. Das ergibt die 3 im Zähler des Ergebnisses. Außerdem multiplizierst du den Nenner des ersten Bruchs, die 2, mit dem Nenner des zweiten Bruchs, der 4. Dabei erhältst du die 8, die im Nenner des Ergebnisses steht.
Das Ergebnis der Multiplikation ist:
\dfrac{3}{8}

Brüche multiplizieren – Brüche vor der Multiplikation kürzen

Manche Brüche enthalten große Zahlen. Da das bei einer Multiplikation zu sehr großen Zahlen im Ergebnis führen kann, ist es sinnvoll, vorher zu schauen, ob sich Brüche kürzen lassen. Das kann das Rechnen deutlich vereinfachen.
Um Brüche kürzen zu können, müssen Zähler und Nenner einen gemeinsamen Teiler besitzen. Ist das der Fall, kann gekürzt werden, indem beide Zahlen durch diesen Teiler dividiert werden.

Beispiel:
\dfrac{12}{18} = \dfrac{12 : 6}{18 : 6} = \dfrac{2}{3}

Sowohl die 12 als auch die 18 sind durch 6 teilbar. Wir können den Bruch mit 6 kürzen und erhalten \frac{2}{3}. Mit diesem Bruch kann deutlich leichter weitergerechnet werden.

Beispiel: Kürzen vor der Multiplikation
\dfrac{12}{18} \cdot \dfrac{1}{3} = \dfrac{12 : 6}{18 : 6} \cdot \dfrac{1}{3} = \dfrac{2}{3} \cdot \dfrac{1}{3} = \dfrac{2}{9}

Eine Besonderheit bei der Multiplikation von Brüchen gibt es: Manchmal ist es notwendig, Brüche über Kreuz zu kürzen. Damit ist gemeint, dass der Zähler des einen Faktors mit dem Nenner des anderen Faktors gekürzt wird.

Im folgenden Beispiel kann die 3 aus dem Nenner des ersten Bruchs mit der 3 aus dem Zähler des zweiten Bruchs gekürzt werden.

\dfrac{2}{3} \cdot \dfrac{3}{5} = \dfrac{2}{\not{3}} \cdot \dfrac{\not{3}}{5} = \dfrac{2}{1} \cdot \dfrac{1}{5} = \dfrac{2}{5}

Das funktioniert, da du beide Brüche auf einen Bruchstrich schreiben kannst, bei dem Zähler und Nenner ein Produkt sind, aus dem gekürzt werden kann.

\dfrac{2}{3} \cdot \dfrac{3}{5} = \dfrac{2 \cdot 3}{3 \cdot 5} = \dfrac{2 \cdot \not{3}}{\not{3} \cdot 5} = \dfrac{2}{5}

Brüche multiplizieren – weitere Beispiele

Wir betrachten Beispiele für Produkte, bei denen ein oder mehrere Faktoren Brüche sind. Dabei schreiben wir die Faktoren, wenn nötig, zunächst als Bruch um. Im Anschluss wird wie oben beschrieben Zähler mal Zähler und Nenner mal Nenner gerechnet. Die folgende Tabelle fasst die verschiedenen Fälle zusammen.

Beispiel Rechnung Hinweis
mehrere Brüche miteinander multiplizieren \dfrac{1}{2} \cdot \dfrac{3}{4} \cdot \dfrac{2}{3} = \dfrac{1 \cdot 3 \cdot 2}{2 \cdot 4 \cdot 3} = \dfrac{6}{24} = \dfrac{1}{4} Alle Zähler werden miteinander multipliziert und alle Nenner werden miteinander multipliziert.
eine natürliche Zahl mit einem Bruch multiplizieren 5 \cdot \dfrac{2}{11} = \dfrac{5}{1} \cdot \dfrac{2}{11} = \dfrac{5 \cdot 2}{1 \cdot 11} = \dfrac{10}{11} Die ganze Zahl muss zunächst als Bruch geschrieben werden.
gemischte Brüche mit einem Bruch multiplizieren 2\dfrac{2}{5} \cdot \dfrac{2}{3} = \dfrac{12}{5} \cdot \dfrac{2}{3} = \frac{24}{15} Der gemischte Bruch muss zunächst als unechter Bruch geschrieben werden.
Brüche mit Variablen multiplizieren \dfrac{2}{3}x \cdot \dfrac{1}{2}y = \dfrac{2\,x \cdot 1\,y}{3 \cdot 2} = \dfrac{2\,xy}{6} = \dfrac{1\,xy}{3} Die Variable wird in den Zähler des Bruchs multipliziert.

Zusammenfassung – Multiplikationsregeln von Brüchen

  • Ist einer der Faktoren kein Bruch, muss dieser als Bruch geschrieben werden.
  • Alle Zähler werden miteinander multipliziert und ergeben den Zähler des Produkts.
  • Alle Nenner werden miteinander multipliziert und ergeben den Nenner des Produkts.

Kehrwert von Brüchen multiplizieren

Auch bei der Division von Brüchen spielt die Multiplikation eine wichtige Rolle. Um zwei Brüche zu dividieren, muss der Kehrwert des zweiten Bruchs mit dem ersten Bruch multipliziert werden. Mehr dazu erfährst du im entsprechenden Text.

Brüche über Kreuz multiplizieren

Bei Brüchen in Gleichungen wird das Verfahren des kreuzweisen Multiplizierens verwendet. Das Ziel ist es, die Gleichung ohne Brüche zu schreiben. Dafür wird der Nenner auf der einen Seite mit dem Zähler der anderen Seite multipliziert und andersherum.

Beispiel:
\begin{array}{cccl} \dfrac{x}{2} & = & \dfrac{4}{8} & \vert \cdot 2 \cdot 8 \\ x \cdot 8 & = & 4 \cdot 2 & \\ 8x & = & 8 & \vert : 8 \\ x & = & 1 \end{array}

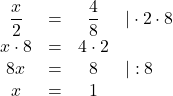
Achtung!
Steht im Zähler oder Nenner der Brüche eine Summe oder Differenz, muss diese in Klammern gesetzt werden.

Textaufgabe zum Thema Brüche multiplizieren

Betrachten wir die folgende Textaufgabe, um das Wissen über die Multiplikation von Brüchen anzuwenden.

Aufgabe:
Marie will für den Geburtstag ihrer Freundin einen Kuchen backen. Da ihre Kuchenform kleiner ist als die im Rezept angegebene, will sie nur \frac{2}{3} der im Rezept angegebenen Zutaten verwenden.
Wie viel Backpulver muss sie verwenden, wenn die im Rezept angegebene Menge \frac{1}{4} Esslöffel ist?

Lösung:
Da Marie \frac{2}{3} der Mengenangabe aus dem Rezept verwenden will, rechnen wir diesen Bruch mal die im Rezept angegebene Menge \frac{1}{4} und erhalten:

\dfrac{2}{3} \cdot \dfrac{1}{4} = \dfrac{2 \cdot 1}{3 \cdot 4} = \dfrac{2}{12} = \dfrac{1}{6}

Antwortsatz:
Marie muss nur \frac{1}{6} Esslöffel Backpulver verwenden.

Häufig gestellte Fragen zum Thema Brüche multiplizieren

Zwei Brüche werden miteinander multipliziert, indem man Zähler mal Zähler und Nenner mal Nenner rechnet. Als Ergebnis erhält man ebenfalls einen Bruch.

Um Brüche zu multiplizieren, wird der Zähler des ersten Bruchs mal den Zähler des zweiten Bruchs gerechnet. Das Produkt (also das Ergebnis der Malaufgabe) schreiben wir in den Zähler des Ergebnisses. Im Anschluss rechnen wir den Nenner des ersten Bruchs mal den Nenner des zweiten Bruchs. Das Produkt schreiben wir in den Nenner des Ergebnisses.

Auch wenn die Nenner der Brüche ungleich sind, wird Zähler mal Zähler und Nenner mal Nenner gerechnet. Für die Multiplikation von Brüchen müssen diese nicht gleichnamig sein.

Beim  Multiplizieren über Kreuz wird der Nenner des einen Bruchs mit dem Zähler des anderen Bruchs und umgekehrt multipliziert.

Die Überkreuz-Multiplikation wird bei der Lösung von Bruchgleichungen angewandt. Achte darauf, wenn nötig Klammern zu setzen.

Wenn ein Bruch vervielfacht, also mit einer ganzen Zahl multipliziert werden soll, muss die ganze Zahl zunächst als Bruch geschrieben werden. Im Anschluss wird Zähler mal Zähler und Nenner mal Nenner gerechnet.

Alle Zähler werden miteinander multipliziert und alle Nenner werden miteinander multipliziert. Die Vorgehensweise ist die gleiche wie bei zwei Brüchen, nur dass es mehrere Faktoren gibt.

Die Variablen werden in den Zähler geschrieben und im Anschluss können die Brüche normal multipliziert werden, also Zähler mal Zähler und Nenner mal Nenner.

Leave A Comment

Alle Artikel aus dem Fach Mathematik