pq-Formel – Erklärung und Beispiele
Die pq-Formel berechnet Lösungen quadratischer Gleichungen. Erfahre, wie sie angewendet wird, um Nullstellen zu finden. Entdecke die Herleitung der Formel und wie die Diskriminante die Anzahl der Lösungen bestimmt. Interessiert? Dies und vieles mehr erwartet dich im folgenden Text!
Inhaltsverzeichnis zum Thema pq-Formel
Wie willst du heute lernen?
pq-Formel einfach erklärt
Die ![]() -Formel wird verwendet, um quadratische Gleichungen der Form
-Formel wird verwendet, um quadratische Gleichungen der Form
![]()
zu lösen.
Dabei ist ![]() ist die unbekannte Variable, die berechnet werden soll. Vor dem
ist die unbekannte Variable, die berechnet werden soll. Vor dem ![]() steht eine
steht eine ![]() als Koeffizient,
als Koeffizient, ![]() ist der Koeffizient vor dem
ist der Koeffizient vor dem ![]() und
und ![]() die Konstante. Eine quadratische Gleichung ist eine Gleichung, in der der höchste Exponent (Hochzahl) der Variablen
die Konstante. Eine quadratische Gleichung ist eine Gleichung, in der der höchste Exponent (Hochzahl) der Variablen ![]() eine
eine ![]() ist.
ist.
Die ![]() -Formel lautet:
-Formel lautet:
![]()
In diese setzt du die Zahl, die vor dem einzelnen ![]() steht, für
steht, für ![]() ein und die Zahl, die allein steht, für
ein und die Zahl, die allein steht, für ![]() .
.
Da die rechte Seite der Gleichung null ist, berechnest du mit der ![]() -Formel die Nullstellen der quadratischen Funktion
-Formel die Nullstellen der quadratischen Funktion ![]() .
.
pq-Formel anwenden
Beispiel 1:
Die quadratische Gleichung liegt schon in der Normalform ![]() vor:
vor:
![]()
Daher können die Koeffizienten ![]() und
und ![]() direkt abgelesen werden.
direkt abgelesen werden.
Diese werden nun in die ![]() -Formel eingesetzt:
-Formel eingesetzt:
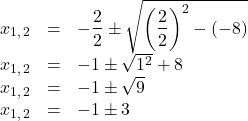
Hieraus können zwei Lösungen berechnet werden:
![]() und
und ![]()
Also ist die Lösungsmenge:
![]()
Beispiel 2:
Die quadratische Gleichung liegt noch nicht in der Normalform vor:
![]()
In diesem Beispiel steht vor dem ![]() der Koeffizient
der Koeffizient ![]() und auf der rechten Seite steht
und auf der rechten Seite steht ![]() .
.
Also muss die Gleichung zunächst in die Normalform ![]() gebracht werden, bevor mithilfe der
gebracht werden, bevor mithilfe der ![]() -Formel die Lösung der Gleichung ausgerechnet werden kann.
-Formel die Lösung der Gleichung ausgerechnet werden kann.
In diesem Beispiel bedeutet das:
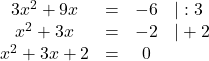
Jetzt können die Koeffizienten ![]() und
und ![]() in die pq-Formel eingesetzt werden:
in die pq-Formel eingesetzt werden:
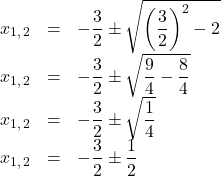
Somit gibt es zwei Lösungen. Für die erste Lösung rechnest du plus ![]() für die zweite minus
für die zweite minus ![]() :
:
![]() und
und ![]()
Damit ist die Lösungsmenge:
![]()
Nullstellen berechnen mithilfe der pq-Formel
Mit der ![]() -Formel berechnest du die Nullstellen einer Parabel, also einer quadratischen Funktion.
-Formel berechnest du die Nullstellen einer Parabel, also einer quadratischen Funktion.
An der Diskriminante ![]() , dem Term unterhalb der Wurzel in der
, dem Term unterhalb der Wurzel in der ![]() -Formel, kannst du eine Aussage darüber treffen, wie viele Nullstellen die Funktion
-Formel, kannst du eine Aussage darüber treffen, wie viele Nullstellen die Funktion ![]() besitzt.
besitzt.
Dabei gilt:
![]()
Für ![]() hat die Parabel zwei Nullstellen.
hat die Parabel zwei Nullstellen.
Für ![]() hat die Parabel genau eine Nullstelle, wegen
hat die Parabel genau eine Nullstelle, wegen ![]() .
.
Für ![]() gibt es keine Nullstellen, da die Wurzel aus einer negativen Zahl nicht definiert ist.
gibt es keine Nullstellen, da die Wurzel aus einer negativen Zahl nicht definiert ist.
Hier siehst du entsprechend Parabeln mit keiner Nullstelle in Blau, einer in Orange und zwei in Rot.
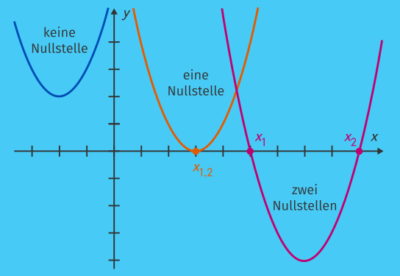
Herleitung der pq-Formel
Jetzt wurde erklärt, wofür die ![]() -Formel verwendet wird. Aber woher kommt diese Formel?
-Formel verwendet wird. Aber woher kommt diese Formel?
Dazu schauen wir uns eine quadratische Gleichung in Normalform an und bringen das ![]() mittels Subtraktion auf die rechte Seite:
mittels Subtraktion auf die rechte Seite:
![]()
Nun wollen wir eine quadratische Ergänzung durchführen.
Wir addieren zu beiden Seiten ![]() hinzu und schreiben
hinzu und schreiben ![]() um als
um als ![]() :
:
![]()
Durch Nutzung der ersten binomische Formel vereinfachen wir die linke Seite zu:
![]()
Als Letztes müssen wir nur noch die Wurzel auf beiden Seiten ziehen und die Gleichung nach ![]() umformen:
umformen:
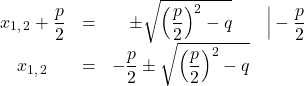
Hinweis: Beim Wurzelziehen muss darauf geachtet werden, dass es zwei Lösungen gibt, einmal plus und einmal minus. Das wird leicht sichtbar an der quadratischen Gleichung
. Die Lösung hierfür kann sowohl
als auch
sein, da
und
.
Die gleiche Herleitung für eine quadratische Gleichung in der allgemeinen Form ![]() liefert die sogenannte Mitternachtsformel (auch
liefert die sogenannte Mitternachtsformel (auch ![]() -Formel) zur Lösung quadratischer Gleichungen.
-Formel) zur Lösung quadratischer Gleichungen.
Die Mitternachtsformel lautet:
![]()
pq-Formel – Zusammenfassung
Um quadratische Gleichungen mithilfe der ![]() -Formel zu lösen, wird wie folgt vorgegangen:
-Formel zu lösen, wird wie folgt vorgegangen:
| Schritt | Beispiel |
|---|---|
| Gleichung in Normalform umschreiben:
|
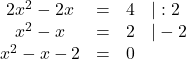 |
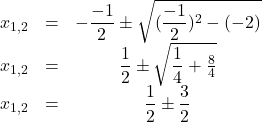 |
|
| Die Lösungen mit plus und minus berechnen | |
| Lösungsmenge aufschreiben |
Wenn die gestellte Aufgabe lediglich darin besteht, zu sagen, wie viele Lösungen die Gleichung bzw. wie viele Nullstellen die Funktion ![]() hat, reicht es, sich die Diskriminante
hat, reicht es, sich die Diskriminante ![]() anzuschauen. Für diese gilt:
anzuschauen. Für diese gilt:
| Diskriminante | Lösungen |
|---|---|
| zwei Lösungen | |
| eine Lösung | |
| keine Lösung |
Häufig gestellte Fragen zum Thema pq-Formel









Alle Artikel aus dem Fach Mathematik