Primzahlen einfach erklärt
Primzahlen sind natürliche Zahlen, die nur durch 1 und sich selbst teilbar sind. Erfahre, warum sie eine Schlüsselrolle bei mathematischen Prozessen spielen und wie du sie mithilfe von Teilbarkeitsregeln erkennst. Dies und vieles mehr findest du im folgenden Text.
Inhaltsverzeichnis zum Thema Primzahlen
Primzahlen – Erklärung
Primzahlen sind ganze, natürliche Zahlen, die nur durch sich selbst und durch ![]() teilbar sind. Sie besitzen also nur genau zwei Teiler.
teilbar sind. Sie besitzen also nur genau zwei Teiler.
Die Primzahlen von ![]() bis
bis ![]() sind in der folgenden Liste aufgezählt:
sind in der folgenden Liste aufgezählt:
![]()
Außer der ![]() sind alle Primzahlen ungerade. Das liegt daran, dass jede gerade Zahl größer als
sind alle Primzahlen ungerade. Das liegt daran, dass jede gerade Zahl größer als ![]() auch durch
auch durch ![]() teilbar ist und somit mindestens
teilbar ist und somit mindestens ![]() Teiler besitzt. Damit ist die
Teiler besitzt. Damit ist die ![]() die einzige gerade Primzahl.
die einzige gerade Primzahl.
Bei der ![]() und der
und der ![]() handelt es sich, wie du erkennen kannst, nicht um Primzahlen. Die
handelt es sich, wie du erkennen kannst, nicht um Primzahlen. Die ![]() ist zwar durch
ist zwar durch ![]() , jedoch nicht durch sich selbst teilbar. Da Primzahlen immer genau zwei Teiler besitzen müssen, ist auch die
, jedoch nicht durch sich selbst teilbar. Da Primzahlen immer genau zwei Teiler besitzen müssen, ist auch die ![]() keine Primzahl. Somit ist die
keine Primzahl. Somit ist die ![]() die erste Primzahl.
die erste Primzahl.
Kleinste und größte Primzahl
Es existiert keine größte Primzahl, da es unendlich viele Primzahlen gibt. Die kleinste Primzahl ist die erste Primzahl ![]() .
.
Negative Primzahlen
Es gibt keine negativen Primzahlen, da die Definition der Primzahlen besagt, dass es sich bei den Primzahlen um natürliche Zahlen handelt.
Primzahlzwillinge
Von Primzahlzwillingen spricht man, wenn zwei Primzahlen den Abstand ![]() zueinander haben. Es ist nicht bekannt, wie viele Primzahlzwillinge existieren. Die Primzahlzwillinge bis
zueinander haben. Es ist nicht bekannt, wie viele Primzahlzwillinge existieren. Die Primzahlzwillinge bis ![]() sind:
sind: ![]() und
und ![]() ,
, ![]() und
und ![]() ,
, ![]() und
und ![]() ,
, ![]() und
und ![]() ,
, ![]() und
und ![]() ,
, ![]() und
und ![]() ,
, ![]() und
und ![]() .
.
Primzahldrillinge
Von Primzahldrillingen spricht man, wenn drei Primzahlen jeweils den Abstand ![]() zueinander haben. Die einzigen existierenden Primzahldrillinge sind
zueinander haben. Die einzigen existierenden Primzahldrillinge sind ![]() ,
, ![]() und
und ![]() .
.
Primzahlen erkennen
Um Primzahlen zu bestimmen, gibt es zwei verschiedene Methoden, die im Folgenden genauer erklärt werden.
Primzahlen mithilfe der Teilbarkeitsregeln erkennen
Die Teilbarkeitsregeln sind nützlich, um Primzahlen zu erkennen. So kannst du herausfinden, ob eine Zahl noch weitere Teiler als ![]() und sich selbst besitzt. Schauen wir uns die Vorgehensweise am Beispiel der
und sich selbst besitzt. Schauen wir uns die Vorgehensweise am Beispiel der ![]() an:
an:
- Die
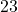 ist ungerade und aus diesem Grund nicht durch
ist ungerade und aus diesem Grund nicht durch 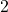 teilbar.
teilbar. - Andere Teiler müssten daher kleiner als die Hälfte von
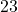 sein. Es kommen also nur die Zahlen
sein. Es kommen also nur die Zahlen 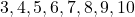 und
und  infrage.
infrage. - Da die
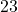 ungerade ist, ist sie sicher auch nicht durch die geraden Zahlen
ungerade ist, ist sie sicher auch nicht durch die geraden Zahlen 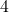 ,
, 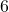 und
und 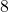 teilbar.
teilbar. - Ist die Quersumme einer Zahl durch
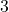 teilbar, dann ist auch die Zahl durch
teilbar, dann ist auch die Zahl durch 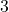 teilbar. Die Quersumme von
teilbar. Die Quersumme von 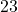 ist
ist 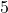 . Da
. Da 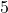 nicht durch
nicht durch 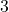 teilbar ist, ist auch die
teilbar ist, ist auch die 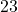 nicht durch
nicht durch 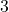 teilbar.
teilbar. - Durch
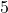 ist eine Zahl nur dann teilbar, wenn die letzte Ziffer eine
ist eine Zahl nur dann teilbar, wenn die letzte Ziffer eine 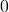 oder eine
oder eine 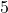 ist. Das ist bei der
ist. Das ist bei der 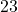 nicht der Fall.
nicht der Fall. - Durch
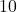 ist eine Zahl nur dann teilbar, wenn ihre letzte Ziffer eine
ist eine Zahl nur dann teilbar, wenn ihre letzte Ziffer eine 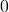 ist. Somit ist die
ist. Somit ist die 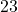 auch nicht durch
auch nicht durch 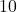 teilbar.
teilbar. - Bleibt nur noch die
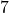 ,
, 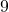 und die
und die  . Aber da die
. Aber da die 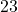 kein Teil der
kein Teil der 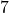 er-,
er-, 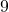 er- oder
er- oder  er-Reihe ist, ist sie auch nicht durch eine der drei Zahlen teilbar.
er-Reihe ist, ist sie auch nicht durch eine der drei Zahlen teilbar.
Die Teiler von ![]() sind also
sind also ![]() und
und ![]() . Die
. Die ![]() ist damit eine Primzahl.
ist damit eine Primzahl.

Quelle sofatutor.com
Sieb des Eratosthenes
Mit dem Sieb des Eratosthenes können aus einer endlichen Liste an Zahlen alle Primzahlen herausgesiebt werden. Es ist ein systematisches Verfahren, um alle Primzahlen einer bestimmten Zahlenmenge zu bestimmen.
Dafür werden zunächst alle natürlichen Zahlen beginnend bei der ![]() bis zur festgelegten größten Zahl aufgelistet. Die weitere Vorgehensweise ist dann wie folgt:
bis zur festgelegten größten Zahl aufgelistet. Die weitere Vorgehensweise ist dann wie folgt:
- Zunächst wählen wir die kleinste Zahl in der Liste, also die
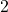 , aus und umkreisen diese. Alle Vielfachen der
, aus und umkreisen diese. Alle Vielfachen der 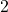 werden nun durchgestrichen, da es sich bei ihnen nicht um Primzahlen handelt.
werden nun durchgestrichen, da es sich bei ihnen nicht um Primzahlen handelt. - Nun suchen wir die nächstgrößere noch nicht durchgestrichene Zahl. Das ist in diesem Fall die
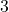 . Wir umkreisen diese Zahl ebenfalls. Alle Vielfachen der
. Wir umkreisen diese Zahl ebenfalls. Alle Vielfachen der 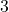 werden durchgestrichen.
werden durchgestrichen. - Diese Vorgehensweise wird so lange fortgeführt, bis alle Zahlen umkreist oder durchgestrichen sind.
- Bei allen umkreisten Zahlen handelt es sich um Primzahlen. Alle durchgestrichenen Zahlen sind keine Primzahlen.
Mit diesem Verfahren kann eine endliche Liste an Zahlen auf ihre Primzahlen reduziert werden. Eine Formel zur Berechnung aller Primzahlen einer bestimmten Menge ist nicht bekannt.
Primzahlen – Beispiele
In der Schule ist es nützlich, die Primzahlen bis ![]() auswendig zu können. Die folgende Tabelle zeigt die Primzahlen bis 100 in verschiedenen Abstufungen und kann dir beim Lernen helfen.
auswendig zu können. Die folgende Tabelle zeigt die Primzahlen bis 100 in verschiedenen Abstufungen und kann dir beim Lernen helfen.
| Zahlen | Anzahl | |
|---|---|---|
| Primzahlen bis |
||
| Primzahlen bis |
||
| Primzahlen bis |
||
| Primzahlen bis |
Primzahlen – Anwendung
Primzahlen spielen in verschiedenen mathematischen Prozessen eine Rolle. So sind Primzahlen besonders bei der Primfaktorzerlegung von Bedeutung. Aber auch bei der Bestimmung des größten gemeinsamen Teilers (![]() ) und des kleinsten gemeinsamen Vielfachen (
) und des kleinsten gemeinsamen Vielfachen (![]() ) ist es wichtig, dass du dich mit Primzahlen auskennst.
) ist es wichtig, dass du dich mit Primzahlen auskennst.
Häufig gestellte Fragen zum Thema Primzahlen

