Kongruenz Mathe – Definition, Erklärung und Beispiele
Lerne, wie Kongruenz in der Geometrie die Deckungsgleichheit von Figuren beschreibt. Entdecke die Bedeutung von Kongruenzabbildungen und die Unterschiede zwischen ähnlichen und kongruenten Figuren. Interessiert? Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Kongruenz
Kongruenz – Definition
Kongruenz ist in Mathe ein Begriff aus dem Bereich der Geometrie, der die Deckungsgleichheit zweier geometrischer Figuren bezeichnet. Deckungsgleich bedeutet, dass zwei Figuren in Größe und Form völlig übereinstimmen, also so übereinander gelegt werden können, dass sie sich vollständig überdecken. In diesem Fall sind alle Winkel und Seiten der Figuren gleich. Wir sagen: Die beiden Figuren sind kongruent zueinander.
Kongruente Figuren können durch Kongruenzabbildungen aufeinander abgebildet werden.
Kongruenzabbildungen – Bedeutung
Manchmal ist die Kongruenz zweier Figuren nicht auf den ersten Blick sichtbar. Woran das liegt, schauen wir uns gemeinsam an.
- Drehen wir eine Figur in eine neue Position, ändern sich weder die Form noch die Größe der Figur. Wird sie zurückgedreht, passt sie exakt wieder auf die Ausgangsfigur.
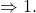 Figuren sind auch dann kongruent, wenn sie durch Drehen aufeinander abgebildet werden können.
Figuren sind auch dann kongruent, wenn sie durch Drehen aufeinander abgebildet werden können. - Die Form und Größe einer Figur ändert sich auch beim Verschieben nicht.
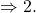 Figuren sind auch dann kongruent, wenn sie durch Verschiebung aufeinander abgebildet werden können.
Figuren sind auch dann kongruent, wenn sie durch Verschiebung aufeinander abgebildet werden können. - Beim Spiegeln einer Figur an einer Achse bleiben Längen und Winkel und damit die Form und Größe ebenfalls erhalten.
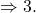 Figuren sind auch dann kongruent, wenn sie durch Spiegelung an einer Achse aufeinander abgebildet werden können.
Figuren sind auch dann kongruent, wenn sie durch Spiegelung an einer Achse aufeinander abgebildet werden können.
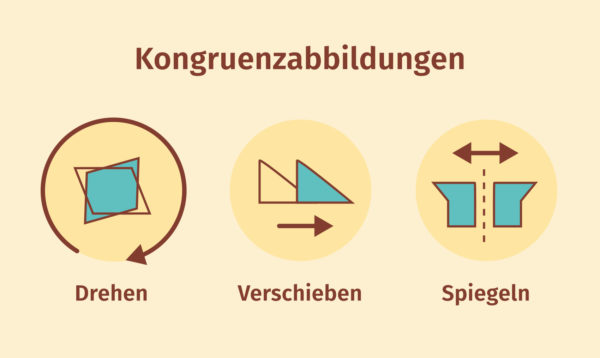
Drehen, Verschieben und Spiegeln werden als Kongruenzabbildungen bezeichnet. Kongruente Figuren können stets durch eine Kombination dieser drei Operationen aufeinander abgebildet werden.
Unterschied ähnlich und kongruent in Mathe
Zwei Figuren sind ähnlich, wenn sie zwar in ihrer Form, aber nicht unbedingt in ihrer Größe übereinstimmen. Bei kongruenten Figuren müssen die Form und die Größe übereinstimmen.
Ähnliche Figuren können neben den Kongruenzabbildungen auch durch eine Streckung auseinander hervorgehen. Dabei wird die Figur vergrößert oder verkleinert. Die Streckung ist keine Kongruenzabbildung.
Zusammenfassung – Kongruenz und Ähnlichkeit:
- Kongruente Figuren stimmen in allen Seiten und Winkeln überein. Sie können durch die drei Kongruenzabbildungen Drehen, Verschieben oder Spiegeln aufeinander abgebildet werden.
- Ähnliche Figuren stimmen in allen Winkeln überein. Neben den Kongruenzabbildungen ist hier auch eine Streckung zulässig, die die Figur bei gleichbleibenden Seitenverhältnissen vergrößert oder verkleinert.
Kongruenz – Beispiele
Betrachten wir die Figuren in der folgenden Grafik:
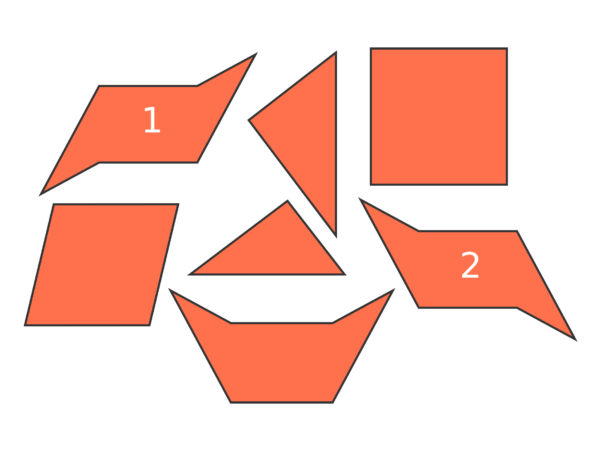
Welche der Figuren sind kongruent zueinander?
Betrachten wir zunächst die beiden Vierecke. Auf den ersten Blick scheinen die Seitenlängen und die Größe übereinzustimmen. Da die Winkel jedoch verschieden sind, können sie durch Verschiebung nicht genau aufeinander abgebildet werden. Sie sind also nicht kongruent zueinander.
Bei den Dreiecken stimmt zwar die Form überein, allerdings ist das obere Dreieck größer als das untere. Es handelt sich also um ähnliche, aber nicht um kongruente Dreiecke.
Die mit ![]() und
und ![]() beschrifteten Figuren besitzen sowohl die gleiche Form als auch die gleiche Größe. Wird eine der Figuren gespiegelt und verschoben, kann sie genau auf die andere abgebildet werden. Figur
beschrifteten Figuren besitzen sowohl die gleiche Form als auch die gleiche Größe. Wird eine der Figuren gespiegelt und verschoben, kann sie genau auf die andere abgebildet werden. Figur ![]() und
und ![]() sind demnach kongruent zueinander.
sind demnach kongruent zueinander.
Kongruenzsätze für Dreiecke – Definition
Mithilfe der Kongruenzsätze lassen sich kongruente Dreiecke erkennen. Die folgende Tabelle zeigt eine Übersicht über die Kongruenzsätze.
| Kongruenzsatz | Erklärung |
|---|---|
| SSS | Zwei Dreiecke stimmen in allen drei Seitenlängen überein. |
| SWS | Zwei Dreiecke stimmen in zwei Seiten und dem davon eingeschlossenen Winkel überein. |
| WSW | Zwei Dreiecke stimmen in einer Seite und den beiden anliegenden Winkeln überein. |
| SsW | Zwei Dreiecke stimmen in zwei Seiten und dem der längeren Seite gegenüberliegenden Winkel überein. |

In den Abkürzungen stehen die S für Seiten und die W für Winkel. Können wir einen der Kongruenzsätze nachweisen, sind die Dreiecke deckungsgleich. Da die Angaben, die einen der Kongruenzsätze erfüllen, ausreichen, um ein Dreieck, bis auf Kongruenzabbildungen, eindeutig zu beschreiben, kann ein Dreieck aus diesen Angaben eindeutig konstruiert werden.
Häufig gestellte Fragen zum Thema Kongruenz

