Winkelhalbierende – Definition, Eigenschaften und Konstruktion
Winkelhalbierende teilen Winkel in zwei gleich große Teile und finden sich in vielen geometrischen Figuren. Entdecke, wie man Winkelhalbierende konstruiert und ihre Rolle im Dreieck, Viereck und regelmäßigen Polygonen.
Inhaltsverzeichnis zum Thema Winkelhalbierende
Definition und Eigenschaften der Winkelhalbierenden
Ein Winkel hat feste Größen und liegt immer zwischen zwei sich schneidenden Strecken oder Halbgeraden. Der Winkelscheitel befindet sich im Schnittpunkt, die beiden geraden Linien bilden die Schenkel des Winkels.

Ein Winkel wird, wie der Name schon verrät, von seiner Winkelhalbierenden halbiert. Es entstehen zwei gleich große Winkel, die zusammen den ursprünglichen Winkel bilden.

Alle Punkte auf der Winkelhalbierenden haben den gleichen Abstand zu den beiden Schenkeln, da sie genau in der Mitte zwischen ihnen verläuft.
Konstruktion der Winkelhalbierenden
Für die Konstruktion der Winkelhalbierenden benötigst du einen Zirkel und ein Lineal. Bei der Konstruktion kannst du dich dann an die folgende Schrittfolge halten:
- Stich den Zirkel im Scheitelpunkt ein und zeichne einen Kreisbogen so, dass er beide Schenkel schneidet. Markiere diese Schnittpunkte.

- Die beiden Schnittpunkte dienen dir als Mittelpunkte für zwei weitere Kreise. Wähle den Radius der beiden Kreise gleich groß und so, dass die beiden Kreise sich schneiden.


- Zeichne die Winkelhalbierende, indem du eine Halbgerade vom Scheitelpunkt aus durch die Schnittpunkte der beiden Kreise ziehst. Diese Halbgerade ist die Winkelhalbierende.

In der folgenden Abbildung sind alle Schritte zur Konstruktion der Winkelhalbierenden zusammengefasst.

Winkelhalbierende in verschiedenen geometrischen Figuren
Die meisten geometrischen Figuren besitzen Ecken. Diese schließen Winkel ein, sodass es für jeden Winkel auch eine Winkelhalbierende gibt. Eine geometrische Figur besitzt also so viele Winkelhalbierende, wie sie auch Ecken beziehungsweise Winkel besitzt.
Es gibt beispielsweise keine Winkelhalbierenden im Kreis, da ein Kreis keine Ecken hat. Ein Dreieck hingegen hat entsprechend drei Winkelhalbierende.
Die Winkelhalbierenden einer geometrischen Figur können einen gemeinsamen Schnittpunkt aufweisen. Hat eine Figur einen solchen gemeinsamen Schnittpunkt aller Winkelhalbierenden, ist dieser der Mittelpunkt des Inkreises der geometrischen Figur. Der Inkreis berührt alle Seiten der Figur, sein Mittelpunkt ist also von allen Seiten gleich weit entfernt.
Schneiden sich alle Winkelhalbierenden einer Figur in einem Punkt, ist dieser Schnittpunkt Mittelpunkt des Inkreises.
Der Inkreis berührt alle Seiten der Figur. Da jede Winkelhalbierende so verläuft, dass sie zu zwei Seiten den gleichen Abstand hat, gilt für ihren Schnittpunkt, dass er von allen Seiten gleich weit entfernt ist.
Durch die Konstruktion der Winkelhalbierenden kannst du also auch den Inkreis konstruieren. Hier siehst du dies am Beispiel eines Dreiecks.
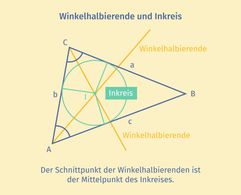
Winkelhalbierende im Dreieck
Die Winkelhalbierenden im Dreieck schneiden sich immer in einem Punkt innerhalb des Dreiecks. Jedes Dreieck besitzt also einen Inkreis.

Bei den verschiedenen Arten von Dreiecken gibt es Besonderheiten bezüglich der Winkelhalbierenden:
- Im gleichseitigen Dreieck stimmen die Winkelhalbierenden mit den Mittelsenkrechten überein.
- Im rechtwinkligen Dreieck halbiert die Winkelhalbierende des rechten Winkels auch den Winkel, der zwischen der Höhe und der Seitenhalbierenden der Hypotenuse eingeschlossen wird.
Hinweis: Da sich die Winkelhalbierenden eines Dreiecks immer in einem Punkt schneiden, ist es für die Konstruktion des Inkreismittelpunkts ausreichend, den Schnittpunkt anhand von zwei der drei Winkelhalbierenden zu konstruieren.
Winkelhalbierende im Viereck
Im Gegensatz zum Dreieck hat nicht jedes Viereck einen Inkreis, der alle Seiten der Figur berührt. Einen solchen Kreis gibt es nur dann, wenn alle Winkelhalbierenden sich in einem Punkt schneiden.
Die Winkelhalbierenden eines Drachenvierecks schneiden sich beispielsweise immer in einem Punkt. Daher hat jedes Drachenviereck einen Inkreis.
Die Winkelhalbierenden im Parallelogramm hingegen können aneinander vorbeiführen und besitzen dann keinen gemeinsamen Schnittpunkt. Ein Parallelogramm hat also im Allgemeinen keinen Inkreis.
Winkelhalbierende im regelmäßigen Polygon
Ein regelmäßiges Polygon (auch regelmäßiges Vieleck) ist ein Vieleck, dessen Seiten alle gleich lang und dessen Innenwinkel gleich groß sind.
Betrachtest du die Winkelhalbierenden in einem regelmäßigen Polygon, wird dir auffallen, dass diese sich immer in einem Punkt schneiden. Es gibt also einen Inkreis.
Beispielhaft kannst du dies an diesem regelmäßigen Fünfeck beobachten. Auch regelmäßige Acht- oder Zehnecke erfüllen diese Eigenschaft, ebenso wie jedes regelmäßige ![]() -Eck.
-Eck.

Häufig gestellte Fragen zum Thema Winkelhalbierende

