Trigonometrische Funktionen ableiten – Sinus-, Cosinus- und Tangensfunktion

Trigonometrische Funktionen abzuleiten bedeutet, die Ableitungen von Sinus, Cosinus und Tangens zu berechnen. Erfahre, wie sie mit Ableitungsregeln kombiniert werden können und welche Besonderheiten es gibt.

Inhaltsverzeichnis zum Thema Trigonometrische Funktionen ableiten

Trigonometrische Funktionen ableiten im Überblick

  • Die Ableitung der Sinusfunktion: f(x)=\sin (x) ist f^\prime(x)=\cos (x)

  • Die Ableitung der Cosinusfunktion: f(x)=\cos (x) ist f^\prime(x)=-\sin (x)

  • Die Ableitung der Tangensfunktion: f(x)=\tan (x) ist f^\prime(x) = \frac{1}{\cos ^{2}(x)}

  • Trigonometrische Funktionen können mit anderen Funktionen verknüpft und mithilfe der Ableitungsregeln abgeleitet werden.

Trigonometrische Funktionen ableiten: Lernvideo

Quelle sofatutor.com

Trigonometrische Funktionen

Als trigonometrische Funktionen werden die Winkelfunktionen bezeichnet. Primär geht es um

  • die Sinusfunktion,
  • die Cosinusfunktion und
  • die Tangensfunktion.

Wie andere Funktionen auch können sie abgeleitet werden.

Ableitung von Sinusfunktionen

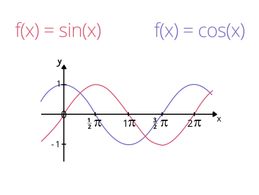
Betrachte zunächst die Funktion f(x)=\sin (x). Welche Punkte kannst du erkennen und was verraten diese über die zugehörige Ableitung?

Sinusfunktion

Die Sinusfunktion hat Hochpunkte bei \left( \frac{\pi}{2}+2 \pi \cdot k \vert 1 \right) und Tiefpunkte bei \left( -\frac{\pi}{2}+2 \pi \cdot k \vert -1 \right).

Die Ableitung muss an den Hoch- und Tiefpunkten der Funktion Nullstellen haben.
Am Funktionsgraph der Cosinusfunktion ist zu erkennen, dass diese genau an den Hoch- und Tiefpunkten der Sinusfunktion Nullstellen besitzt.
Wenn f(x)=\sin (x) ist, gilt also f^\prime(x)=\cos (x). Die Cosinusfunktion ist die Ableitung der Sinusfunktion.

Sinus- und Kosinusfunktion

Ableitung von Cosinusfunktionen

Dass die Cosinusfunktion die Ableitung der Sinusfunktion ist, weißt du nun. Aber was ist die Ableitung der Cosinusfunktion?

Hochpunkte der Kosinusfunktion

Die Cosinusfunktion besitzt ihre Hochpunkte bei (2 \pi \cdot k \vert 1).
Die Tiefpunkte sind bei (\pi \cdot k \vert -1) zu finden.

Tiefpunkte der Kosinusfunktion

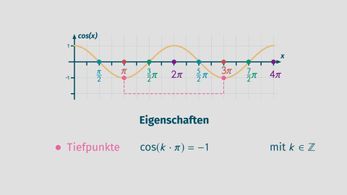
Genau an diesen Stellen besitzt der Funktionsgraph der Funktion f(x)=-\sin (x) Nullstellen.
Die Ableitung der Cosinusfunktion ist also die negative Sinusfunktion.
Für f(x) = \cos(x) gilt also:
f^\prime(x) = -\sin(x)

Vielleicht ist dir schon aufgefallen, dass Sinus- und Cosinusfunktion bezüglich der Ableitungen in Zusammenhang stehen. Mit der folgenden Abbildung kannst du dir die Ableitungen von Sinus- und Cosinusfunktion gut merken.

Ableitung von Sinus- und Kosinusfunktionen

Tangensfunktionen ableiten

Für die Ableitung der Tangensfunktion greifen wir auf die anderen trigonometrischen Funktionen sowie die Quotientenregel zurück.
Dafür wird die Tangensfunktion zunächst umgeschrieben.

f(x)= \tan (x)= \frac{\sin (x)}{\cos (x)}

Da du bereits weißt, wie Sinus und Cosinus abgeleitet werden, kannst du die Ableitung mithilfe der Quotientenregel berechnen.

f^\prime(x)=\frac{\cos (x) \cdot \cos (x)- \sin (x) \cdot (-\sin (x))}{\cos^{2}(x)}=\frac{\cos ^{2}(x)+\sin ^{2}(x)}{\cos ^{2}(x)}=\frac{1}{\cos ^{2}(x)}

Alternativ ergibt sich auch:

f^\prime(x)=\frac{\cos (x) \cdot \cos (x)- \sin (x) \cdot (-\sin (x))}{\cos^{2}(x)}=\frac{\cos ^{2}(x)+\sin ^{2}(x)}{\cos ^{2}(x)}=1+\frac{\sin ^{2}(x)}{\cos ^{2}(x)}=1+\tan ^{2}(x)

Ableitungsregeln trigonometrischer Funktionen

Nicht immer liegen dir die trigonometrischen Funktionen allein vor. Es kann vorkommen, dass sie mit anderen Funktionen verknüpft sind. Dann benötigst du die Ableitungsregeln.

Ableitung von Summen mit trigonometrischen Funktionen

Trigonometrische Funktionen können mit jeder anderen Funktion addiert werden. So kann es vorkommen, dass du die Ableitung einer Summe von trigonometrischen Funktionen und einer Exponentialfunktion bilden musst.

Betrachte die Funktion f(x)=\sin (x)+e^{x} und bilde ihre Ableitung.

Um die Ableitung der Summe zu bilden, betrachtest du die Ableitungen der beiden Summanden einzeln. Es gilt (\sin (x))^\prime=\cos (x) und (e^{x})^\prime=e^{x}.
Anschließend addierst du die beiden Ableitungen und erhältst die Ableitung der Funktion f(x):
f^\prime(x)=\cos (x)+e^{x}

Ableitung von trigonometrischen Funktionen mit der Kettenregel

Auch Verkettungen von trigonometrischen Funktionen untereinander oder mit anderen Funktionen sind möglich. Dann verwendest du die Kettenregel.

Die Funktion g(x)=\sin (x^{2}) ist eine Verkettung der Funktionen u(x)=\sin (x) und v(x)=x^{2}. Die Sinusfunktion wird hier als äußere und die quadratische Funktion als innere Funktion bezeichnet.
Um die Ableitung zu bilden, leitest du zunächst die innere und die äußere Funktion einzeln ab. Anschließend setzt du diese wieder wie folgt zusammen:
f^\prime(x)=u^\prime(v(x)) \cdot v^\prime(x)

u^\prime(x)= \cos (x)
v^\prime(x)= 2x

f^\prime(x)=\cos (x^{2}) \cdot 2x

Eine weitere Verkettung ist beispielsweise die Funktion h(x)=-\sin (\cos (x)). Die Ableitung dieser Funktion lautet:
h^\prime(x)=-\cos (\cos (x)) \cdot (-\sin (x))

Ableitung von trigonometrischen Funktionen mit der Produktregel

Trigonometrische Funktionen können miteinander multipliziert werden. Deshalb kann es nötig sein, dass du die Ableitung von Sinusfunktionen mithilfe der Produktregel berechnen musst.
Betrachte die Funktion f(x)=\sin (x) \cdot \sin (x).
Die Funktion besteht aus einer Multiplikation zweier Sinusfunktionen. Die Ableitung der Sinusfunktion ist die Cosinusfunktion. Mithilfe der Produktregel kannst du die Ableitung der ganzen Funktion bilden:

f^\prime(x)=\cos (x) \cdot \sin (x) + \sin (x) \cdot \cos(x)=2\cdot sin(x) \cdot cos(x)

Zusammenfassung der Ableitungen trigonometrischer Funktionen

Die folgende Tabelle fasst die wichtigsten Ableitungen trigonometrischer Funktionen zusammen.

Trigonometrische Funktion Ableitung
\sin (x) \cos (x)
\cos (x) -\sin (x)
-\sin (x) -\cos (x)
-\cos (x) \sin (x)
\tan (x) \frac{1}{\cos ^{2}(x)}
\cot (x) -\dfrac{1}{\sin^{2} (x)}

Häufig gestellte Fragen zum Thema Trigonometrische Funktionen ableiten

Die Sinusfunktion ergibt abgeleitet die Cosinusfunktion.

Die Cosinusfunktion ergibt abgeleitet die negative Sinusfunktion.

Die Tangensfunktion ist abgeleitet (\tan (x))^\prime=\frac{1}{\cos ^{2}(x)}=1+\tan ^{2}(x).

Die Bezeichnung \cot entspricht dem Cotangens, also dem Kehrwert des Tangens. Seine Ableitung ist -\dfrac{1}{\sin^{2}(x)}.

Beim Ableiten trigonometrischer Funktionen kannst du dir, genau wie bei jeder anderen Funktionsklasse, entweder den Funktionsgraphen anschauen und grafisch ableiten oder du betrachtest die Tangenten in konkreten Punkten, um auf die Ableitungsfunktion schließen zu können.

Summen trigonometrischer Funktionen werden mit der Summenregel abgeleitet. Du berechnest die Ableitung der einzelnen Summanden und addierst diese anschließend.

Sind trigonometrische Funktionen mit anderen Funktionen verkettet, leitest du diese mit der Kettenregel ab. Dafür berechnest du die Ableitung der äußeren Funktion u(x) und der inneren Funktion v(x) und setzt diese dann in folgende Formel ein: f^\prime(x)=u^\prime(v(x)) \cdot v^\prime(x).

Besteht eine Funktion aus dem Produkt mehrerer trigonometrischer Funktionen, kannst du die Produktregel anwenden. Die Ableitung einer Funktion der Form f(x)=u(x) \cdot v(x) ist dann f^\prime(x)=u^\prime(x) \cdot v(x)+u(x) \cdot v^\prime(x).

Die Quotientenregel kannst du bei trigonometrischen Funktionen genauso anwenden wie bei allen anderen Funktionen auch. Eine Funktion der Form f(x)=\frac{u(x)}{v(x)} leitest du mit der Formel \frac{u^\prime(x) \cdot v(x)-u(x) \cdot v^\prime(x)}{(v(x))^{2}} ab.

Ist eine trigonometrische Funktion mit einer Exponentialfunktion verknüpft, leitest du diese mit der entsprechenden Ableitungsregel ab. Dafür brauchst du die Ableitung der trigonometrischen Funktion und die der Exponentialfunktion.

Umkehrfunktionen trigonometrischer Funktionen haben ebenso entsprechende Ableitungen. Um diese zu finden, kannst du die Tangenten der Umkehrfunktion in verschiedenen Punkten betrachten, um auf die Ableitung schließen zu können.

Als Grundlage für die Ableitung trigonometrischer Funktionen betrachtest du die Tangenten in verschiedenen Punkten. Diese verraten dir, an welchen Stellen die Ableitungsfunktion Nullstellen haben muss. Die Hoch- und Tiefpunkte sind in diesem Fall besonders aussagekräftig.

In der Schule genügt es meist, wenn du die Ableitung der gängigen trigonometrischen Funktionen Sinus, Cosinus und Tangens kennst.

Für Klausuraufgaben mit trigonometrischen Funktionen solltest du wissen, wie die einzelnen trigonometrischen Funktionen abgeleitet werden, und Ableitungsregeln kennen.

Die Ableitungen trigonometrischer Funktionen wendest du in Aufgaben der Analysis an. Trigonometrische Funktionen können beispielsweise in Kurvendiskussionen vorkommen.

Trigonometrische Funktionen sind im Gegensatz zu vielen anderen Funktionen periodisch. Das bedeutet, dass sie innerhalb einer bestimmten Periode immer wieder die gleichen Funktionswerte annehmen. Dies gilt genauso für deren Ableitungen.

Leave A Comment

Alle Artikel aus dem Fach Mathematik