Was ist ein Vektor? – Grundlagen zu Vektoren
Lerne, was Vektoren sind und wie sie durch Länge und Richtung definiert werden. Entdecke, wie man Vektoren im Koordinatensystem darstellt, ihre Länge berechnet und sie addiert oder subtrahiert. Beeindruckende Beispiele und häufig gestellte Fragen warten auf dich!
Inhaltsverzeichnis zum Thema Vektoren
Vektor – Definition und Erklärung
Wird ein Punkt im Koordinatensystem verschoben, dann ändern sich der ![]() -Wert und der
-Wert und der ![]() -Wert des Punktes. Als Vektor wird die Verschiebung des Punktes bezeichnet. Vektoren werden als Pfeile im Koordinatensystem dargestellt. Sie sind definiert durch ihre Länge und ihre Richtung. Dargestellt wird also, in welche Richtung und wie weit ein Punkt verschoben wurde.
-Wert des Punktes. Als Vektor wird die Verschiebung des Punktes bezeichnet. Vektoren werden als Pfeile im Koordinatensystem dargestellt. Sie sind definiert durch ihre Länge und ihre Richtung. Dargestellt wird also, in welche Richtung und wie weit ein Punkt verschoben wurde.

Ist eine Größe durch ihre Länge und ihre Richtung definiert, dann sprechen wir von einem Vektor.
Vektoren – Schreibweise
Vektoren werden entweder als Kleinbuchstaben mit einem Pfeil darüber bezeichnet (![]() ,
, ![]() …) oder als Strecke zwischen Start- und Endpunkt mit einem Pfeil darüber (
…) oder als Strecke zwischen Start- und Endpunkt mit einem Pfeil darüber (![]() ,
, ![]() …).
…).
Im zweidimensionalen Koordinatensystem bestehen die Vektoren aus zwei Koordinaten, die wir übereinander schreiben.
![]()
Dabei ist ![]() die Verschiebung in Rightung der
die Verschiebung in Rightung der ![]() -Achse und
-Achse und ![]() die Verschiebung in Richtung der
die Verschiebung in Richtung der ![]() -Achse.
-Achse.
Vektor – Beispiel: ![]()
Vektoren im dreidimensionalen Raum besitzen zusätzlich noch eine dritte Koordinate für die Verschiebung in Richtung der ![]() -Achse.
-Achse.

Vektor eines Punktes im Koordinatensystem bilden
Jeder Punkt ![]() im Koordinatensystem lässt sich mit seinen Koordinaten als Vektor darstellen. Dabei ist
im Koordinatensystem lässt sich mit seinen Koordinaten als Vektor darstellen. Dabei ist ![]() die Verschiebung in
die Verschiebung in ![]() -Richtung und
-Richtung und ![]() die Verschiebung in
die Verschiebung in ![]() -Richtung vom Ursprung
-Richtung vom Ursprung ![]() aus. Die Vektorschreibweise lautet dann:
aus. Die Vektorschreibweise lautet dann:
![]()
Die Koordinaten des Vektors entsprechen also den Koordinaten des Punktes.
Für Vektoren im dreidimensionalen Raum gilt analog:

Da ein solcher Vektor den Ort beschreibt, an dem sich ein Punkt im Koordinatensystem befindet, wird er auch als Ortsvektor bezeichnet.
Beispiel:
Gegeben ist der Punkt ![]() . Der zugehörige Ortsvektor lautet:
. Der zugehörige Ortsvektor lautet:
![]()
Vektoren zwischen zwei Punkten berechnen
Wollen wir Vektoren zwischen zwei Punkten bestimmen, müssen wir die Koordinaten des Anfangspunktes von den Koordinaten des Endpunktes abziehen.
Der Vektor ![]() mit dem Anfangspunkt
mit dem Anfangspunkt ![]() und dem Endpunkt
und dem Endpunkt ![]() berechnet sich folgendermaßen:
berechnet sich folgendermaßen:
![]()
Es werden die Koordinaten der Pfeilspitze (Endpunkt) minus die Koordinaten vom Fuß (Anfangspunkt) des Vektors berechnet. Da der Vektorpfeil die beiden Punkte verbindet, heißt er auch Verbindungsvektor.
Beachte: Beim Berechnen musst du immer auf die Richtung des Vektors achten. Ist der Anfangspunkt des Vektors der Punkt ![]() , handelt es sich um den Vektor
, handelt es sich um den Vektor ![]() . Dieser berechnet sich folgendermaßen:
. Dieser berechnet sich folgendermaßen:
![]()
Beispiel:
Gegeben sind der Anfangspunkt ![]() und der Endpunkt
und der Endpunkt ![]() . Der Vektor
. Der Vektor ![]() zwischen den beiden Punkten lautet dann:
zwischen den beiden Punkten lautet dann:

Lage von Vektoren zueinander
Wie zwei Geraden können auch zwei Vektoren verschieden zueinander liegen.

Parallel
Zeigt ein Vektor ![]() in die gleiche Richtung wie der Vektor
in die gleiche Richtung wie der Vektor ![]() , sind die beiden Vektoren parallel zueinander. Parallel zueinander sind sie auch, wenn sie in entgegengesetzte Richtungen zeigen.
, sind die beiden Vektoren parallel zueinander. Parallel zueinander sind sie auch, wenn sie in entgegengesetzte Richtungen zeigen.
Von den oben dargestellten Vektoren sind die Vektoren ![]() ,
, ![]() und
und ![]() parallel zueinander. Für
parallel zueinander. Für ![]() und
und ![]() gilt:
gilt:
![]()
Gegenvektor
Sind zwei Vektoren ![]() und
und ![]() parallel zueinander, gleich lang und zeigen in entgegengesetzte Richtungen, dann ist
parallel zueinander, gleich lang und zeigen in entgegengesetzte Richtungen, dann ist ![]() der Gegenvektor von
der Gegenvektor von ![]() (und
(und ![]() der Gegenvektor von
der Gegenvektor von ![]() ). Der Gegenvektor von
). Der Gegenvektor von ![]() ist gleich
ist gleich ![]() . Es gilt also:
. Es gilt also:
![]()
Senkrecht
Schneiden sich zwei Vektoren in einem ![]() -Winkel, stehen sie senkrecht aufeinander.
-Winkel, stehen sie senkrecht aufeinander.
Arten von Vektoren
Wir unterscheiden zwei Arten von Vektoren: die Ortsvektoren und die Richtungsvektoren. Die folgende Tabelle zeigt die wichtigsten Eigenschaften der beiden Vektorarten.
| Art des Vektors | Eigenschaften | Bezeichnung | Beispiel |
|---|---|---|---|
| Ortsvektor | Startpunkt ist immer im Ursprung. Er kann für jeden Punkt im Koordinatensystem gebildet werden. Der Ortsvektor besitzt die gleichen Koordinaten wie der Punkt selbst. |
Punkt: Ortsvektor: |
|
| Richtungsvektor (Verbindungsvektor) | Startpunkt an einem beliebigen Punkt | Er beinhaltet entweder den Start- und Endpunkt ( |
Punkte: Richtungsvektor: |
Länge eines Vektors
Jeder Vektor besitzt eine bestimmte Länge, die dem Betrag des Vektors entspricht. Ist ein Vektor  gegeben, dann lässt sich die Länge mit der folgenden Formel berechnen:
gegeben, dann lässt sich die Länge mit der folgenden Formel berechnen:
![]()
Um die Länge eines Vektors zu berechnen, werden die einzelnen Komponenten quadriert und dann wird die Wurzel aus der Summe der quadrierten Komponenten gezogen.
Für den zweidimensionalen Raum gehen wir genauso vor, die dritte Komponente fällt dann weg.
Ist der Betrag eines Vektors ![]() , heißt der Vektor normiert:
, heißt der Vektor normiert:
![]()
Beispiel:
Die Länge des Vektors  ist:
ist:
![]()
Vektorrechnung – Mathe
Die folgenden Abschnitte zeigen, wie du mit Vektoren rechnen kannst.
Vektoraddition und Vektorsubtraktion
Werden zwei Vektoren addiert oder subtrahiert, dann sprechen wir von der Vektoraddition beziehungsweise der Vektorsubtraktion. Die Vektoraddition und Vektorsubtraktion erfolgt komponentenweise.
Zwei Vektoren  und
und 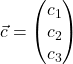 können folgendermaßen addiert und subtrahiert werden:
können folgendermaßen addiert und subtrahiert werden:
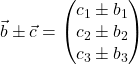
Es können auch mehr als zwei Vektoren addiert oder subtrahiert werden.
Beispiel:


Skalarmultiplikation
Um einen Vektor ![]() zu verlängern oder zu verkürzen, wird er mit einer reellen Zahl
zu verlängern oder zu verkürzen, wird er mit einer reellen Zahl ![]() multipliziert. Dabei werden alle Komponenten des Vektors einzeln mit
multipliziert. Dabei werden alle Komponenten des Vektors einzeln mit ![]() multipliziert. Die reelle Zahl wird auch als Skalar bezeichnet. Die Multiplikation mit einem Skalar wird Skalarmultiplikation genannt.
multipliziert. Die reelle Zahl wird auch als Skalar bezeichnet. Die Multiplikation mit einem Skalar wird Skalarmultiplikation genannt.

Dabei gilt:
- für
 , der Vektor wird gestaucht (verkürzt).
, der Vektor wird gestaucht (verkürzt). - für
 , der Vektor wird gestreckt (verlängert).
, der Vektor wird gestreckt (verlängert). - für
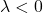 , die Richtung des Vektors wird geändert.
, die Richtung des Vektors wird geändert. - für
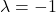 , der Gegenvektor wird gebildet.
, der Gegenvektor wird gebildet.
Beispiel:

Skalarprodukt
Bei dem Skalarprodukt handelt es sich um eine Abbildung, bei der aus zwei Vektoren eine reelle Zahl gebildet wird. Das Skalarprodukt darf nicht mit der Skalarmultiplikation verwechselt werden.
Sind zwei Vektoren  und
und 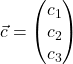 gegeben, dann ist das Skalarprodukt dieser zwei Vektoren definiert als:
gegeben, dann ist das Skalarprodukt dieser zwei Vektoren definiert als:

Stehen zwei Vektoren senkrecht aufeinander, ist das Skalarprodukt gleich ![]() . Wir können mit dem Skalarprodukt also berechnen, ob zwei Vektoren senkrecht aufeinander stehen.
. Wir können mit dem Skalarprodukt also berechnen, ob zwei Vektoren senkrecht aufeinander stehen.
Beispiel:

Kreuzprodukt
Bei der Berechnung des Kreuzprodukts zweier Vektoren erhalten wir einen Vektor, der senkrecht zu beiden Vektoren steht.
Sind zwei Vektoren  und
und 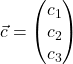 gegeben, dann berechnet sich das Kreuzprodukt als:
gegeben, dann berechnet sich das Kreuzprodukt als:

Beispiel:

Linearkombination
Als Linearkombination wird ein Vektor bezeichnet, der aus einer Kombination von Vektoraddition und Skalarmultiplikation entsteht. Es stellt eine Möglichkeit dar, aus zwei Vektoren einen neuen Vektor zu bilden. Die mathematische Schreibweise für die Linearkombination aus zwei Vektoren ist:
![]()
Dabei sind ![]() und
und ![]() reelle Zahlen, also Skalare.
reelle Zahlen, also Skalare. ![]() und
und ![]() sind die Vektoren, die kombiniert werden.
sind die Vektoren, die kombiniert werden.
Die mathematische Schreibweise für die Linearkombination aus drei Vektoren ist:
![]()
Dabei sind ![]() ,
, ![]() und
und ![]() reelle Zahlen, also Skalare.
reelle Zahlen, also Skalare. ![]() ,
, ![]() und
und ![]() sind die Vektoren, die kombiniert werden.
sind die Vektoren, die kombiniert werden.
Lineare Abhängigkeit
Lässt sich ein Vektor durch die Linearkombination eines anderen darstellen, dann sind die beiden Vektoren linear abhängig. Die Vektoren ![]() und
und ![]() sind linear abhängig, wenn gilt:
sind linear abhängig, wenn gilt:
![]()
Der Vektor ![]() ist dann ein Vielfaches des Vektors
ist dann ein Vielfaches des Vektors ![]() .
.
Grafisch zeigen diese Vektoren entweder in die gleiche oder in entgegengesetzte Richtung, müssen jedoch nicht gleich lang sein. Sie sind also parallel. Sind zwei Vektoren linear abhängig, heißen sie kollinear.
Liegen drei Vektoren im dreidimensionalen Raum in der gleichen Ebene, sind sie linear abhängig. Lässt sich ein Vektor als Linearkombination zweier anderer Vektoren darstellen, sind die drei Vektoren komplanar:
![]()
Dabei sind ![]() und
und ![]() reelle Zahlen. Der Vektor
reelle Zahlen. Der Vektor ![]() lässt sich als Linearkombination aus den Vektoren
lässt sich als Linearkombination aus den Vektoren ![]() und
und ![]() darstellen. Die drei Vektoren sind also komplanar.
darstellen. Die drei Vektoren sind also komplanar.
Lineare Unabhängigkeit
Zwei linear unabhängige Vektoren lassen sich nicht durch eine Linearkombination des jeweils anderen darstellen. Sie zeigen in zwei verschiedene Richtungen.
Drei Vektoren im dreidimensionalen Raum sind linear unabhängig, wenn sie paarweise unabhängig sind und einer der Vektoren aus der Ebene heraus zeigt, die die anderen beiden aufspannen.
Vektor zeichnen
Die Vorgehensweise, um einen Ortsvektor zu zeichnen, ist zunächst genauso wie beim Einzeichnen eines Punktes in ein Koordinatensystem. Soll der Vektor 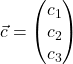 gezeichnet werden, gehen wir folgendermaßen vor:
gezeichnet werden, gehen wir folgendermaßen vor:
- Vom Ursprung
 Einheiten entlang der
Einheiten entlang der  -Achse gehen. Ist
-Achse gehen. Ist  positiv, gehen wir nach rechts, ist
positiv, gehen wir nach rechts, ist  negativ, gehen wir nach links.
negativ, gehen wir nach links. - Im Anschluss
 Einheiten in
Einheiten in  -Richtung gehen. Ist
-Richtung gehen. Ist  positiv, gehen wir nach oben, ist
positiv, gehen wir nach oben, ist  negativ, gehen wir nach unten.
negativ, gehen wir nach unten. - Dann
 Einheiten in
Einheiten in  -Richtung gehen. Ist
-Richtung gehen. Ist  positiv, gehen wir nach vorne, ist
positiv, gehen wir nach vorne, ist  negativ, gehen wir nach hinten.
negativ, gehen wir nach hinten. - So erhalten wir den Endpunkt des Vektors.
- Endpunkt mit dem Ursprung verbinden. Die Pfeilspitze wird am Endpunkt eingezeichnet.
Da ein Vektor durch seine Richtung und seine Länge, jedoch nicht durch seinen Startpunkt eindeutig definiert ist, ist es egal, wo wir beim Einzeichnen eines Richtungsvektors starten. Für den gleichen Vektor gibt es also unendlich viele Möglichkeiten, ihn einzuzeichnen.
Im zweidimensionalen Raum funktioniert das genauso, dort gibt es bloß keine ![]() -Achse und die Vektoren haben dementsprechend nur zwei Koordinaten.
-Achse und die Vektoren haben dementsprechend nur zwei Koordinaten.
Vektoren ablesen
Um die Koordinaten eines Vektors abzulesen, starten wir beim Anfangspunkt des Vektors. Dann muss nachgezählt werden, um wie viele Einheiten der Endpunkt in Richtung der ![]() -Achse, in Richtung der
-Achse, in Richtung der ![]() -Achse und in Richtung der
-Achse und in Richtung der ![]() -Achse zum Anfangspunkt verschoben ist. Die Verschiebung in Richtung der
-Achse zum Anfangspunkt verschoben ist. Die Verschiebung in Richtung der ![]() -Achse bildet die erste Koordinate, die Verschiebung in Richtung der
-Achse bildet die erste Koordinate, die Verschiebung in Richtung der ![]() -Achse die zweite Koordinate und die Verschiebung in Richtung der
-Achse die zweite Koordinate und die Verschiebung in Richtung der ![]() -Achse die dritte Koordinate des Vektors.
-Achse die dritte Koordinate des Vektors.
Im zweidimensionalen Raum funktioniert das genauso, dort gibt es bloß keine ![]() -Achse und die Vektoren haben dementsprechend nur zwei Koordinaten.
-Achse und die Vektoren haben dementsprechend nur zwei Koordinaten.
Hinweis: Im dreidimensionalen Koordinatensystem ist die Darstellung nicht eindeutig. Die Komponenten eines Vektors können nur dann eindeutig abgelesen werden, wenn zusätzliche Informationen bekannt sind.
Häufig gestellte Fragen zum Thema Vektoren in Mathe

