Trapez – Definition, Flächeninhalt und Umfang

Das Trapez ist eine geometrische Form, definiert als ein Viereck mit zwei parallelen Seiten. Es gibt verschiedene Arten von Trapezen. Einige Beispiele sind:

• Allgemeines Trapez: Alle Seiten sind verschieden lang, alle Winkel sind verschieden groß.
• Symmetrisches oder gleichschenkliges Trapez: Die nicht parallelen Seiten sind gleich lang, das Trapez ist achsensymmetrisch.
• Rechtwinkliges Trapez: Es besitzt einen rechten Winkel.

Rechtecke, Quadrate und Parallelogramme erfüllen ebenfalls die Bedingung für Trapeze. Somit gilt: Jedes Rechteck, jedes Quadrat und jedes Parallelogramm ist ein Trapez. 

Ein Trapez kann also sehr verschiedene Formen haben, solange es vier Ecken und mindestens ein paralleles Seitenpaar besitzt.

Wie bei jedem Viereck werden die vier Seiten des Trapezes mit , , und beschriftet. Die Ecken werden gegen den Uhrzeigersinn als , , und bezeichnet. Bei der Ecke liegt der Winkel , bei der Winkel , bei der Winkel und bei der Winkel .

Die zueinander parallelen Seiten werden als Grundseiten bezeichnet. Die anderen beiden Seiten nennen wir Schenkel.

Trapeze weisen bestimmte Besonderheiten und Merkmale auf. Diese sind:

• Der Abstand zwischen den beiden Grundseiten (parallelen Seiten) ist die Höhe 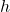des Trapezes.
• Werden die beiden Mittelpunkte der Schenkel miteinander verbunden, entsteht eine zu den Grundseiten parallele Linie. Diese wird Mittellinie 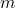genannt und ist halb so lang wie die Summe der beiden Grundseiten:
  
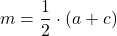
• Die Innenwinkelsumme eines Trapezes ist immer :
  
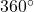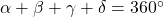
• Die an einem Schenkel anliegenden Winkel ergeben zusammen immer :
  

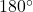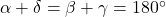
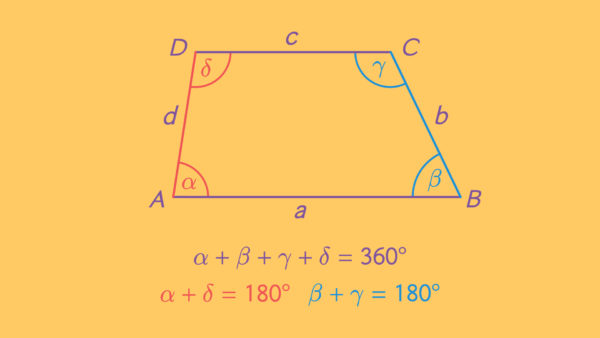
Alle diese Eigenschaften treffen auf das allgemeine Trapez sowie alle anderen Formen von Trapezen zu. Für gleichschenklige Trapeze (Schenkel sind gleich lang) gilt zudem:

• Gleichschenklige Trapeze sind achsensymmetrisch. Die Mittelsenkrechte der beiden Grundseiten des Trapezes bildet dabei die Symmetrieachse.

Die Summe aller vier Seitenlängen eines Vierecks ist der Umfang . Das ist die Strecke, die du laufen müsstest, um das Viereck einmal zu umrunden. Auch bei einem Trapez ergibt sich der Umfang als Summe der Seitenlängen, da es sich um ein spezielles Viereck handelt.

Die Seiten eines Trapezes werden mit , , und bezeichnet. Da der Umfang die Summe der vier Seitenlängen ist, berechnet sich der Umfang eines Trapezes mit der Formel:

Diese Formel gilt für jede Trapezform.
Fehlende Seiten von Trapezen können mithilfe des Umfangs berechnet werden. Dafür muss die Formel für den Umfang nach der gesuchten Seite umgestellt werden. Ist die Seite gesucht, lautet die Formel:

Betrachten wir ein Trapez mit den Seitenlängen:

Der Umfang vom Trapez beträgt:

Wie viel Fläche ein Trapez einnimmt, wird durch seinen Flächeninhalt angegeben. Er wird in Flächeneinheiten wie (Quadratkilometer), (Quadratmeter) oder (Quadratzentimeter) angegeben.

Für die Berechnung des Flächeninhalts eines Trapezes wird seine Höhe benötigt. Der Abstand zwischen den beiden parallelen Seiten wird als Höhe bezeichnet. Sie steht immer senkrecht auf den parallelen Seiten. Sind und die parallelen Seiten, ist die Formel für den Flächeninhalt:

Mit dieser Formel wird auch der Flächeninhalt gleichschenkliger Trapeze berechnet.

Für die Herleitung der Formel des Flächeninhalts eines Trapezes schauen wir uns die Geometrie des Trapezes an.
Dafür verdoppeln wir zunächst das Trapez und legen die Kopie um gedreht an das ursprüngliche Trapez an. So entsteht ein Parallelogramm, dessen horizontale Seiten die Länge besitzen.

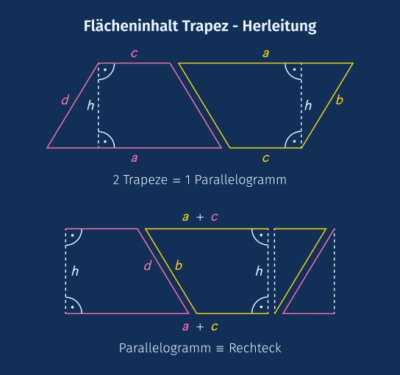
Dann trennen wir auf der linken Seite entlang der Höhe ein Dreieck ab und legen es rechts an. Es entsteht ein Rechteck mit der horizontalen Seitenlänge und der vertikalen Seitenlänge . Der Flächeninhalt des Rechtecks ist somit .
Bei dem Rechteck handelt es sich um eine Verdopplung des Trapezes. Demnach ist der Flächeninhalt des Trapezes halb so groß. Wir erhalten die bekannte Formel:

Betrachten wir ein Trapez, dessen parallelen Seiten die Längen und haben. Die Höhe dieses Trapezes ist . Eingesetzt in die Formel erhalten wir mithilfe dieser Werte den Flächeninhalt:

Denk immer daran, die Einheit des Flächeninhalts zu beachten.

Um ein Trapez konstruieren zu können, müssen mindestens vier geeignete Größen gegeben sein. Das können zum Beispiel zwei Winkel und zwei Seiten oder eine Seite, die Höhe und zwei Winkel sein.
Schauen wir uns die Konstruktion eines Trapezes gemeinsam an einem Beispiel an:

Gegeben:

Schritt 1:
Zunächst kannst du eine Skizze von deinem Trapez zeichnen. Es kann helfen, in der Skizze die gegebenen Größen farbig zu markieren.

Schritt 2:
Nun kannst du die Seite mit einem Lineal oder Geodreieck zeichnen. Sie wird durch die Punkte (links) und (rechts) begrenzt. Im Punkt kannst du mit einem Geodreieck den Winkel und im Punkt den Winkel abtragen.

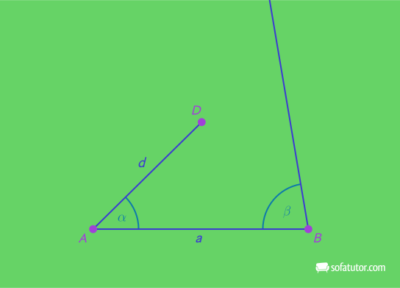
Schritt 3:
Auf der Halbgeraden, die im Punkt startet, kannst du die Länge der Seite abtragen. Du erhältst den Punkt .

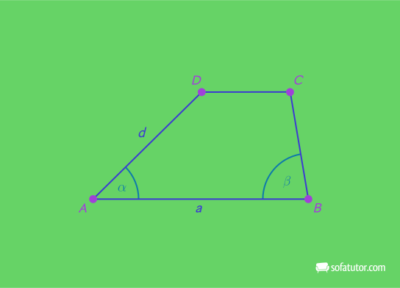
Schritt 4:
Du siehst bereits, dass die Seite und die Seite nicht parallel zueinander sein können. Also muss es eine zu parallele Seite geben. Mithilfe einer Parallelverschiebung der Seite zum Punkt erhältst du die Seite . Dort, wo diese die Halbgerade aus schneidet, liegt der Punkt .