Die Mitternachtsformel zum Lösen von quadratischen Gleichungen – Erklärung

Erfahre, wie die Mitternachtsformel als wichtige Lösungsformel für quadratische Gleichungen funktioniert. Entdecke, warum sie auch als „Mitternachtsformel“ bekannt ist und wie sie mit der Diskriminante zusammenhängt. Dies und vieles mehr findest du im folgenden Text.

Inhaltsverzeichnis zum Thema Mitternachtsformel

Die Mitternachtsformel im Überblick

  • Die Mitternachtsformel ist eine Lösungsformel für quadratische Gleichungen.

  • Der Name Mitternachtsformel kommt daher, dass die Formel in Mathe so wichtig ist, dass du sie so gut auswendig kennen solltest, dass du sie auch aufsagen kannst, wenn du um Mitternacht geweckt wirst.

  • Ein anderer Name für die Mitternachtsformel ist abc-Formel.

  • Die pq-Formel ist eine weitere Lösungsformel für quadratische Gleichungen.

Mitternachtsformel Video

Quelle sofatutor.com

Mitternachtsformel einfach erklärt

Die Mitternachtsformel ist eine Lösungsformel für quadratische Gleichungen mit Parametern a, b und c der Form:
ax^2+bx+c=0, \quad a\neq0
Sie lautet:
x_{1,2} = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}

Beispiel:
Die quadratische Gleichung 2x^2+5x+2 = 0 soll gelöst werden. Hier sind also a=2, b=5 und c=2. Diese setzen wir in die Mitternachtsformel ein und können dann auflösen:
x_{1,2} = \dfrac{-5\pm\sqrt{5^2-4\cdot2\cdot2}}{2\cdot2}
x_{1,2} = \dfrac{-5\pm\sqrt{25-16}}{4}
x_{1,2} = \dfrac{-5\pm\sqrt{9}}{4}
x_{1,2} = \dfrac{-5\pm3}{4}
Die Lösungen der Gleichung lauten x_1 = \dfrac{-5-3}{4} = \dfrac{-8}{4}=-2 und x_2 = \dfrac{-5+3}{4} = \dfrac{-2}{4}=-\dfrac{1}{2}.

Mitternachtsformel und Diskriminante

Schauen wir uns nun den Term der Mitternachtsformel einmal genauer an: Im Zähler steht ein Wurzelterm. Als solcher ist er nur definiert, wenn der Wert unter der Wurzel größer oder gleich null ist.
Dies hat Auswirkungen auf die Lösbarkeit der quadratischen Gleichung: Ist der Term unter der Wurzel größer als null, hat die quadratische Gleichung zwei Lösungen. Ist der Term kleiner als null, ist die Wurzel nicht definiert und das bedeutet, dass die quadratische Gleichung keine Lösung hat. Ist der Term gleich null, hat die quadratische Gleichung eine Lösung, denn die Fallunterscheidung, die durch das \pm entsteht, fällt weg.

Weil der Term unter der Wurzel b^2-4ac für die Lösbarkeit ausschlaggebend ist, hat dieser sogar einen eigenen Namen bekommen. Er heißt Diskriminante und wird oft kurz D = b^2-4ac geschrieben. In der folgenden Tabelle sind die verschiedenen Fälle für die Diskriminante zusammengefasst.

D = b^2-4ac Bedeutung für die Lösbarkeit der Gleichung
ax^2+bx+c=0
D > 0 Die Gleichung besitzt zwei Lösungen, die mit der Mitternachtsformel bestimmt werden.
D = 0 Die Gleichung besitzt eine Lösung: x = \dfrac{-b}{2a}.
D<0 Die Gleichung hat keine Lösung.

Mitternachtsformel – Herleitung

Zum Beweis der Mitternachtsformel nehmen wir die allgemeine quadratische Gleichung in der Form ax^2+bx+c=0 und formen sie mit Äquivalenzumformungen um. Dabei wird geschickt umgeformt, um auf der linken Seite die binomische Formel anwenden zu können und dann die Wurzel zu ziehen.

\begin{array}{rcll} ax^2+bx+c & = & 0 & \vert -c\\ ax^2+bx &=&-c & \vert \cdot 4a\\ 4a^2x^2 +4abx & = & -4ac & \vert +b^2\\ 4a^2x^2 +4abx + b^2 & = & b^2 - 4ac & \vert \text{binomische Formel auf der linken Seite}\\ (2ax + b)^2 & = & b^2-4ac & \vert \text{Wurzel ziehen} \\ 2ax + b &=& \pm \sqrt{b^2-4ac} & \vert -b \\ 2ax & = & -b\pm\sqrt{b^2-4ac} & \vert :2a \\ x & = & \dfrac{-b \pm\sqrt{b^2-4ac} }{2a} & \end{array}

Beim Wurzelziehen kann das Ergebnis positiv oder negativ sein, deswegen kommt in dem entsprechenden Schritt das Vorzeichen \pm zustande. Dementsprechend gibt es im Allgemeinen auch zwei Lösungen x_{1,2}.

Mitternachtsformel und 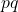pq-Formel

Die pq-Formel ist ebenfalls eine bekannte Lösungsformel für quadratische Gleichungen. Der Unterschied zur Mitternachtsformel ist, dass die Gleichung in Normalform vorliegen muss. Das bedeutet, dass der Koeffizient vor dem x^2, also a, gleich 1 sein muss. Außerdem heißen die anderen beiden Quotienten p und q statt b und c. Die folgende Tabelle fasst die Unterschiede zwischen Mitternachtsformel und pq-Formel zusammen.

Formel Mitternachtsformel pq-Formel
anwendbar auf quadratische Gleichungen in allgemeiner Form:
ax^2+bx+c=0, a\neq0		 quadratische Gleichungen in Normalform:
x^2+px+q=0
Lösungsformel x_{1,2} = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a} x_{1,2} =-\dfrac{1}{2}\pm\sqrt{\left(\dfrac{1}{2}\right)^2-q}

Mitternachtsformel und Nullstellen

Wenn für eine quadratische Funktion f mit f(x) = ax^2 +bx+c die Nullstellen bestimmt werden sollen, ist das gleichbedeutend damit, dass die quadratische Gleichung ax^2 +bx+c = 0 gelöst werden muss. Hier kann uns also die Mitternachtsformel ebenfalls helfen.

Die Fallunterscheidung für die Diskriminante D = b^2-4ac hat in diesem Fall eine Bedeutung für die Anzahl der Nullstellen der Funktion f:

D > 0: Die Funktion f hat zwei Nullstellen.
D = 0: Die Funktion f hat eine Nullstelle. Diese Nullstelle ist gleichzeitig der Scheitelpunkt der Funktion. In diesem Fall können wir mit der Mitternachtsformel also sogar den Scheitelpunkt von einer Parabel bestimmen.
D<0: Die Funktion f hat keine Nullstelle.

Beispiel:
Gegeben ist die Parabel f mit der Funktionsgleichung f(x) = 2x^2 - 4x +2. Von dieser Funktion möchten wir Nullstellen bestimmen. Dafür setzen wir die Funktionsgleichung gleich null:
2x^2-4x+2 = 0
Die Lösung dieser Gleichung können wir nun mithilfe der Mitternachtsformel finden. Die Parameter lauten in diesem Fall a=2, b=-4 und c=2. Diese Werte setzen wir ein und erhalten:
x_{1,2} = \dfrac{-(-4)\pm\sqrt{(-4)^2-4\cdot2\cdot2}}{2\cdot2}= \dfrac{4\pm\sqrt{16-16}}{4} = \dfrac{4\pm0}{4}=1
Wir stellen fest, dass in diesem Fall die Diskriminante D = b^2-4ac = 0 ist. Das bedeutet, dass die Funktion nur eine Nullstelle bei x=1 besitzt. Diese ist gleichzeitig der Scheitelpunkt S(1|0).

Ähnlich kann dir die Mitternachtsformel auch bei der Nullstellenbestimmung von achsensymmetrische Funktionen vierten Grads der Form f(x) = ax^4 + bx^2 + c helfen. Durch Substitution von x^2 = z erhalten wir eine quadratische Gleichung, lösen diese mit der Mitternachtsformel und erhalten durch Rücksubstitution und Wurzelziehen alle Nullstellen der Funktion.

Häufig gestellte Fragen zum Thema Mitternachtsformel

Die Mitternachtsformel hilft beim Lösen von quadratischen Gleichungen. 

Der Name der Mitternachtsformel wurde angeblich erfunden, weil sie so wichtig ist, dass du sie aufsagen können solltest, wenn du um Mitternacht geweckt wirst.

Mit der Mitternachtsformel werden Lösungen einer quadratischen Gleichung der Form ax^2 + bx + c = 0 berechnet.

Liegt eine quadratische Gleichung in der Form ax^2+bx+c = 0 mit a\neq0 vor, so gibt die Mitternachtsformel die Lösungen dieser Gleichung an. Ausgeschrieben lautet die Mitternachtsformel:
x_{1,2}=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}

Die Mitternachtsformel lautet:
x_{1,2}=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
Sie gibt damit Lösungen der quadratischen Gleichung in der Form ax^2+bx+c = 0 mit a\neq0 an.

Die Mitternachtsformel wird zum Berechnen von Lösungen von quadratischen Gleichungen genutzt. 

Beide Formeln helfen beim Lösen von quadratischen Gleichungen. Zum Anwenden der Mitternachtsformel muss die Gleichung in der allgemeinen Form ax^2+bx+c=0, a\neq0 vorliegen. Für die pq-Formel muss die Gleichung die Normalform x^2+px+q = 0 haben, der Koeffizient vor dem Term x^2 muss also 1 sein.

Du kannst die Mitternachtsformel anwenden, wenn du eine quadratische Gleichung in der Form ax^2+bx+c=0, a\neq0 vorliegen hast und die Lösungen dieser Gleichung suchst.

Die Mitternachtsformel ist eine Lösungsformel für quadratische Gleichungen.

Die Herleitung der Mitternachtsformel kann durch Termumformungen ausgehend von der Gleichung ax^2+bx+c=0, a\neq0 durchgeführt werden.

Die Mitternachtsformel kann auch bei quadratischen Ungleichungen angewendet werden. Hierfür wird in der Ungleichung zunächst das Relationszeichen durch ein = ersetzt und die Mitternachtsformel wie gehabt angewendet. Aus den beiden Lösungen x_1 und x_2 ergibt sich dann die Lösungsmenge: entweder alle Zahlen zwischen x_1 und x_2 oder alle Zahlen außerhalb dieses Intervalls.

Die Mitternachtsformel gilt auch für quadratische Gleichungen mit komplexen Koeffizienten. 

Leave A Comment

Alle Artikel aus dem Fach Mathematik