Wurzel ziehen in der Mathematik – Definition, Beispiele und Anwendungen
Erfahre, wie das Wurzelziehen in der Mathematik funktioniert und was es bedeutet, eine Wurzel zu lösen. Entdecke Eigenschaften von Quadratwurzeln und höheren Wurzeln sowie deren praktische Anwendungen, z.B. beim Lösen quadratischer Gleichungen und im Satz des Pythagoras.
Inhaltsverzeichnis zum Thema Wurzel ziehen
Wurzel ziehen im Überblick
Wurzeln in der Mathematik – Definition und Eigenschaften
In der Mathematik kommen verschiedene Wurzeln vor. Am häufigsten verwendet werden die Quadratwurzeln, die auch einfach als Wurzeln bezeichnet werden. Das Wurzelziehen ist die Umkehroperation des Quadrierens bzw. des Potenzierens. Wurzeln zu höheren Potenzen werden z. B. als dritte Wurzel, vierte Wurzel oder ![]() -te Wurzel bezeichnet.
-te Wurzel bezeichnet.
Quadratwurzeln – Definition und Eigenschaften
Du kennst bestimmt schon die Folge der Quadratzahlen. Diese erhältst du, indem du die natürlichen Zahlen quadrierst: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() und so weiter. Beim Wurzelziehen drehen wir die Operation des Quadrierens um. Gesucht ist also nicht wie beim Quadrieren eine Zahl
und so weiter. Beim Wurzelziehen drehen wir die Operation des Quadrierens um. Gesucht ist also nicht wie beim Quadrieren eine Zahl ![]() , die das Quadrat einer gegebenen Zahl
, die das Quadrat einer gegebenen Zahl ![]() ist, sondern umgekehrt: Gesucht ist eine Zahl
ist, sondern umgekehrt: Gesucht ist eine Zahl ![]() , deren Quadrat die vorgegebene Zahl
, deren Quadrat die vorgegebene Zahl ![]() ist.
ist.
Am einfachsten erklärt wird das Wurzelziehen am Beispiel der Quadratzahlen: Die Wurzel aus der Zahl ![]() ist eine Zahl
ist eine Zahl ![]() , deren Quadrat die Zahl
, deren Quadrat die Zahl ![]() ergibt:
ergibt: ![]() . Wir kennen eine solche Zahl, nämlich
. Wir kennen eine solche Zahl, nämlich ![]() . Denn
. Denn ![]() . Also schreiben wir:
. Also schreiben wir:
![]()
Aber was ist mit der Zahl ![]() ? Es gilt auch
? Es gilt auch ![]() . Die gesuchte Zahl
. Die gesuchte Zahl ![]() mit der Eigenschaft, dass
mit der Eigenschaft, dass ![]() gilt, ist also nicht eindeutig. Ganz allgemein gilt: Zu jeder Zahl
gilt, ist also nicht eindeutig. Ganz allgemein gilt: Zu jeder Zahl ![]() mit
mit ![]() können wir auch die Gegenzahl
können wir auch die Gegenzahl ![]() verwenden. Denn mit
verwenden. Denn mit ![]() gilt auch
gilt auch ![]() .
.
Definition
Um mit der Uneindeutigkeit der Lösungen ![]() und
und ![]() der Gleichung
der Gleichung ![]() umzugehen, verwenden wir die folgende Definition der Wurzel: Die Wurzel
umzugehen, verwenden wir die folgende Definition der Wurzel: Die Wurzel ![]() einer Zahl
einer Zahl ![]() ist die eindeutig bestimmte positive Lösung der Gleichung
ist die eindeutig bestimmte positive Lösung der Gleichung ![]() . Die Gleichung
. Die Gleichung ![]() hat auch eine negative Lösung. Die negative Lösung ist die Gegenzahl der positiven Lösung. Daher schreiben wir
hat auch eine negative Lösung. Die negative Lösung ist die Gegenzahl der positiven Lösung. Daher schreiben wir ![]() für die eindeutig bestimmte negative Lösung der Gleichung
für die eindeutig bestimmte negative Lösung der Gleichung ![]() .
.
Für ![]() ist also
ist also ![]() , denn
, denn ![]() und
und ![]() . Außerdem ist
. Außerdem ist ![]() , denn
, denn ![]() ist die Gegenzahl von
ist die Gegenzahl von ![]() .
.
Ist ![]() , ist die Gleichung
, ist die Gleichung ![]() eindeutig lösbar durch
eindeutig lösbar durch ![]() . Wir schreiben daher auch
. Wir schreiben daher auch ![]() . Ist
. Ist ![]() , hat die Gleichung
, hat die Gleichung ![]() gar keine reelle Zahl
gar keine reelle Zahl ![]() als Lösung. Denn das Quadrat einer reellen Zahl
als Lösung. Denn das Quadrat einer reellen Zahl ![]() ist niemals negativ.
ist niemals negativ.
Eigenschaften
- Eine Zahl und ihre Gegenzahl haben dasselbe Quadrat. Die Wurzel aus einer Quadratzahl ist immer die positive der beiden Zahlen mit diesem Quadrat. Es ist also
 , denn
, denn 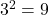 und
und 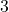 ist positiv.
ist positiv. - Quadrierst du eine Wurzel, erhältst du immer die Zahl unter der Wurzel:
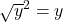 . Denn
. Denn  ist die eindeutige Lösung der Gleichung
ist die eindeutige Lösung der Gleichung 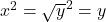 .
. - Ziehst du die Wurzel aus dem Quadrat einer Zahl
 , erhältst du nicht automatisch die Zahl
, erhältst du nicht automatisch die Zahl  , die du quadriert hast. Denn
, die du quadriert hast. Denn  kann eine negative Zahl sein, aber die Wurzel ist nie negativ. Statt der Zahl
kann eine negative Zahl sein, aber die Wurzel ist nie negativ. Statt der Zahl  erhältst du beim Wurzelziehen aus
erhältst du beim Wurzelziehen aus 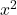 im Allgemeinen den Betrag von
im Allgemeinen den Betrag von  . Es gilt also:
. Es gilt also:  . Beispielsweise ist
. Beispielsweise ist  , sondern
, sondern  .
.
Damit wir über die Eigenschaften des Wurzelziehens einfacher sprechen können, bezeichnen wir die einzelnen Zahlen, die dabei vorkommen, mit Fachausdrücken: Die Zahl unter der Wurzel heißt Radikand. Das Ergebnis des Wurzelziehens ist der Wurzelwert. Und die Zahl ![]() im Exponenten der Gleichung nennt man Wurzelexponenten. Bei Quadratwurzeln lässt man den Exponenten
im Exponenten der Gleichung nennt man Wurzelexponenten. Bei Quadratwurzeln lässt man den Exponenten ![]() meistens weg und schreibt einfach
meistens weg und schreibt einfach ![]() statt
statt ![]() .
.
Deutlicher wird das noch im folgenden Abschnitt, wenn wir Wurzeln mit höheren Exponenten betrachten.
Wurzeln höherer Exponenten – Definition und Eigenschaften
Die Quadratwurzel einer Zahl ![]() ist die eindeutige positive Lösung
ist die eindeutige positive Lösung ![]() der Gleichung
der Gleichung ![]() . Das Wurzelziehen macht in einem bestimmten Sinn das Quadrieren rückgängig: Ist
. Das Wurzelziehen macht in einem bestimmten Sinn das Quadrieren rückgängig: Ist ![]() , ist
, ist ![]() . Wenn du eine positive Zahl
. Wenn du eine positive Zahl ![]() quadrierst und dann daraus die Wurzel ziehst, erhältst du wieder die Zahl
quadrierst und dann daraus die Wurzel ziehst, erhältst du wieder die Zahl ![]() .
.
Statt eine Zahl ![]() nur zu quadrieren, können wir auch eine höhere Potenz der Zahl berechnen. Wollen wir diese Operation des Potenzierens umkehren, benötigen wir Wurzeln zu höheren Exponenten. Wir beschränken uns dabei wieder auf den Fall
nur zu quadrieren, können wir auch eine höhere Potenz der Zahl berechnen. Wollen wir diese Operation des Potenzierens umkehren, benötigen wir Wurzeln zu höheren Exponenten. Wir beschränken uns dabei wieder auf den Fall ![]() .
.
Bei Wurzeln mit höherem Exponenten müssen wir unterscheiden zwischen geraden und ungeraden Wurzelexponenten:
n-te Wurzeln für gerades n
Ist ![]() eine gerade Zahl, z. B.
eine gerade Zahl, z. B. ![]() ,
, ![]() usw., ist die
usw., ist die ![]() -te Wurzel ganz analog definiert wie bei Quadratwurzeln: Die
-te Wurzel ganz analog definiert wie bei Quadratwurzeln: Die ![]() -te Wurzel einer Zahl
-te Wurzel einer Zahl ![]() ist die eindeutige positive Lösung
ist die eindeutige positive Lösung ![]() der Gleichung
der Gleichung ![]() . Die Zahl
. Die Zahl ![]() unter der Wurzel heißt Radikand. Die Zahl
unter der Wurzel heißt Radikand. Die Zahl ![]() auf dem Wurzelzeichen bzw. im Exponenten der Gleichung heißt Wurzelexponent. Die Zahl
auf dem Wurzelzeichen bzw. im Exponenten der Gleichung heißt Wurzelexponent. Die Zahl ![]() schließlich ist der Wurzelwert.
schließlich ist der Wurzelwert.
Beispielsweise ist ![]() . Denn
. Denn ![]() . Die Zahl
. Die Zahl ![]() ist der Wurzelexponent und der Exponent der zugehörigen Gleichung ohne Wurzel. Die Zahl
ist der Wurzelexponent und der Exponent der zugehörigen Gleichung ohne Wurzel. Die Zahl ![]() ist der Radikand, also die Zahl, aus der die vierte Wurzel gezogen wird. Der Wurzelwert ist in diesem Beispiel die Zahl
ist der Radikand, also die Zahl, aus der die vierte Wurzel gezogen wird. Der Wurzelwert ist in diesem Beispiel die Zahl ![]() .
.
Die Gleichung ![]() hat im Fall, dass
hat im Fall, dass ![]() gerade ist, zwei verschiedene Lösungen, nämlich
gerade ist, zwei verschiedene Lösungen, nämlich ![]() und
und ![]() . Die
. Die ![]() -Wurzel ist definiert als die positive Lösung dieser Gleichung und nur durch diese zusätzliche Bedingung eindeutig bestimmt. Anders ist die Situation für ungerade Wurzelexponenten, die wir uns im nächsten Abschnitt ansehen:
-Wurzel ist definiert als die positive Lösung dieser Gleichung und nur durch diese zusätzliche Bedingung eindeutig bestimmt. Anders ist die Situation für ungerade Wurzelexponenten, die wir uns im nächsten Abschnitt ansehen:
n-te Wurzeln für ungerades n
Ist ![]() eine ungerade Zahl, z. B.
eine ungerade Zahl, z. B. ![]() ,
, ![]() ,
, ![]() usw., hat die Gleichung
usw., hat die Gleichung ![]() stets nur eine reelle Zahl als Lösung. Wir müssen also das Vorzeichen dieser Lösung nicht eigens wählen. Wir definieren daher
stets nur eine reelle Zahl als Lösung. Wir müssen also das Vorzeichen dieser Lösung nicht eigens wählen. Wir definieren daher ![]() als die eindeutige Lösung
als die eindeutige Lösung ![]() der Gleichung
der Gleichung ![]() .
.
Beispielsweise ist ![]() . Denn
. Denn ![]() . Die Zahl
. Die Zahl ![]() ist der Wurzelexponent und der Exponent der zugehörigen Gleichung ohne Wurzel. Die Zahl
ist der Wurzelexponent und der Exponent der zugehörigen Gleichung ohne Wurzel. Die Zahl ![]() ist der Radikand, also die Zahl, aus der die dritte Wurzel gezogen wird. Der Wurzelwert ist in diesem Beispiel die Zahl
ist der Radikand, also die Zahl, aus der die dritte Wurzel gezogen wird. Der Wurzelwert ist in diesem Beispiel die Zahl ![]() .
.
Die Tatsache, dass die Gleichung ![]() für ungerade Exponenten eindeutig lösbar ist, gilt aber nicht nur für
für ungerade Exponenten eindeutig lösbar ist, gilt aber nicht nur für ![]() , sondern auch für negative Radikanden
, sondern auch für negative Radikanden ![]() . Die
. Die ![]() -te Wurzel
-te Wurzel ![]() ist daher auch für Radikanden
ist daher auch für Radikanden ![]() definiert. Der Wurzelwert hat das gleiche Vorzeichen wie der Radikand: Ist
definiert. Der Wurzelwert hat das gleiche Vorzeichen wie der Radikand: Ist ![]() , ist auch
, ist auch ![]() .
.
Dass die Gleichung ![]() für ungerade Exponenten eindeutig lösbar ist, kann man auch noch anders ausdrücken: Ist
für ungerade Exponenten eindeutig lösbar ist, kann man auch noch anders ausdrücken: Ist ![]() eine Lösung der Gleichung
eine Lösung der Gleichung ![]() , ist die Gegenzahl
, ist die Gegenzahl ![]() keine Lösung dieser Gleichung: Denn für die Gegenzahl
keine Lösung dieser Gleichung: Denn für die Gegenzahl ![]() gilt:
gilt: ![]() . Hierbei haben wir benutzt, dass
. Hierbei haben wir benutzt, dass ![]() ist, wenn der Exponent
ist, wenn der Exponent ![]() ungerade ist.
ungerade ist.
Quadratwurzeln und Wurzeln höherer Exponenten – Exponentialschreibweise
Da das Wurzelziehen das Quadrieren bzw. Potenzieren umkehrt, kannst du die Exponentialschreibweise benutzen, um Wurzeln darzustellen. Die Quadratwurzel einer Zahl ![]() schreibst du dann als Potenz mit dem Exponenten
schreibst du dann als Potenz mit dem Exponenten ![]() , also
, also ![]() . Analog schreibst du die
. Analog schreibst du die ![]() -Wurzel von
-Wurzel von ![]() als Potenz mit dem Exponenten
als Potenz mit dem Exponenten ![]() , also
, also ![]() .
.
Der Grund für diese Schreibweise liegt in den Potenzgesetzen: Für natürliche Zahlen ![]() und
und ![]() als Exponenten gilt
als Exponenten gilt ![]() . Diese Schreibweise wird auf positive rationale Zahlen als Exponenten erweitert. Die Stammbrüche als Exponenten entsprechen dann genau den höheren Wurzeln. Denn wegen der Potenzregel ist
. Diese Schreibweise wird auf positive rationale Zahlen als Exponenten erweitert. Die Stammbrüche als Exponenten entsprechen dann genau den höheren Wurzeln. Denn wegen der Potenzregel ist ![]() eine positive Zahl, für die gilt:
eine positive Zahl, für die gilt: ![]() . Also muss
. Also muss ![]() sein, denn
sein, denn ![]() ist die eindeutige positive Lösung der Gleichung
ist die eindeutige positive Lösung der Gleichung ![]() .
.
Das Analoge gilt auch für Wurzeln mit höheren Exponenten: Die Zahl ![]() erfüllt die Gleichung
erfüllt die Gleichung ![]() . Also ist
. Also ist ![]() und folglich
und folglich ![]() .
.
Wurzeln in der Mathematik – Rechenregeln und Wurzelgesetze
Die wichtigsten Rechenregeln beim Rechnen mit Wurzeln sind die folgenden:
Quadratwurzeln spezieller Zahlen
- Die Wurzel aus einer Quadratzahl ist die natürliche Zahl, deren Quadrat die vorgegebene Quadratzahl ist. Beispielsweise ist
 , denn
, denn 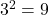 .
. - Ist
 keine Quadratzahl, ist
keine Quadratzahl, ist  keine ganze Zahl.
keine ganze Zahl. 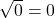 und
und ![Rendered by QuickLaTeX.com \sqrt[n]{0}=0](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-2bd72760736459c91127490ff6d2af76_l3.png) , denn
, denn 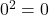 und
und  .
. und
und ![Rendered by QuickLaTeX.com \sqrt[n]{1}=1](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-59456728d9871ac006e9fce38773e32b_l3.png) , denn
, denn  und
und  .
.- Die Wurzel aus einer negativen Zahl existiert nicht (bzw. ist keine reelle Zahl).
Rechenregeln für Wurzeln und Quadrate
- Das Quadrat einer Wurzel ist die Zahl unter der Wurzel:
 .
. - Die Wurzel aus dem Quadrat einer Zahl ist der Betrag dieser Zahl:
 .
.
Wurzeln aus Produkten und Quotienten
- Die Wurzel aus dem Produkt zweier Zahlen ist das Produkt der Wurzeln:
 . Denn aus der Produktregel beim Quadrieren folgt:
. Denn aus der Produktregel beim Quadrieren folgt:  .
. - Das Gleiche wie für Quadratwurzeln gilt auch für Wurzeln mit höheren Exponenten: Die
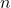 -te Wurzel aus einem Produkt ist das Produkt der
-te Wurzel aus einem Produkt ist das Produkt der 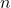 -ten Wurzeln:
-ten Wurzeln: ![Rendered by QuickLaTeX.com \sqrt[n]{a\cdot b} = \sqrt[n]{a} \cdot \sqrt[n]{b}](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-13cfa6786f3f6b0af5496f86e19acadf_l3.png) .
. - Die Wurzel aus einem Bruch ist der Bruch der Wurzeln: Für Zahlen
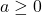 und
und  ist
ist 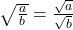 .
. - Das Gleiche wie für Quadratwurzeln von Quotienten und Brüchen gilt auch für Wurzeln mit höheren Exponenten:
![Rendered by QuickLaTeX.com \sqrt[n]{a : b} = \sqrt[n]{a} : \sqrt[n]{b}](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-b47cdd1ccca93ad95bf2c4184b190d17_l3.png) und
und ![Rendered by QuickLaTeX.com \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-c0f44119d67ad07103554fbcd373baf2_l3.png)
Wurzeln aus Summen und Differenzen
- Für Wurzeln aus Summen oder Differenzen gibt es keine Berechnungsformel.
- Die Wurzel aus der Summe zweier Zahlen
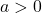 und
und 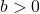 ist nie das Gleiche wie die Summe der Wurzeln dieser Zahlen:
ist nie das Gleiche wie die Summe der Wurzeln dieser Zahlen: 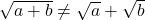 . Denn wenn du die Summe der Wurzeln quadrierst, musst du zur Berechnung die erste binomische Formel verwenden:
. Denn wenn du die Summe der Wurzeln quadrierst, musst du zur Berechnung die erste binomische Formel verwenden:

- Auch für die Summe oder Differenz von Wurzeln gibt es keine Berechnungsformel.
- Die Wurzel aus der Differenz zweier verschiedener Zahlen
 und
und 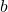 ist nie das Gleiche wie die Summe der Wurzeln dieser Zahlen: Sind
ist nie das Gleiche wie die Summe der Wurzeln dieser Zahlen: Sind 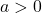 und
und 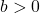 mit
mit  , ist
, ist 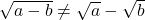 . Denn wenn du die Differenz
. Denn wenn du die Differenz 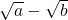 quadrierst, musst du zur Berechnung die zweite binomische Formel benutzen und erhältst:
quadrierst, musst du zur Berechnung die zweite binomische Formel benutzen und erhältst:

Wurzeln aus Potenzen und Potenzen von Wurzeln
- Die Potenz der Wurzel einer Zahl
 ist das Gleiche wie die Wurzel der Potenz dieser Zahl:
ist das Gleiche wie die Wurzel der Potenz dieser Zahl: 
- Umgekehrt ist auch die Wurzel aus der Potenz einer Zahl
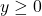 das Gleiche wie die Potenz der Wurzel dieser Zahl:
das Gleiche wie die Potenz der Wurzel dieser Zahl:

- Für eine Zahl
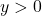 sind die
sind die 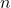 -te Potenz und die
-te Potenz und die 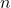 -te Wurzel Operationen, die sich gegenseitig aufheben:
-te Wurzel Operationen, die sich gegenseitig aufheben: ![Rendered by QuickLaTeX.com \sqrt[n]{y^n} = (\sqrt[n]{y})^n =y](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-de1b6494c83ded5392675a78c998cff9_l3.png)
- Die
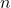 -te Wurzel einer Zahl
-te Wurzel einer Zahl 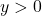 kannst du als Potenz mit dem Exponenten
kannst du als Potenz mit dem Exponenten 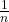 schreiben:
schreiben: ![Rendered by QuickLaTeX.com \sqrt[n]{y}=y^{\frac{1}{n}}](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-7c491b2c075795feee9cb3915dc00df8_l3.png)
- Potenzierst du die
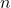 -te Wurzel einer Zahl
-te Wurzel einer Zahl 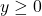 mit dem Exponenten
mit dem Exponenten 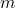 , erhältst du das Gleiche, wie wenn du zuerst potenziert und dann die Wurzel ziehst:
, erhältst du das Gleiche, wie wenn du zuerst potenziert und dann die Wurzel ziehst:
![Rendered by QuickLaTeX.com \big(\sqrt[n]{y}\big)^m = \sqrt[n]{y^m}](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-0a74c7e914e56d95d59e468da2bacf44_l3.png)
Beide Seiten dieser Gleichung kannst du in der Exponentialschreibweise als darstellen.
darstellen.
Übersicht – Wurzelgesetze und Rechenregeln
In der folgenden Tabelle findest du die wichtigsten Formeln zum Wurzelziehen im Überblick:
| Bezeichnung/Rechenoperation | Bedingung/Formel |
|---|---|
| Quadratwurzeln | |
| Radikand |
|
| Wurzelwert |
|
| Exponentialschreibweise | |
| Quadrat | |
| Produkt | |
| Bruch | |
| Summe | |
| Differenz | |
| Potenz | |
| Wurzeln mit Wurzelexponent |
|
| Radikand |
|
| Wurzelwert |
![Rendered by QuickLaTeX.com x=\sqrt[n]{y} \begin{cases} \geq 0\text{, falls }n\text{ gerade} \\ \geq 0\text{, falls }y \geq 0\text{ und }n\text{ ungerade} \\ < 0\text{, falls }y < 0\text{ und }n\text{ ungerade} \end{cases}](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-47e3336bdc3653846b9dcc49c87aa7ca_l3.png) |
| Exponentialschreibweise | |
| Produkt | |
| Bruch | |
| Potenz | |
Wurzeln in der Mathematik – Beispiele und Anwendungen
In der Mathematik gibt es viele verschiedene Situationen, in denen Wurzeln verwendet werden. Wir zeigen dir hier einige typische Beispiele und Anwendungen.
Wurzelterme mit Zahlen und Variablen
Genauso wie aus Zahlen kannst du auch aus Termen mit Variablen Wurzeln ziehen. Dabei musst du die Rechenregeln und Wurzelgesetze berücksichtigen.
Aus einem Term mit Zahlen und Variablen kannst du die Wurzel ziehen, indem du alle Faktoren eines Produkts einzeln berechnest. Dabei musst du auch berücksichtigen, welche Zahlen du für die Variablen einsetzen darfst. Sind beispielsweise ![]() und
und ![]() Variablen, für die nur positive Werte oder
Variablen, für die nur positive Werte oder ![]() eingesetzt werden, ist
eingesetzt werden, ist
![]()
Sind für die Variable ![]() auch negative Werte zulässig, ist
auch negative Werte zulässig, ist
![]()
Negative Werte für die Variable ![]() sind in jedem Fall unzulässig, denn die Quadratwurzeln aus negativen Zahlen sind nicht definiert.
sind in jedem Fall unzulässig, denn die Quadratwurzeln aus negativen Zahlen sind nicht definiert.
Manchmal ist es für Umformungen praktisch, das Wurzelziehen umzukehren, also Terme unter eine Wurzel zu bringen, die außerhalb der Wurzel stehen. Bei Wurzeln mit geraden Exponenten musst du dabei die Vorzeichen beachten. Im Term ![]() kannst du die Variable
kannst du die Variable ![]() unter die Wurzel bringen, indem du sie quadrierst. Dabei musst du aber unbedingt das Vorzeichen von
unter die Wurzel bringen, indem du sie quadrierst. Dabei musst du aber unbedingt das Vorzeichen von ![]() berücksichtigen: Ist
berücksichtigen: Ist ![]() , ist
, ist ![]() . Ist aber
. Ist aber ![]() , ist
, ist ![]() .
.
Genauso wie Quadratwurzeln kannst du auch höhere Wurzeln mit Zahlen und Variablen berechnen. Du kannst Wurzeln ziehen und dadurch Wurzelterme vereinfachen:
![]()
Oder du kannst Variablen unter die Wurzel bringen, indem du sie mit dem Wurzelexponenten potenzierst:
![]()
Oft wird die Berechnung von Wurzeltermen mit Variablen einfacher, wenn du die Exponentialschreibweise verwendest. Wir schreiben im Folgenden also ![]() für die Quadratwurzel aus
für die Quadratwurzel aus ![]() und
und ![]() für die
für die ![]() -te Wurzel aus
-te Wurzel aus ![]() . In dieser Schreibweise ist z. B.
. In dieser Schreibweise ist z. B. ![]() .
.
Nun können wir Wurzelausdrücke mit den Potenzgesetzen umrechnen. Das bedeutet, wir benutzen die Formeln ![]() und
und ![]() zum Umformen von Wurzelausdrücken mit Variablen.
zum Umformen von Wurzelausdrücken mit Variablen.
Beispielsweise lässt sich der komplizierte Ausdruck ![]() mit der Exponentialschreibweise und dem Potenzgesetz zu
mit der Exponentialschreibweise und dem Potenzgesetz zu ![]() vereinfachen:
vereinfachen:
![]()
Analog kannst du den Term ![]() mit dem Potenzgesetz zu
mit dem Potenzgesetz zu ![]() vereinfachen:
vereinfachen:
![]()
Wurzeln ziehen mit Zahlen und Einheiten
Du kennst schon Rechnungen mit Einheiten und Potenzen: Den Flächeninhalt eines Rechtecks misst du in Einheiten wie ![]() oder
oder ![]() oder
oder ![]() usw. Den Rauminhalt eines Gefäßes oder eines Raums misst du in Einheiten wie
usw. Den Rauminhalt eines Gefäßes oder eines Raums misst du in Einheiten wie ![]() oder
oder ![]() oder
oder ![]() . Wenn du mit solchen Einheiten rechnest, kann es vorkommen, dass du auch Wurzeln ziehen musst. Hier sind zwei Beispiele:
. Wenn du mit solchen Einheiten rechnest, kann es vorkommen, dass du auch Wurzeln ziehen musst. Hier sind zwei Beispiele:
Gegeben ist ein Rechteck mit den Kantenlängen ![]() und
und ![]() . Welche Kantenlänge hat ein Quadrat mit dem gleichen Flächeninhalt wie das Rechteck? Um die Aufgabe zu lösen, berechnen wir zuerst den Flächeninhalt des Rechtecks mit der Formel
. Welche Kantenlänge hat ein Quadrat mit dem gleichen Flächeninhalt wie das Rechteck? Um die Aufgabe zu lösen, berechnen wir zuerst den Flächeninhalt des Rechtecks mit der Formel ![]() . Für
. Für ![]() und
und ![]() setzen wir die gegebenen Kantenlängen ein und erhalten:
setzen wir die gegebenen Kantenlängen ein und erhalten:
![]()
Den Flächeninhalt eines Quadrats mit Kantenlänge ![]() berechnen wir mit der Formel
berechnen wir mit der Formel ![]() . Wir setzen also
. Wir setzen also ![]() . Um die Kantenlänge
. Um die Kantenlänge ![]() zu berechnen, ziehen wir die Wurzel aus
zu berechnen, ziehen wir die Wurzel aus ![]() :
:
![]()
Die Kantenlänge des gesuchten Quadrats beträgt also ![]() .
.
Im zweiten Beispiel betrachten wir den Rauminhalt. Ein Liter ist das Gleiche wie ein Kubikdezimeter: ![]() . Mit anderen Worten: Ein Liter Wasser passt genau in einen Würfel der Kantenlänge
. Mit anderen Worten: Ein Liter Wasser passt genau in einen Würfel der Kantenlänge ![]() . Wie groß muss ein würfelförmiges Gefäß dann sein, damit
. Wie groß muss ein würfelförmiges Gefäß dann sein, damit ![]() Wasser hineinpassen? Es muss natürlich doppelt so groß sein, wenn man den Rauminhalt misst, denn es sollen ja
Wasser hineinpassen? Es muss natürlich doppelt so groß sein, wenn man den Rauminhalt misst, denn es sollen ja ![]() Wasser hineinpassen. Aber wie lang müssen die Seiten des Würfels sein? Um das zu berechnen, verwenden wir die Formel für das Volumen
Wasser hineinpassen. Aber wie lang müssen die Seiten des Würfels sein? Um das zu berechnen, verwenden wir die Formel für das Volumen ![]() eines Würfels:
eines Würfels: ![]() . Dabei ist
. Dabei ist ![]() die Kantenlänge des Würfels. Wir setzen den bekannten Rauminhalt ein:
die Kantenlänge des Würfels. Wir setzen den bekannten Rauminhalt ein: ![]() . Um die Gleichung
. Um die Gleichung ![]() nach der unbekannten Kantenlänge
nach der unbekannten Kantenlänge ![]() aufzulösen, ziehen wir die dritte Wurzel:
aufzulösen, ziehen wir die dritte Wurzel:
![]()
Der Würfel muss also eine Kantenlänge von ca. ![]() haben, damit sein Rauminhalt
haben, damit sein Rauminhalt ![]() beträgt. Die Lösung
beträgt. Die Lösung ![]() ist nur eine Approximation der dritten Wurzel. Tatsächlich ist
ist nur eine Approximation der dritten Wurzel. Tatsächlich ist ![]() eine irrationale Zahl, also eine nicht periodische Dezimalzahl mit unendlich vielen Stellen. Das Problem der Würfelverdoppelung ist also nicht durch eine Bruchzahl lösbar.
eine irrationale Zahl, also eine nicht periodische Dezimalzahl mit unendlich vielen Stellen. Das Problem der Würfelverdoppelung ist also nicht durch eine Bruchzahl lösbar.
Wurzeln und der Satz des Pythagoras
In einem rechtwinkligen Dreieck gilt für die Längen der drei Seiten der Satz des Pythagoras: Die Summe der Quadrate der beiden kürzeren Seiten – also der Katheten – ist gleich dem Quadrat der längsten Seite – also der Hypotenuse.
Meistens werden die Seiten in einem rechtwinkligen Dreieck mit den Buchstaben ![]() ,
, ![]() und
und ![]() bezeichnet, wobei
bezeichnet, wobei ![]() für die Hypotenuse steht.
für die Hypotenuse steht.
In diesem Fall kannst du den Satz des Pythagoras durch die Formel ![]() ausdrücken.
ausdrücken.
Der Satz des Pythagoras und das Wurzelziehen werden verwendet, um die Länge einer Seite im rechtwinkligen Dreieck zu berechnen, wenn nur die beiden anderen Seitenlängen bekannt sind. Wir betrachten zuerst ein rechtwinkliges Dreieck mit den beiden Katheten ![]() und
und ![]() . Gesucht ist die Länge der Hypotenuse
. Gesucht ist die Länge der Hypotenuse ![]() . Mit dem Satz des Pythagoras erhalten wir:
. Mit dem Satz des Pythagoras erhalten wir:
![]()
Die Länge ![]() erhalten wir, indem wir aus
erhalten wir, indem wir aus ![]() die Wurzel ziehen:
die Wurzel ziehen:
![]()
Ganz analog können wir auch die Länge einer der Katheten berechnen, wenn die Längen der anderen Kathete und der Hypotenuse bekannt sind. Wir betrachten ein rechtwinkliges Dreieck mit den Seitenlängen ![]() und
und ![]() . Die Formel
. Die Formel ![]() lösen wir zuerst nach
lösen wir zuerst nach ![]() auf, da
auf, da ![]() die unbekannte Länge ist:
die unbekannte Länge ist:
![]()
Indem wir aus dem Term ![]() die Wurzel ziehen, erhalten wir die gesuchte Länge:
die Wurzel ziehen, erhalten wir die gesuchte Länge:
![]()
Wurzeln zum Lösen quadratischer Gleichungen
Steht eine Variable zum Quadrat in einer Gleichung, musst du eine Wurzel ziehen, um die Gleichung zu lösen. Bei einer quadratischen Gleichung in allgemeiner Form ![]() oder in Normalform
oder in Normalform ![]() geht das Wurzelziehen aber nicht direkt. Denn aus einer Summe kannst du nicht die Wurzel ziehen. Du musst die Gleichung erst zu einem Quadrat umformen, aus dem du dann die Wurzel ziehen kannst. Das Verfahren der Umformung nennt man quadratische Ergänzung.
geht das Wurzelziehen aber nicht direkt. Denn aus einer Summe kannst du nicht die Wurzel ziehen. Du musst die Gleichung erst zu einem Quadrat umformen, aus dem du dann die Wurzel ziehen kannst. Das Verfahren der Umformung nennt man quadratische Ergänzung.
Bei einer Gleichung in Normalform erhältst du durch die quadratische Ergänzung die äquivalente Gleichung ![]() . Nun kannst du aus beiden Seiten der Gleichung die Wurzel ziehen und erhältst die Gleichung
. Nun kannst du aus beiden Seiten der Gleichung die Wurzel ziehen und erhältst die Gleichung ![]() . Da auch die Gegenzahl der Wurzel die Gleichung löst, erhältst du für die zweite Lösung der quadratischen Gleichung die Darstellung
. Da auch die Gegenzahl der Wurzel die Gleichung löst, erhältst du für die zweite Lösung der quadratischen Gleichung die Darstellung ![]() . Beide Lösungen werden in der
. Beide Lösungen werden in der ![]() -Formel zusammengefasst:
-Formel zusammengefasst:
![]()
Eine quadratische Gleichung in allgemeiner Form kannst du in ähnlicher Weise quadratisch ergänzen, sodass eine Wurzel zu der Lösung führt. Die Lösungsformel, die du dadurch erhältst, ist die Mitternachtsformel:
![]()
Wurzeln in der höheren Mathematik
Mit Wurzeln kann man in der Mathematik noch eine Menge mehr machen, als wir hier erklären können. Wir zeigen nur zwei kleine Ausblicke, in denen die Mathematik des Wurzelziehens komplizierter und komplexer wird.
Die Wurzelfunktionen
Für jede nicht negative Zahl ![]() haben wir oben die Wurzel
haben wir oben die Wurzel ![]() definiert. Tragen wir in einem Koordinatensystem über jedem
definiert. Tragen wir in einem Koordinatensystem über jedem ![]() in der
in der ![]() -Richtung den Wurzelwert
-Richtung den Wurzelwert ![]() ab, erhalten wir den Funktionsgraphen der Wurzelfunktion
ab, erhalten wir den Funktionsgraphen der Wurzelfunktion ![]() .
.
Das Gleiche können wir auch für Wurzeln mit höheren Wurzelexponenten machen und erhalten die Funktionsgraphen der Funktionen ![]() . Auf diese Weise erhältst du für jeden Wurzelexponenten
. Auf diese Weise erhältst du für jeden Wurzelexponenten ![]() eine Wurzelfunktion. Alle diese Wurzelfunktionen haben zwei Werte gemeinsam: Für jedes
eine Wurzelfunktion. Alle diese Wurzelfunktionen haben zwei Werte gemeinsam: Für jedes ![]() ist
ist ![]() und
und ![]() .
.
Bei der Definition der Wurzelfunktionen musst du beachten, dass der Definitions- und der Wertebereich der Funktion ![]() vom Wurzelexponenten abhängen: Ist
vom Wurzelexponenten abhängen: Ist ![]() gerade, ist der Definitions- und Wertebereich von
gerade, ist der Definitions- und Wertebereich von ![]() jeweils der Bereich
jeweils der Bereich ![]() der nicht negativen reellen Zahlen. In dem folgenden Diagramm siehst du die Funktionsgraphen solcher Wurzelfunktionen für verschiedene Wurzelexponenten
der nicht negativen reellen Zahlen. In dem folgenden Diagramm siehst du die Funktionsgraphen solcher Wurzelfunktionen für verschiedene Wurzelexponenten ![]() .
.
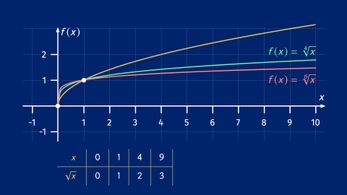
Ist ![]() ungerade, ist der Definitions- und Wertebereich der Wurzelfunktion
ungerade, ist der Definitions- und Wertebereich der Wurzelfunktion ![]() jeweils
jeweils ![]() . Diese Wurzelfunktionen haben einen weiteren gemeinsamen Wert: Für jedes ungerade
. Diese Wurzelfunktionen haben einen weiteren gemeinsamen Wert: Für jedes ungerade ![]() ist
ist ![]() . In dem folgenden Diagramm sind Funktionsgraphen von Wurzelfunktionen
. In dem folgenden Diagramm sind Funktionsgraphen von Wurzelfunktionen ![]() für drei verschiedene, ungerade Werte von
für drei verschiedene, ungerade Werte von ![]() eingezeichnet. Du erkennst deutlich die gemeinsamen Punkte
eingezeichnet. Du erkennst deutlich die gemeinsamen Punkte ![]() und
und ![]() und
und ![]() .
.
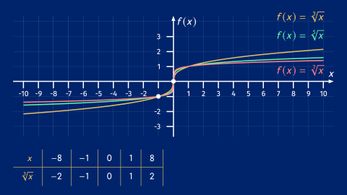
Quadratwurzeln aus negativen Zahlen
Die Wurzel aus einer Zahl ![]() ist eine Lösung
ist eine Lösung ![]() der Gleichung
der Gleichung ![]() . Ist
. Ist ![]() , gibt es keine reelle Zahl
, gibt es keine reelle Zahl ![]() , die die Gleichung
, die die Gleichung ![]() löst. Denn für jede reelle Zahl
löst. Denn für jede reelle Zahl ![]() ist
ist ![]() . Da die Gleichung
. Da die Gleichung ![]() für
für ![]() nicht lösbar ist, ist das Wurzelziehen in den reellen Zahlen nicht möglich, wenn der Radikand negativ ist.
nicht lösbar ist, ist das Wurzelziehen in den reellen Zahlen nicht möglich, wenn der Radikand negativ ist.
Dass eine Gleichung in einem bestimmten Zahlenbereich nicht lösbar ist, kennst du bestimmt schon: Die Gleichung ![]() ist nicht lösbar, solange du nur mit natürlichen Zahlen rechnest. Durch die Zahlbereichserweiterung zu den ganzen Zahlen wird die Gleichung
ist nicht lösbar, solange du nur mit natürlichen Zahlen rechnest. Durch die Zahlbereichserweiterung zu den ganzen Zahlen wird die Gleichung ![]() lösbar durch
lösbar durch ![]() . Im Zahlbereich
. Im Zahlbereich ![]() der ganzen Zahlen ist dann jede additive Gleichung, in der ganze Zahlen vorkommen, auch durch ganze Zahlen lösbar. Ganz analog ist die Gleichung
der ganzen Zahlen ist dann jede additive Gleichung, in der ganze Zahlen vorkommen, auch durch ganze Zahlen lösbar. Ganz analog ist die Gleichung ![]() nicht lösbar, solange du nur mit ganzen Zahlen rechnest. Erst durch die Erweiterung zu den rationalen Zahlen wird die Gleichung
nicht lösbar, solange du nur mit ganzen Zahlen rechnest. Erst durch die Erweiterung zu den rationalen Zahlen wird die Gleichung ![]() lösbar durch
lösbar durch ![]() . Im Zahlbereich
. Im Zahlbereich ![]() der rationalen Zahlen ist dann auch jede multiplikative Gleichung, in der rationale Zahlen vorkommen, mit rationalen Zahlen lösbar.
der rationalen Zahlen ist dann auch jede multiplikative Gleichung, in der rationale Zahlen vorkommen, mit rationalen Zahlen lösbar.
Im Zahlbereich ![]() ist aber nicht jede polynomiale Gleichung lösbar. Denn die Gleichung
ist aber nicht jede polynomiale Gleichung lösbar. Denn die Gleichung ![]() hat die Lösungen
hat die Lösungen ![]() und
und ![]() . Diese Lösungen sind keine rationalen Zahlen, sondern reelle Zahlen. Um polynomiale Gleichungen mit rationalen Koeffizienten zu lösen, ist also die Erweiterung zu einem Zahlbereich nötig, der auch reelle Zahlen enthält. Das genügt aber nicht, um jede solche Gleichung zu lösen, denn die Gleichung
. Diese Lösungen sind keine rationalen Zahlen, sondern reelle Zahlen. Um polynomiale Gleichungen mit rationalen Koeffizienten zu lösen, ist also die Erweiterung zu einem Zahlbereich nötig, der auch reelle Zahlen enthält. Das genügt aber nicht, um jede solche Gleichung zu lösen, denn die Gleichung ![]() hat keine reelle Zahl als Lösung. Außerdem enthält der Zahlbereich
hat keine reelle Zahl als Lösung. Außerdem enthält der Zahlbereich ![]() der reellen Zahlen auch Zahlen, die gar keine Lösungen solcher Gleichungen sind, z. B.
der reellen Zahlen auch Zahlen, die gar keine Lösungen solcher Gleichungen sind, z. B. ![]() oder
oder ![]() .
.
Es ist möglich, den Zahlbereich ![]() der reellen Zahlen so zu erweitern, dass auch Wurzeln negativer Zahlen existieren. Zahlen in dieser Erweiterung nennt man komplexe Zahlen. Um die Menge aller komplexen Zahlen zu definieren, führt man zuerst das Symbol
der reellen Zahlen so zu erweitern, dass auch Wurzeln negativer Zahlen existieren. Zahlen in dieser Erweiterung nennt man komplexe Zahlen. Um die Menge aller komplexen Zahlen zu definieren, führt man zuerst das Symbol ![]() ein und definiert
ein und definiert ![]() . Indem man dieses
. Indem man dieses ![]() mit beliebigen reellen Zahlen kombiniert, erhält man Zahlen der Form
mit beliebigen reellen Zahlen kombiniert, erhält man Zahlen der Form ![]() mit
mit ![]() . Zahlen
. Zahlen ![]() dieser Form heißen komplexe Zahlen. Die Zahl
dieser Form heißen komplexe Zahlen. Die Zahl ![]() nennt man die imaginäre Einheit. Die reellen Zahlen
nennt man die imaginäre Einheit. Die reellen Zahlen ![]() und
und ![]() in der Darstellung
in der Darstellung ![]() heißen Realteil von
heißen Realteil von ![]() und Imaginärteil von
und Imaginärteil von ![]() . Den Zahlbereich aller komplexen Zahlen bezeichnet man mit dem Symbol
. Den Zahlbereich aller komplexen Zahlen bezeichnet man mit dem Symbol ![]() . Das Symbol
. Das Symbol ![]() steht übrigens für imaginär. Denn Zahlen, deren Quadrat negativ ist, galten lange als bloß vorgestellte (imaginäre) und nicht wirkliche (reelle) Zahlen.
steht übrigens für imaginär. Denn Zahlen, deren Quadrat negativ ist, galten lange als bloß vorgestellte (imaginäre) und nicht wirkliche (reelle) Zahlen.
Mit komplexen Zahlen ![]() kann man dann ganz genauso rechnen wie mit reellen Zahlen. Beim Multiplizieren muss man nur die Gleichung
kann man dann ganz genauso rechnen wie mit reellen Zahlen. Beim Multiplizieren muss man nur die Gleichung ![]() berücksichtigen.
berücksichtigen.
Häufig gestellte Fragen zum Thema Wurzel ziehen
