Obersumme und Untersumme – Berechnung von Integralen
Erfahre, wie du mithilfe von Obersumme und Untersumme den Flächeninhalt unter einem Funktionsgraphen annähern kannst. Entdecke die Bedeutung von Teilintervallen und Feinheit und wie diese zur Berechnung beitragen. Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Obersumme und Untersumme
Obersumme und Untersumme – Erklärung & Definition
Die Obersumme und Untersumme dienen dazu, für eine gegebene Funktion über ein Intervall ![]() den Flächeninhalt zwischen dem Funktionsgraphen und der
den Flächeninhalt zwischen dem Funktionsgraphen und der ![]() -Achse näherungsweise zu berechnen. Dafür unterteilst du dieses Intervall in
-Achse näherungsweise zu berechnen. Dafür unterteilst du dieses Intervall in ![]() Teilintervalle derselben Länge
Teilintervalle derselben Länge ![]() . Die Länge der Teilintervalle wird auch Feinheit genannt. Anstelle des Flächeninhalts der Fläche, die von dem Funktionsgraphen und der
. Die Länge der Teilintervalle wird auch Feinheit genannt. Anstelle des Flächeninhalts der Fläche, die von dem Funktionsgraphen und der ![]() -Achse begrenzt wird, berechnest du die Fläche von Rechtecken.
-Achse begrenzt wird, berechnest du die Fläche von Rechtecken.
Die Teilintervalle stellen die Länge der Grundseite der Rechtecke dar. Die Höhe eines Rechtecks über einem Teilintervall ist der jeweils größte bzw. kleinste Funktionswert in diesem Teilintervall.
Formel der Obersumme
Bei der Obersumme ![]() wird der im Teilintervall größte Funktionswert betrachtet. Die Anzahl der Teilintervalle ist
wird der im Teilintervall größte Funktionswert betrachtet. Die Anzahl der Teilintervalle ist ![]() .
.
Die Formel für die Obersumme der Funktion ![]() über dem Intervall
über dem Intervall ![]() lautet:
lautet:
![]()
Die Obersumme wird auch mit ![]() bezeichnet.
bezeichnet.
Formel der Untersumme
Für die Berechnung der Untersumme ![]() ist der kleinste Funktionswert im Teilintervall relevant.
ist der kleinste Funktionswert im Teilintervall relevant.
Du berechnest sie mit der Formel:
![Rendered by QuickLaTeX.com \displaystyle U(n)= \sum\limits_{i=0}^{n-1} \text{min}_{x \in [x_i,x_{i+1}]}(f(x)) \cdot \Delta x](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-c6fe04d1b35a0662b0b615eaa7f77f49_l3.png)
Die Untersumme wird auch mit ![]() bezeichnet.
bezeichnet.
Integralrechnung und Herleitung mit der Obersumme und Untersumme – Streifenmethode
Obersumme und Untersumme können die Fläche unter einem Funktionsgraphen annähern.
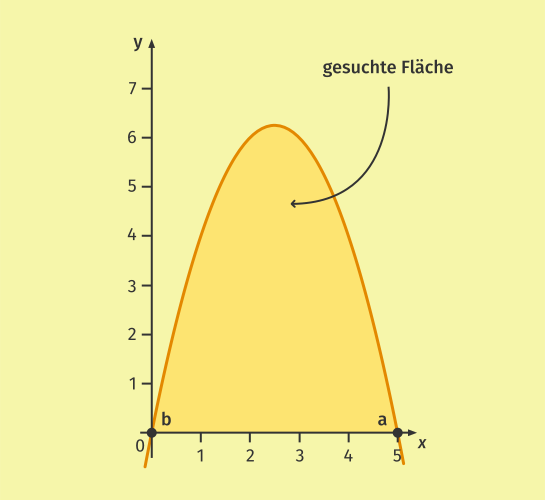
Betrachte beispielhaft die nachfolgende Parabel.
Diese schließt gemeinsam mit der ![]() -Achse eine Fläche
-Achse eine Fläche ![]() ein.
ein.
Um diese Fläche zu berechnen bzw. diese anzunähern, kannst du die Obersumme oder die Untersumme bilden.
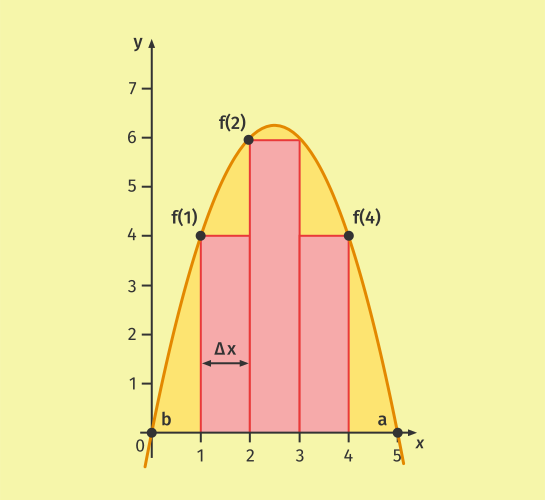
In der folgenden Abbildung wurde für die Untersumme eine Feinheit von ![]() gewählt.
gewählt.
Die kleinsten Funktionswerte in den Teilintervallen sind
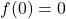 im Teilintervall
im Teilintervall ![Rendered by QuickLaTeX.com [0;1]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-41a47ffea3279fce6748330a2744c289_l3.png)
 im Teilintervall
im Teilintervall ![Rendered by QuickLaTeX.com [1;2]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-1d5351b8309b53dd9eba802da876388f_l3.png)
 im Teilintervall
im Teilintervall ![Rendered by QuickLaTeX.com [2;3]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-888a255f59f1e86a85d83eab0d86ce4a_l3.png)
 im Teilintervall
im Teilintervall ![Rendered by QuickLaTeX.com [3;4]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-cb6c2c48aaa66db5172c72b5d8496a1c_l3.png)
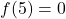 im Teilintervall
im Teilintervall ![Rendered by QuickLaTeX.com [4;5]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-4334e534c167ed9be229e63547030017_l3.png)
Die Untersumme der Funktion mit der gewählten Feinheit ![]() ist:
ist:
![]()
Es ist zu erkennen, dass die Summe der Flächeninhalte der Rechtecke kleiner ist als die gesuchte Fläche ![]() . Es gilt also:
. Es gilt also:
![]()
Die Obersumme über demselben Intervall ist in der nächsten Abbildung dargestellt. Auch hier wurde eine Feinheit von ![]() gewählt.
gewählt.
Die größten Funktionswerte in den Teilintervallen sind
 im Teilintervall
im Teilintervall ![Rendered by QuickLaTeX.com [0;1]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-41a47ffea3279fce6748330a2744c289_l3.png)
 im Teilintervall
im Teilintervall ![Rendered by QuickLaTeX.com [1;2]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-1d5351b8309b53dd9eba802da876388f_l3.png)
 im Teilintervall
im Teilintervall ![Rendered by QuickLaTeX.com [2;3]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-888a255f59f1e86a85d83eab0d86ce4a_l3.png)
 im Teilintervall
im Teilintervall ![Rendered by QuickLaTeX.com [3;4]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-cb6c2c48aaa66db5172c72b5d8496a1c_l3.png)
 im Teilintervall
im Teilintervall ![Rendered by QuickLaTeX.com [4;5]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-4334e534c167ed9be229e63547030017_l3.png)
Die Obersumme der Funktion berechnet sich mit:
![]()
In diesem Fall ist die Summe der Flächeninhalte der Rechtecke größer als der gesuchte Flächeninhalt.
![]()
Insgesamt gilt also ![]() .
.
Damit sich Ober- bzw. Untersumme an den gesuchten Flächeninhalt annähern, bildest du den Grenzwert ![]() der Ober- bzw. Untersumme.
der Ober- bzw. Untersumme.
Das bedeutet, dass die Feinheit der Teilintervalle immer kleiner wird.
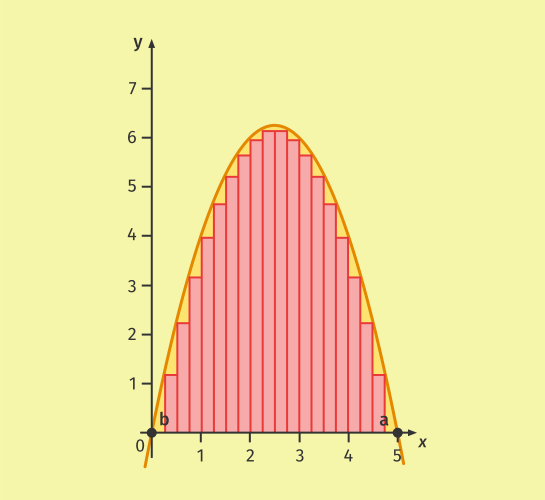
Wie du in folgender Abbildung sehen kannst, nähert sich die Untersumme so dem Flächeninhalt ![]() immer weiter an.
immer weiter an.
Im Grenzwert ![]() werden Obersumme und Untersumme gleich. Es gilt also:
werden Obersumme und Untersumme gleich. Es gilt also:
![]()
Obersumme und Untersumme nehmen also im Grenzwert den gleichen Wert an und beschreiben so den gesuchten Flächeninhalt. Man spricht auch von dem bestimmten Integral der Funktion.
Diese Methode der Annäherung an das bestimmte Integral einer Funktion durch Obersumme und Untersumme wird auch als Streifenmethode des Archimedes bezeichnet.
Obersumme und Untersumme – Beispiel
Um annähernd zu berechnen, wie groß die Fläche ![]() zwischen dem Funktionsgraphen von
zwischen dem Funktionsgraphen von ![]() und der
und der ![]() -Achse ist, kannst du die Untersumme im Intervall
-Achse ist, kannst du die Untersumme im Intervall ![]() berechnen.
berechnen.
Wähle die Feinheit ![]() , wodurch sich vier Teilintervalle ergeben.
, wodurch sich vier Teilintervalle ergeben.
Die kleinsten Funktionswerte sind
 im Intervall
im Intervall ![Rendered by QuickLaTeX.com [0;1]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-41a47ffea3279fce6748330a2744c289_l3.png)
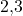 im Intervall
im Intervall ![Rendered by QuickLaTeX.com [1;2]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-1d5351b8309b53dd9eba802da876388f_l3.png)
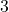 im Intervall
im Intervall ![Rendered by QuickLaTeX.com [2;3]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-888a255f59f1e86a85d83eab0d86ce4a_l3.png)
 im Intervall
im Intervall ![Rendered by QuickLaTeX.com [3;4]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-cb6c2c48aaa66db5172c72b5d8496a1c_l3.png)
Dann ist die gesuchte Untersumme ![]() .
.

Häufig gestellte Fragen zum Thema Obersumme und Untersumme