Nullstellen berechnen – Definition, Verfahren und Anwendungen
Erfahre, was Nullstellen sind und wie sie den Funktionsgraphen beeinflussen. Entdecke die verschiedenen Typen von Funktionen, ihre Nullstellen und Lösungsverfahren wie pq-Formel, Polynomdivision und mehr. Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Nullstellen berechnen
Nullstellen von Funktionen – Definition und Eigenschaften
In diesem Text wird das Berechnen von Nullstellen verschiedener Funktionen einfach erklärt. Wir zeigen zuerst, was Nullstellen sind und wie du die Nullstellen am Funktionsgraphen erkennst. Danach schauen wir uns verschiedene Funktionstypen an und erklären, unter welchen Voraussetzungen sie Nullstellen besitzen – und wenn ja, wie viele. Schließlich erklären wir verschiedene Verfahren, um Nullstellen zu berechnen, und erläutern sie an Beispielen.
Nullstellen – Definition und Bedeutung
Eine Nullstelle einer Funktion ![]() ist ein
ist ein ![]() -Wert, für den der Funktionswert null ist. Mit anderen Worten: Setzt man diesen
-Wert, für den der Funktionswert null ist. Mit anderen Worten: Setzt man diesen ![]() -Wert in den Funktionsterm ein, kommt
-Wert in den Funktionsterm ein, kommt ![]() heraus. Nullstellen sind also nicht beliebige oder variable
heraus. Nullstellen sind also nicht beliebige oder variable ![]() -Werte, sondern ganz bestimmte
-Werte, sondern ganz bestimmte ![]() -Werte. Verschiedene Funktionen haben im Allgemeinen verschiedene Nullstellen.
-Werte. Verschiedene Funktionen haben im Allgemeinen verschiedene Nullstellen.
Weil Funktionen oft mehrere Nullstellen haben, ist es praktisch, die Nullstellen zu nummerieren. Wir schreiben also ![]() ,
, ![]() und
und ![]() usw. für die erste, zweite und dritte Nullstelle.
usw. für die erste, zweite und dritte Nullstelle.
Die Nullstellen einer Funktion zu bestimmen, bedeutet, die Gleichung ![]() zu lösen. Ob die Gleichung lösbar ist und wie du die Lösungen der Gleichung bestimmst, hängt stark von der Funktion
zu lösen. Ob die Gleichung lösbar ist und wie du die Lösungen der Gleichung bestimmst, hängt stark von der Funktion ![]() ab. Lösungsmethoden für verschiedene Funktionstypen schauen wir uns im nächsten Abschnitt an.
ab. Lösungsmethoden für verschiedene Funktionstypen schauen wir uns im nächsten Abschnitt an.
Was es bedeutet, dass ![]() eine Nullstellen der Funktion
eine Nullstellen der Funktion ![]() sind, kannst du dir am Funktionsgraphen veranschaulichen: Punkte auf dem Funktionsgraphen haben die Form
sind, kannst du dir am Funktionsgraphen veranschaulichen: Punkte auf dem Funktionsgraphen haben die Form ![]() . An einer Nullstelle
. An einer Nullstelle ![]() erhält man also den Punkt
erhält man also den Punkt ![]() . Ein Punkt dieser Form liegt auf der
. Ein Punkt dieser Form liegt auf der ![]() -Achse, denn die
-Achse, denn die ![]() -Koordinate des Punkts ist
-Koordinate des Punkts ist ![]() . Wir haben also herausgefunden: Nullstellen einer Funktion sind dasselbe wie die Schnittstellen des Funktionsgraphen mit der
. Wir haben also herausgefunden: Nullstellen einer Funktion sind dasselbe wie die Schnittstellen des Funktionsgraphen mit der ![]() -Achse. Die Nullstellen gehören damit zu den Achsenabschnitten.
-Achse. Die Nullstellen gehören damit zu den Achsenabschnitten.
Beispiele – Nullstellen linearer und quadratischer Funktionen
Wir zeigen in diesem Abschnitt am Beispiel linearer und quadratischer Funktionen, was Nullstellen sind. Verfahren zur Bestimmung von Nullstellen für verschiedene Funktionstypen werden im nächsten Abschnitt erklärt.
Nullstellen linearer Funktionen
Der Funktionsgraph einer linearen Funktion ![]() ist eine Gerade im Koordinatensystem mit Steigung
ist eine Gerade im Koordinatensystem mit Steigung ![]() und
und ![]() -Achsenabschnitt
-Achsenabschnitt ![]() .
.

- Aus dem Funktionsgraphen kannst du die Nullstellen ablesen:
Die lineare Funktion schneidet die
schneidet die  -Achse an der Stelle
-Achse an der Stelle  . Setzt du diesen Wert in den Funktionsterm ein, erhältst du:
. Setzt du diesen Wert in den Funktionsterm ein, erhältst du:  . Die Schnittstelle mit der
. Die Schnittstelle mit der  -Achse ist eine Nullstelle der Funktion.
-Achse ist eine Nullstelle der Funktion. - Umgekehrt kannst du auch die Nullstellengleichung
 nach
nach  auflösen und erhältst
auflösen und erhältst 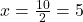 . Die Nullstelle
. Die Nullstelle  der Funktion
der Funktion  ist die Schnittstelle des Funktionsgraphen von
ist die Schnittstelle des Funktionsgraphen von  mit der
mit der  -Achse.
-Achse.
Nullstellen quadratischer Funktionen
Der Funktionsgraph einer quadratischen Funktion ![]() ist eine Parabel im Koordinatensystem, deren Symmetrieachse auf der
ist eine Parabel im Koordinatensystem, deren Symmetrieachse auf der ![]() -Achse liegt oder parallel dazu verläuft. Eine solche Parabel schneidet die
-Achse liegt oder parallel dazu verläuft. Eine solche Parabel schneidet die ![]() -Achse entweder an zwei Stellen
-Achse entweder an zwei Stellen ![]() und
und ![]() oder an einer Stelle
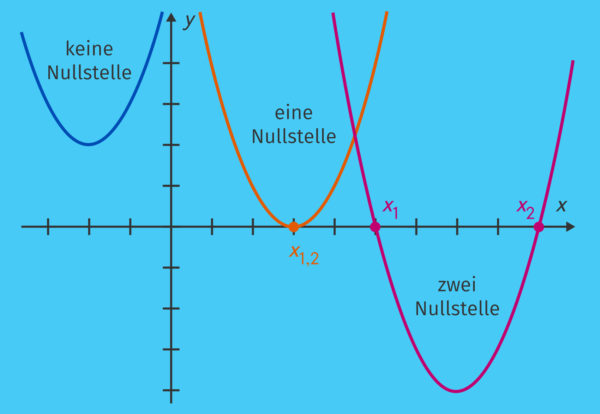
oder an einer Stelle ![]() oder gar nicht. Da die Nullstellen der Funktion dasselbe sind wie die Schnittstellen des Funktionsgraphen mit der
oder gar nicht. Da die Nullstellen der Funktion dasselbe sind wie die Schnittstellen des Funktionsgraphen mit der ![]() -Achse, hat eine quadratische Funktion entweder zwei verschiedene Nullstellen oder eine Nullstelle oder keine Nullstelle.
-Achse, hat eine quadratische Funktion entweder zwei verschiedene Nullstellen oder eine Nullstelle oder keine Nullstelle.
Existenz, Anzahl und Vielfachheit von Nullstellen
Ob eine Funktion Nullstellen hat oder nicht – und wenn ja: wie viele – hängt vom Funktionstyp ab. Die wichtigsten Funktionstypen sind die folgenden.
Nullstellen – lineare Funktionen
- Eine lineare Funktion
 , mit
, mit  , hat genau eine Nullstelle.
, hat genau eine Nullstelle. - Die Nullstelle der Funktion
 ist
ist  .
. - Die Funktion
 hat keine Nullstelle, wenn
hat keine Nullstelle, wenn  ist.
ist. - Die Nullfunktion
 hat unendlich viele Nullstellen.
hat unendlich viele Nullstellen.
Nullstellen – quadratische Funktionen
- Eine quadratische Funktion hat höchstens zwei Nullstellen.
- Die Nullstellen der quadratischen Funktion
 in allgemeiner Form findest du mit der Mitternachtsformel:
in allgemeiner Form findest du mit der Mitternachtsformel:

Ist der Term unter der Wurzel negativ, hat die Funktion
unter der Wurzel negativ, hat die Funktion  keine Nullstellen. Ist der Term
keine Nullstellen. Ist der Term 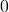 , hat
, hat  eine Nullstelle, die dann doppelte Nullstelle heißt. Ist der Term
eine Nullstelle, die dann doppelte Nullstelle heißt. Ist der Term  positiv, hat
positiv, hat  die beiden verschiedenen Nullstellen
die beiden verschiedenen Nullstellen  und
und  . Der Term
. Der Term  wird als Diskriminante bezeichnet.
wird als Diskriminante bezeichnet. - Die Nullstellen der quadratischen Funktion
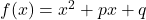 in Normalform findest du mit der pq-Formel:
in Normalform findest du mit der pq-Formel:

Ist der Term unter der Wurzel negativ, hat
unter der Wurzel negativ, hat  keine Nullstelle. Ist dieser Term
keine Nullstelle. Ist dieser Term 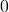 , hat
, hat  nur eine Nullstelle. Sie heißt doppelte Nullstelle. Ist der Term
nur eine Nullstelle. Sie heißt doppelte Nullstelle. Ist der Term  positiv, hat die Funktion
positiv, hat die Funktion  die beiden verschiedenen Nullstellen
die beiden verschiedenen Nullstellen  und
und  .
. - Liegt die quadratische Funktion in faktorisierter Form oder Nullstellenform
 vor, kannst du die Nullstellen
vor, kannst du die Nullstellen  und
und  direkt ablesen. Ist
direkt ablesen. Ist 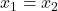 , heißt dieser
, heißt dieser  -Wert doppelte Nullstelle von
-Wert doppelte Nullstelle von  .
.
Nullstellen – ganzrationale Funktionen vom Grad ![]()
- Eine ganzrationale Funktion vom Grad
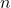 hat höchstens
hat höchstens 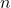 verschiedene Nullstellen. Als ganzrationale Funktion vom Grad
verschiedene Nullstellen. Als ganzrationale Funktion vom Grad 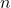 wird eine Polynomfunktion vom Grad
wird eine Polynomfunktion vom Grad 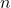 bezeichnet.
bezeichnet. - Funktionen ungeraden Grads – beispielsweise Funktionen dritten Grads – haben mindestens eine Nullstelle.
- Funktionen geraden Grads können auch gar keine Nullstellen haben. Die Funktion
 beispielsweise hat keine Nullstellen, denn die Terme
beispielsweise hat keine Nullstellen, denn die Terme  und
und 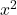 können keine negativen Werte annehmen.
können keine negativen Werte annehmen.
Nullstellen – gebrochen rationale Funktionen
- Die Nullstellen einer gebrochen rationalen Funktion
 mit Polynomfunktionen
mit Polynomfunktionen  und
und  ,
,  , entsprechen den Nullstellen der Funktion im Zähler.
, entsprechen den Nullstellen der Funktion im Zähler.
Denn ein Bruch ist genau dann null, wenn der Zähler null ist.
Zusätzlich musst du die Definitionsmenge der Funktion berücksichtigen, die durch die Funktion im Nenner bestimmt wird. Werte, die nicht Teil der Definitionsmenge sind, können nicht Nullstellen der Funktion sein. - Um die Nullstellen des Bruchs
 zu berechnen, musst du also nur die Nullstellen der Funktion
zu berechnen, musst du also nur die Nullstellen der Funktion  im Zähler berechnen und prüfen, ob diese Teil der Definitionsmenge sind.
im Zähler berechnen und prüfen, ob diese Teil der Definitionsmenge sind.
Nullstellen – Sinus- und Cosinusfunktionen
- Die Sinusfunktion
 hat bei jeder ganzen Zahl
hat bei jeder ganzen Zahl  eine Nullstelle, denn für jede ganze Zahl
eine Nullstelle, denn für jede ganze Zahl 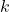 ist
ist  .
. - Ähnliches gilt für die Cosinusfunktion
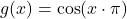 : Ihre Nullstellen liegen bei allen Zahlen
: Ihre Nullstellen liegen bei allen Zahlen  , die sich um
, die sich um 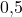 von einer ganzen Zahl
von einer ganzen Zahl 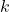 unterscheiden. Denn für jede ganze Zahl
unterscheiden. Denn für jede ganze Zahl 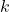 ist
ist  .
. - Die Sinus- und Cosinusfunktion haben also unendlich viele, verschiedene und einzeln liegende Nullstellen.
- Diese Funktionen sind keine Polynomfunktionen. Denn eine Polynomfunktion vom Grad
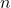 hat höchstens
hat höchstens 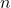 verschiedene Nullstellen.
verschiedene Nullstellen. - Auch jede Sinusfunktion der Form
 und jede Cosinusfunktion der Form
und jede Cosinusfunktion der Form  hat unendlich viele verschiedene, einzeln liegende Nullstellen.
hat unendlich viele verschiedene, einzeln liegende Nullstellen.
Nullstellen – Exponentialfunktionen und Logarithmusfunktionen
- Die Exponentialfunktionen
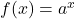 mit
mit 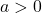 haben keine Nullstellen. Denn Potenzen einer positiven Basis werden niemals null.
haben keine Nullstellen. Denn Potenzen einer positiven Basis werden niemals null. - Exponentialfunktionen und speziell die
 -Funktion schneiden die
-Funktion schneiden die  -Achse nicht.
-Achse nicht.

- Die Logarithmusfunktionen
 zur Basis
zur Basis  mit
mit 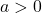 und
und  haben alle genau eine Nullstelle, und zwar alle dieselbe, nämlich
haben alle genau eine Nullstelle, und zwar alle dieselbe, nämlich  . Denn für jede Basis
. Denn für jede Basis 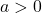 ist
ist 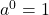 , also
, also  .
.
Nullstellen berechnen – Funktionstypen und Lösungsverfahren
In diesem Abschnitt stellen wir Verfahren zur Berechnung von Nullstellen für verschiedene Funktionstypen vor. Um die Nullstellen einer Funktion ![]() zu berechnen, musst du die Gleichung
zu berechnen, musst du die Gleichung ![]() lösen. Der Typ dieser Gleichung hängt vom Funktionstyp ab. Im Folgenden werden die einzelnen Typen beschrieben.
lösen. Der Typ dieser Gleichung hängt vom Funktionstyp ab. Im Folgenden werden die einzelnen Typen beschrieben.
Nullstellen berechnen – lineare Funktionen
Eine lineare Funktion ist von der Form ![]() mit reellen Koeffizienten
mit reellen Koeffizienten ![]() und
und ![]() . Um die Nullstellengleichung
. Um die Nullstellengleichung ![]() zu lösen, musst du zuerst die Koeffizienten
zu lösen, musst du zuerst die Koeffizienten ![]() und
und ![]() anschauen. Je nach den Werten dieser Koeffizienten ergibt sich folgende Fallunterscheidung für die Bestimmung der Nullstellen:
anschauen. Je nach den Werten dieser Koeffizienten ergibt sich folgende Fallunterscheidung für die Bestimmung der Nullstellen:
- Ist
 , kannst du die Gleichung
, kannst du die Gleichung 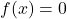 nach der Variablen
nach der Variablen  auflösen:
auflösen:

- Ist
 und
und  , hat
, hat  keine Nullstellen.
keine Nullstellen. - Ist
 und
und  , ist jede reelle Zahl
, ist jede reelle Zahl  eine Nullstelle von
eine Nullstelle von  .
.
Nullstellen berechnen – quadratische Funktionen
- Eine quadratische Funktion ist meistens in allgemeiner Form
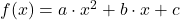 oder in Normalform
oder in Normalform  gegeben.
gegeben. - Außerdem gibt es die Scheitelpunktform, die aber für die Berechnung der Nullstellen nicht direkt verwendbar ist.
- Setzt du den Funktionsterm gleich null, erhältst du aus einer quadratischen Funktion
 eine quadratische Gleichung, die Nullstellengleichung
eine quadratische Gleichung, die Nullstellengleichung 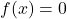 . Diese Gleichung kannst du folgendermaßen lösen:
. Diese Gleichung kannst du folgendermaßen lösen:
Nullstellen berechnen mit der pq-Formel
- Die Nullstellen einer quadratischen Funktion in Normalform
 berechnest du mit der pq-Formel:
berechnest du mit der pq-Formel:

- Ist
 , ist der Wurzelterm nicht definiert. Die Gleichung
, ist der Wurzelterm nicht definiert. Die Gleichung 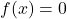 hat keine reelle Lösung und daher hat die Funktion
hat keine reelle Lösung und daher hat die Funktion  keine Nullstelle.
keine Nullstelle. - Ist
 , hat
, hat  die doppelte Nullstelle
die doppelte Nullstelle  .
. - Ist
 , hat
, hat  die beiden verschiedenen Nullstellen
die beiden verschiedenen Nullstellen  und
und  .
.
Schauen wir uns das an einem Beispiel an und berechnen die Nullstellen der Funktion ![]() :
:
- Wir setzen den Funktionsterm gleich null und erhalten die quadratische Gleichung
 .
. - Die Funktion bzw. die quadratische Gleichung liegt in Normalform vor, daher verwenden wir die pq-Formel mit
 und
und  :
:

- Die Funktion
 hat also die beiden verschiedenen Nullstellen
hat also die beiden verschiedenen Nullstellen  und
und  .
.
Nullstellen berechnen mit der Mitternachtsformel
- Die Nullstellen einer quadratischen Funktion in allgemeiner Form
 berechnest du mit der Mitternachtsformel:
berechnest du mit der Mitternachtsformel:

- Ist
 , ist der Wurzelterm nicht definiert. Die Gleichung
, ist der Wurzelterm nicht definiert. Die Gleichung 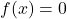 hat keine reelle Lösung und daher hat die Funktion
hat keine reelle Lösung und daher hat die Funktion  keine Nullstelle.
keine Nullstelle. - Ist
 , hat
, hat  die doppelte Nullstelle
die doppelte Nullstelle 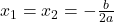 .
. - Ist
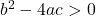 , hat
, hat  die beiden verschiedenen Nullstellen
die beiden verschiedenen Nullstellen  und
und  .
.
Schauen wir uns wieder ein Beispiel an und berechnen die Nullstellen der Funktion ![]() :
:
- Wir setzen den Funktionsterm gleich null und erhalten die quadratische Gleichung
 .
. - Die Funktion bzw. die quadratische Gleichung liegt in allgemeiner Form vor, daher verwenden wir die Mitternachtsformel mit
 ,
,  und
und  :
:

Der Term unter der Wurzel ist negativ, daher existieren die durch die Formel beschriebenen reellen Zahlen
unter der Wurzel ist negativ, daher existieren die durch die Formel beschriebenen reellen Zahlen  und
und  nicht. Die Funktion
nicht. Die Funktion  hat also keine Nullstellen.
hat also keine Nullstellen.
Nullstellen quadratischer Funktionen – Nullstellenform
- Hat eine quadratische Funktion
 eine doppelte Nullstelle
eine doppelte Nullstelle 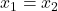 oder zwei verschiedene Nullstellen
oder zwei verschiedene Nullstellen  , kannst du den Funktionsterm von
, kannst du den Funktionsterm von  zur Nullstellenform umformen.
zur Nullstellenform umformen. - Die Nullstellenform lautet:

- Diese Form der quadratischen Funktion
 heißt auch die faktorisierte Form.
heißt auch die faktorisierte Form. - Aus dieser Form kannst du die Nullstellen
 und
und  direkt ablesen.
direkt ablesen.
Nullstellen berechnen – ganzrationale Funktionen höheren Grads
Eine Polynomfunktion ![]() mit
mit ![]() wird auch ganzrationale Funktion vom Grad
wird auch ganzrationale Funktion vom Grad ![]() bezeichnet. Beispielsweise ist
bezeichnet. Beispielsweise ist ![]() eine ganzrationale Funktion vom Grad
eine ganzrationale Funktion vom Grad ![]() .
.
Ist der Grad von ![]() größer als zwei, werden die Nullstellen von
größer als zwei, werden die Nullstellen von ![]() nicht durch eine direkte Formel berechnet. Stattdessen gibt es verschiedene Methoden für die Berechnung der Nullstellen. Alle Methoden beruhen darauf, den Grad der Nullstellengleichung zu reduzieren.
nicht durch eine direkte Formel berechnet. Stattdessen gibt es verschiedene Methoden für die Berechnung der Nullstellen. Alle Methoden beruhen darauf, den Grad der Nullstellengleichung zu reduzieren.
Der Satz vom Nullprodukt
- Ist
 , ist jede Nullstelle von
, ist jede Nullstelle von  auch eine Nullstelle von
auch eine Nullstelle von 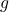 oder von
oder von 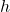 .
. - Der Grad von
 ist die Summe der Grade von
ist die Summe der Grade von 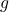 und
und 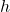 . Die Funktionen
. Die Funktionen 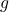 und
und 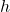 haben also im Allgemeinen einen kleineren Grad als
haben also im Allgemeinen einen kleineren Grad als  .
. - Kannst du die Nullstellen von
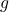 und
und 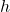 bestimmen, findest du alle Nullstellen von
bestimmen, findest du alle Nullstellen von  .
. - Beispielsweise kann man die Funktion
 umformen zu
umformen zu  . Die Nullstellen der Funktionen
. Die Nullstellen der Funktionen  und
und  kannst du mit der pq-Formel berechnen. So erhältst du alle Nullstellen von
kannst du mit der pq-Formel berechnen. So erhältst du alle Nullstellen von  .
.
Ausklammern von Potenzen
- Den Satz vom Nullprodukt verwendest du meistens dann, wenn du aus dem Funktionsterm Potenzen der Form
 mit
mit  ausklammern kannst.
ausklammern kannst. - Ist
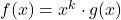 , ist nach dem Satz vom Nullprodukt jede Nullstelle von
, ist nach dem Satz vom Nullprodukt jede Nullstelle von  eine Nullstelle von
eine Nullstelle von  oder eine Nullstelle von
oder eine Nullstelle von  .
. - Für
 ist
ist 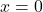 die einzige Nullstelle von
die einzige Nullstelle von  .
. - Nullstellen von
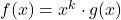 sind also
sind also 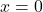 und die Nullstellen von
und die Nullstellen von  .
. - Beispielsweise kannst du aus
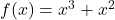 die Potenz
die Potenz 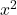 ausklammern:
ausklammern:
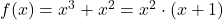
Die Nullstellen von sind demnach
sind demnach  und die Nullstelle von
und die Nullstelle von  , also
, also  .
. - Klammere immer die größtmögliche Potenz von
 aus. Dadurch reduziert sich der Grad derjenigen Funktion, von der du die Nullstellen suchen musst. Im besten Fall kannst du die Nullstellen von
aus. Dadurch reduziert sich der Grad derjenigen Funktion, von der du die Nullstellen suchen musst. Im besten Fall kannst du die Nullstellen von  dann mit einer anderen Methode bestimmen.
dann mit einer anderen Methode bestimmen.
Substitution
- Bei speziellen Gleichungen kannst du eine Potenz der Variablen durch eine neue Variable ersetzen.
- Durch diese Substitution erhältst du eine Gleichung niedrigeren Grads mit der neuen Variablen.
- Kannst du die substituierte Gleichung lösen, erhältst du die Lösungen der ursprünglichen Gleichung der Rücksubstitution.
- Diese Methode funktioniert nur, wenn alle Exponenten der Funktion eine gemeinsamen Teiler haben, der größer als
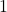 ist.
ist.
Beispiel:
In der biquadratischen Gleichung ![]() sind alle Exponenten durch
sind alle Exponenten durch ![]() teilbar. Dadurch sind alle Potenzen von
teilbar. Dadurch sind alle Potenzen von ![]() , die in der Gleichung vorkommen, auch Potenzen von
, die in der Gleichung vorkommen, auch Potenzen von ![]() .
.
- Substituierst du in der Gleichung
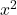 durch die neue Variable
durch die neue Variable 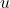 , erhältst du:
, erhältst du:

- Die quadratische Gleichung
 kannst du mit der pq-Formel lösen.
kannst du mit der pq-Formel lösen. - Die Lösungen der Gleichung
 erhältst du durch die Rücksubstitution
erhältst du durch die Rücksubstitution  und
und  aus den Lösungen
aus den Lösungen 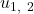 der quadratischen Gleichung
der quadratischen Gleichung  .
.
Polynomdivision
- Die Polynomdivision der Funktion
 durch einen Linearfaktor
durch einen Linearfaktor  reduziert den Grad um
reduziert den Grad um 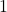 .
. - Die Polynomdivision von
 durch den Linearfaktor
durch den Linearfaktor  geht genau dann ohne Rest auf, wenn
geht genau dann ohne Rest auf, wenn  eine Nullstelle von
eine Nullstelle von  ist.
ist. - Die Nullstellen des Quotienten
 sind auch Nullstellen von
sind auch Nullstellen von  .
. - Hat
 den Grad
den Grad 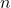 , hat
, hat  den Grad
den Grad  .
. - Hat
 den Grad
den Grad 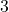 und ist
und ist  eine Nullstelle von
eine Nullstelle von  , ist
, ist  eine quadratische Funktion. Deren Nullstellen lassen sich mit der pq-Formel oder der Mitternachtsformel berechnen.
eine quadratische Funktion. Deren Nullstellen lassen sich mit der pq-Formel oder der Mitternachtsformel berechnen.
Häufig gestellte Fragen zum Thema Nullstellen berechnen

