Der Zylinder in der Mathematik – Geometrie und Berechnung

Erfahre alles über Zylinder: Definition, Eigenschaften, Berechnungen und spezielle Arten. Ein Zylinder besteht aus kongruenten Kreisen als Grund- und Deckfläche, verbunden durch die Mantelfläche. Wie berechnet man Oberfläche und Volumen?

Inhaltsverzeichnis zum Thema Zylinder

Der Zylinder im Überblick

  • Der Zylinder ist ein geometrischer Körper.
  • Ein Zylinder hat drei Flächen, zwei Kanten und keine Ecken.
  • Die Grund- und die Deckfläche des Zylinders sind kreisförmig, zueinander kongruent und parallel.
Zylinder: Lernvideo

Quelle sofatutor.com

Zylinder – Definition

Bei einem Zylinder (auch Kreiszylinder) handelt es sich um einen geometrischen Körper. Die Grund- und die Deckfläche sind zueinander kongruente und parallele Kreise. Die Seitenfläche eines Zylinders wird als Mantel oder Mantelfläche bezeichnet, da sie die beiden Kreise ummantelt. Als Höhe h des Zylinders wird der Abstand zwischen den Ebenen der Grund- und der Deckfläche bezeichnet.
Der Radius r des Zylinders ist der Abstand des Mittelpunkts der Grund- oder Deckfläche zu ihrem Rand.

Zylinder

Hinweis: Wird von einem Zylinder gesprochen, ist meist der gerade Zylinder gemeint. Im folgenden Text sind ebenfalls die geraden Zylinder gemeint, wenn von einem Zylinder die Rede ist.

Zylinder – Eigenschaften

Zylinder sind durch besondere Merkmale und Eigenschaften definiert. Für alle geraden Zylinder gilt:

  • Zwei zueinander kongruente und parallele Kreise bilden die Grund- und Deckfläche.
  • Die Deckfläche liegt genau über der Grundfläche.
  • Die Grund- und Deckfläche werden durch die Mantelfläche miteinander verbunden.
  • Die Mantelfläche verläuft senkrecht zu den Kreisflächen.
  • Ausgebreitet hat die Mantelfläche die Form eines Rechtecks.
  • Ein Zylinder hat drei Flächen, zwei Kanten und keine Ecken.

Das folgende Bild zeigt das Körpernetz eines Zylinders. Es ist erkennbar, dass die Mantelfläche ausgebreitet die Form eines Rechtecks hat.



Körpernetz Zylinder

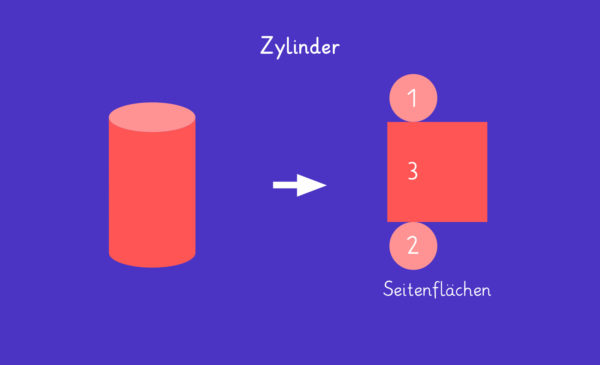
Besondere Zylinder

Neben dem (geraden) Zylinder existieren auch Zylinder mit einer besonderen Form. Die wichtigsten sind:

Der schiefe Zylinder

  • Deckflächen sind zueinander verschoben. 
  • Höhe entspricht nicht der Verbindung der Mittelpunkte der Kreisflächen, sondern dem Abstand des Mittelpunkts der Grundfläche zur Ebene, in der die Deckfläche liegt.
  • Mantelfläche ergibt ausgebreitet kein Rechteck.

Der offene Zylinder

  • Er ist nur auf einer Seite geschlossen. 
  • Er hat keine Deckfläche.

Der Hohlzylinder

  • Zylinder, aus dem mittig ein kleinerer Zylinder ausgeschnitten wurde
  • Der innere Zylinder hat die gleiche Höhe wie der äußere Zylinder.
  • Der Zylinder ist also in der Mitte hohl (er besitzt ein Loch).

Zylinder – Berechnungen

Schauen wir uns nun an, wie wir die Oberfläche und das Volumen eines (geraden) Zylinders berechnen können.

Oberfläche eines Zylinders – Formel

Die Oberfläche eines Zylinders wird durch die kreisförmige Grund- und Deckfläche sowie die Mantelfläche gebildet. Die Grund- und die Deckfläche sind genau gleich groß. Also ist die Oberfläche die Summe aus der doppelten Grundfläche und der Mantelfläche:

\text{Oberfläche} = 2 \cdot \text{Grundfläche} + \text{Mantelfläche} = 2G + M

Für die kreisförmige Grundfläche gilt:

G = \pi \cdot r^2

Dabei ist r der Radius der Grundfläche des Zylinders.

Für die rechteckige Mantelfläche gilt:

M = 2\pi \cdot r \cdot h

Dabei ist 2\pi \cdot r der Umfang der Grundfläche des Zylinders und h die Höhe des Zylinders.

Die Oberfläche des Zylinders hängt somit vom Radius der Grundfläche und von der Höhe des Zylinders ab. Um die Oberfläche eines Zylinders zu berechnen, nutzen wir die Formel:

O = 2 \cdot \pi \cdot r^2 + 2\pi \cdot r \cdot h = 2 \pi r \cdot (r + h)

Die Einheit der Oberfläche eines Zylinders hängt von den Einheiten ab, in denen der Radius und die Höhe gegeben sind. Wie alle Flächen wird die Oberfläche immer in Flächeneinheiten (Quadratmeter, Quadratzentimeter …) angegeben.

Beispiel
Berechne die Oberfläche eines Zylinders mit der Höhe h = 5~\text{cm} und dem Radius r = 6~\text{cm}.

O = 2 \pi r \cdot (r + h) = 2 \pi \cdot 6~\text{cm} \cdot (6~\text{cm} + 5~\text{cm}) \approx 414{,}7~\text{cm}^2

Oberfläche eines Zylinders – Rechner



Volumen eines Zylinders – Formel

Um das Volumen eines Zylinders zu berechnen, wird der Flächeninhalt der Grundfläche mit der Höhe multipliziert:

\text{Volumen} = \text{Grundfläche} \cdot \text{Höhe} = G \cdot h

Das Volumen ist ebenfalls abhängig vom Radius r der Grundfläche und der Höhe h des Zylinders. Die Formel zur Berechnung des Volumens eines Zylinders lautet:

V = G \cdot h = \pi \cdot r^2 \cdot h

Diese Formel gilt auch für den schiefen Zylinder, allerdings ist die Höhe h bei einem schiefen Zylinder anders zu bestimmen.

Die Einheit des Volumens eines Zylinders hängt von den Einheiten ab, in denen der Radius und die Höhe gegeben sind. Wie das Volumen von anderen Körpern wird auch dieses Volumen immer in Raumeinheiten (Kubikmeter, Kubikzentimeter …) angegeben.

Beispiel
Berechne das Volumen eines Zylinders mit der Höhe h = 2~\text{cm} und dem Radius r = 4~\text{cm}.

V = \pi \cdot r^2 \cdot h = \pi \cdot \left(4~\text{cm}\right)^2 \cdot 2~\text{cm} \approx 100{,}5~\text{cm}^3

Volumen eines Zylinders – Rechner



Berechnungen eines Hohlzylinders

Die Oberfläche O_h eines Hohlzylinders ist die Summe aus der Mantelfläche des äußeren Zylinders M_a und der Mantelfläche des inneren Zylinders M_i und der Fläche der Kreisringe G_r:

O_h = M_a + M_i + 2G_r

Die Fläche der Kreisringe ergibt sich, indem wir die Fläche des kleineren Kreises von der des größeren Kreises abziehen.

G_r = G_a - G_i

Um das Volumen eines Hohlzylinders zu berechnen, wird das Volumen V_i des inneren, ausgeschnittenen Zylinders vom äußeren, größeren Zylinder V_a abgezogen.

V_h = V_a - V_i

Beispiel
Berechne die Oberfläche und das Volumen eines Hohlzylinders mit den folgenden Maßen:
Äußerer Zylinder: h = 4~\text{cm} und R = 5~\text{cm}
Innerer Zylinder: h = 4~\text{cm} und r = 3~\text{cm}

Für die Oberfläche gilt: O_h = M_a + M_i + 2G_r

M_a = 2\pi \cdot R \cdot h = 2\pi \cdot 5~\text{cm} \cdot 4~\text{cm} \approx 125{,}7~\text{cm}^2
M_i = 2\pi \cdot r \cdot h = 2\pi \cdot 3~\text{cm} \cdot 4~\text{cm} \approx 75{,}4~\text{cm}^2
G_r = \pi \cdot R^2 - \pi \cdot r^2 = \pi \cdot \left(5~\text{cm}\right)^2 - \pi \cdot \left(3~\text{cm}\right)^2 \approx 50{,}3~\text{cm}^2

O_h = 125{,}7~\text{cm}^2 + 75{,}4~\text{cm}^2 + 2 \cdot 50{,}3~\text{cm}^2 = 301{,}7~\text{cm}^2

Für das Volumen gilt: V_h = V_a - V_i

V_a = \pi \cdot R^2 \cdot h = \pi \cdot \left(5~\text{cm}\right)^2 \cdot 4~\text{cm} \approx 314{,}2~\text{cm}^3
V_i = \pi \cdot r^2 \cdot h = \pi \cdot \left(3~\text{cm}\right)^2 \cdot 4~\text{cm} \approx 113{,}1~\text{cm}^3

V_h = 314{,}2~\text{cm}^3 - 113{,}1~\text{cm}^3 = 201{,}1~\text{cm}^3

Berechnungen mit Zylindern – Anwendungen

Hier kannst du die Formeln an einige Aufgaben zur Berechnung von Zylindern direkt selbst anwenden.

Aufgabe 1
Berechne die Oberfläche und das Volumen des dargestellten Zylinders.

Zylinder Berechnungen

Lösung Aufgabe 1
Gegeben:
r = 4~\text{cm}
h = 7~\text{cm}

Gesucht: Oberfläche und Volumen

Berechnung der Oberfläche:
O = 2 \pi r \cdot (r + h) = 2 \pi \cdot 4~\text{cm} \cdot (4~\text{cm} + 7~\text{cm}) \approx 276{,}5~\text{cm}^2

Berechnung Volumen:
V = \pi \cdot r^2 \cdot h = \pi \cdot \left(4~\text{cm}\right)^2 \cdot 7~\text{cm} \approx 351{,}9~\text{cm}^3

Antwortsatz:
Der dargestellte Zylinder hat eine Oberfläche von 276{,}5~\text{cm}^2 und ein Volumen von 351{,}9~\text{cm}^3.

Aufgabe 2
Berechne die Oberfläche und das Volumen des dargestellten Hohlzylinders.

Hohlzylinder Berechnungen

Lösung Aufgabe 2
Gegeben:
h = 6~\text{cm}
R = 4~\text{cm}
r = 4~\text{cm} - 1~\text{cm} = 3~\text{cm}

Gesucht: Oberfläche und Volumen

Berechnung Oberfläche:
O_h = M_a + M_i + 2G_r

M_a = 2\pi \cdot R \cdot h = 2\pi \cdot 4~\text{cm} \cdot 6~\text{cm} \approx 150{,}8~\text{cm}^2
M_i = 2\pi \cdot r \cdot h = 2\pi \cdot 3~\text{cm} \cdot 6~\text{cm} \approx 113{,}1~\text{cm}^2
G_r = \pi \cdot R^2 - \pi \cdot r^2 = \pi \cdot \left(4~\text{cm}\right)^2 - \pi \cdot \left(3~\text{cm}\right)^2 \approx 22{,}0~\text{cm}^2

O_h = 150{,}8~\text{cm}^2 + 113{,}1~\text{cm}^2 + 2 \cdot 22{,}0~\text{cm}^2 = 307{,}9~\text{cm}^2

Berechnung Volumen:
V_h = V_a - V_i

V_a = \pi \cdot R^2 \cdot h = \pi \cdot \left(4~\text{cm}\right)^2 \cdot 6~\text{cm} \approx 301{,}6~\text{cm}^3
V_i = \pi \cdot r^2 \cdot h = \pi \cdot \left(3~\text{cm}\right)^2 \cdot 6~\text{cm} \approx 169{,}6~\text{cm}^3

V_h = 301{,}6~\text{cm}^3 - 169{,}6~\text{cm}^3 = 132{,}0~\text{cm}^3

Antwortsatz:
Der dargestellte Hohlzylinder hat eine Oberfläche von 307{,}9~\text{cm}^2 und ein Volumen von 132{,}0~\text{cm}^3.

Häufig gestellte Fragen zum Thema Zylinder

Ein Zylinder ist ein geometrischer Körper, der eine kreisförmige Grundfläche und eine kreisförmige Deckfläche besitzt, die durch die sogenannte Mantelfläche verbunden sind.

Die Grund- und die Deckfläche eines Zylinders sind zueinander kongruente, parallele Kreisflächen. Verbunden werden sie durch die Mantelfläche. Ein Zylinder hat somit drei Flächen, zwei Kanten und keine Ecken.

Die Mantelfläche eines Zylinders ist die Seitenfläche, die die Grund- und Deckfläche miteinander verbindet. Bei geraden Zylindern bildet die Mantelfläche im aufgeklappten Zustand ein Rechteck.

Bei einem geraden Zylinder entspricht die Mantelfläche der Höhe multipliziert mit dem Umfang der Grundfläche. Für die Mantelfläche gilt:
M = 2\pi \cdot r \cdot h

Der Radius des Zylinders entspricht dem Radius der Grundfläche. Das ist der Abstand zwischen dem Mittelpunkt der Grundfläche und dem Rand der Grundfläche. Der Radius wird mit r abgekürzt.

Der Durchmesser des Zylinders entspricht dem Durchmesser der Grundfläche. Für den Durchmesser d gilt:
d = 2 \cdot r

Die Höhe eines Zylinders ist der Abstand zwischen der Grund- und der Deckfläche. Bei einem geraden Zylinder entspricht das dem Abstand zwischen den Mittelpunkten der Kreisflächen.

Um die Oberfläche eines Zylinders zu berechnen, werden die Flächeninhalte der drei Flächen addiert:
O = 2G + M

Die Formel zur Berechnung der Oberfläche eines Zylinder lautet:
O = 2 \pi r \cdot (r + h)

Um das Volumen eines Zylinders zu berechnen, wird die Grundfläche mit der Höhe multipliziert.

Die Formel zur Berechnung des Volumens eines Zylinders lautet:
V = G \cdot h = \pi \cdot r^2 \cdot h

Leave A Comment

Alle Artikel aus dem Fach Mathematik