Spurpunkte in der Mathematik
Entdecke die Schnittpunkte einer Geraden mit den Koordinatenebenen. Erfahre, wie man Spurpunkte bestimmt und berechnet.
Inhaltsverzeichnis zum Thema Spurpunkte
Spurpunkte im Überblick
Definition von Spurpunkten – Durchstoßpunkt einer Geraden durch eine Ebene
Die Koordinatenachsen spannen den dreidimensionalen Raum auf. Jeweils zwei Achsen spannen eine Ebene auf. Diese Ebenen werden Koordinatenebenen genannt.

In dieser Abbildung sind die Koordinatenachsen mit ![]() ,
, ![]() und
und ![]() benannt. Eine Bezeichnung mit
benannt. Eine Bezeichnung mit ![]() ,
,![]() und
und ![]() ist ebenfalls möglich.
ist ebenfalls möglich.
Bei Punkten, die in einer Koordinatenebene liegen, hat die Koordinate der Achse, die aus der Ebene herausragt, immer den Wert ![]() . Für die
. Für die ![]() –
–![]() -Ebene gilt daher die Gleichung
-Ebene gilt daher die Gleichung ![]() , für die
, für die ![]() –
–![]() -Ebene die Gleichung
-Ebene die Gleichung ![]() und für die
und für die ![]() –
–![]() -Ebene die Gleichung
-Ebene die Gleichung ![]() .
.
Spurpunkte sind die Schnittpunkte einer Geraden mit den Koordinatenebenen.
Betrachte in der folgenden Abbildung die Gerade und ihre Spurpunkte. Der Durchstoßpunkt der Geraden durch die ![]() –
–![]() -Ebene wird mit
-Ebene wird mit ![]() bezeichnet, der Durchstoßpunkt durch die
bezeichnet, der Durchstoßpunkt durch die ![]() –
–![]() -Ebene heißt
-Ebene heißt ![]() und der Durchstoßpunkt durch die
und der Durchstoßpunkt durch die ![]() –
–![]() -Ebene ist
-Ebene ist ![]() .
.
Auch hier sind abweichende Notationen wie ![]() ,
, ![]() und
und ![]() möglich.
möglich.

Die Gerade in der Abbildung besitzt drei Spurpunkte.
Eine Gerade kann entweder einen, zwei, drei oder unendlich viele Spurpunkte haben.
| Anzahl Spurpunkte | Lage der Geraden |
|---|---|
| Die Gerade verläuft parallel zu einer der Koordinatenachsen, liegt aber nicht auf dieser. | |
| Die Gerade verläuft parallel zu einer Koordinatenebene, liegt aber nicht in dieser. | |
| Die Gerade verläuft nicht parallel zu einer der Koordinatenebenen oder Koordinatenachsen. | |
| unendlich viele | Die Gerade verläuft innerhalb einer Koordinatenebene bzw. auf einer Koordinatenachse. |
Spurpunkte bestimmen und berechnen
Um die Spurpunkte einer Geraden zu bestimmen, setzt du in der Parameterform der Geradengleichung die ![]() -,
-, ![]() – oder
– oder ![]() – Koordinate gleich null. Dadurch erhältst du jeweils eine Gleichung, die du nach dem Parameter auflöst. Den Wert, den du für den Parameter erhältst, setzt du in die Geradengleichung ein und hast so den Spurpunkt ermittelt.
– Koordinate gleich null. Dadurch erhältst du jeweils eine Gleichung, die du nach dem Parameter auflöst. Den Wert, den du für den Parameter erhältst, setzt du in die Geradengleichung ein und hast so den Spurpunkt ermittelt.
Betrachte beispielhaft die Gerade ![]() :
:

Um die Spurpunkte der Geraden ![]() zu berechnen, setzt du jeweils eine Koordinate gleich null.
zu berechnen, setzt du jeweils eine Koordinate gleich null.
- Den Schnittpunkt mit der
 –
– -Ebene erhältst du, indem du
-Ebene erhältst du, indem du  setzt. In der dritten Komponente des Vektors
setzt. In der dritten Komponente des Vektors  erhältst du eine Gleichung, die du nach dem Parameter
erhältst du eine Gleichung, die du nach dem Parameter  auflösen kannst:
auflösen kannst:
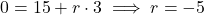
Setzt du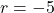 in die Geradengleichung ein, erhältst du den Spurpunkt
in die Geradengleichung ein, erhältst du den Spurpunkt  :
:
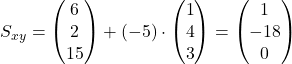
- Den Schnittpunkt mit der
 –
– -Ebene erhältst du, indem du
-Ebene erhältst du, indem du 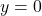 setzt. Diesmal erhältst du in der zweiten Komponente von
setzt. Diesmal erhältst du in der zweiten Komponente von  eine Gleichung, die du nach
eine Gleichung, die du nach  auflösen kannst:
auflösen kannst:
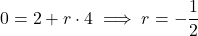
Setze in die Geradengleichung ein und du findest den Spurpunkt
in die Geradengleichung ein und du findest den Spurpunkt  :
:

- Den Schnittpunkt mit der
 –
– -Ebene erhältst du, indem du
-Ebene erhältst du, indem du 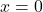 setzt. Hier erhältst du eine Gleichung in der ersten Komponente von
setzt. Hier erhältst du eine Gleichung in der ersten Komponente von  :
:

Setze in die Geradengleichung ein, um den Spurpunkt
in die Geradengleichung ein, um den Spurpunkt 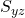 zu bestimmen:
zu bestimmen:

Spurgerade einer Ebene
Ähnlich wie Spurpunkte von Geraden gibt es Spurgeraden von Ebenen.
Die Schnittmenge einer Ebene ![]() mit einer Koordinatenebene ist kein Punkt, sondern eine Schnittgerade.
mit einer Koordinatenebene ist kein Punkt, sondern eine Schnittgerade.
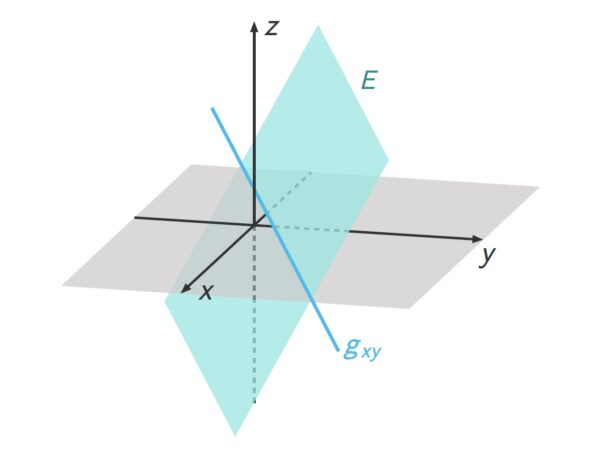
In der Abbildung wird die Schnittgerade der Ebene ![]() mit der
mit der ![]() –
–![]() -Ebene durch die Gerade
-Ebene durch die Gerade ![]() dargestellt.
dargestellt.
Spurgeraden sind also die Schnittgeraden einer Ebene mit den Koordinatenebenen.
Aufgabe Spurpunkte berechnen – Schattenpunkt berechnen
Spurpunkte werden verwendet, um Schattenwürfe zu berechnen. Du kannst beispielsweise berechnen, wo der Schatten einer Kirchturmspitze auf den Boden trifft.
Die Kirchturmspitze befindet sich im Punkt ![]() , der Boden liegt in der
, der Boden liegt in der ![]() –
–![]() -Ebene und die einfallenden Lichtstrahlen haben die Richtung des Vektors
-Ebene und die einfallenden Lichtstrahlen haben die Richtung des Vektors ![]() .
.
Der gesuchte Schatten der Turmspitze liegt dort, wo ein Lichtstrahl, der die Spitze des Kirchturms streift, auf den Boden fällt. Dies entspricht dem Spurpunkt einer Geraden ![]() in der
in der ![]() –
–![]() -Ebene des Bodens, die durch den Punkt
-Ebene des Bodens, die durch den Punkt ![]() in Richtung der Lichtstrahlen verläuft.
in Richtung der Lichtstrahlen verläuft.
Wir stellen die Gleichung der Geraden ![]() auf, indem wir
auf, indem wir ![]() als Stützvektor und die Richtung der Lichtstrahlen als Richtungsvektor wählen:
als Stützvektor und die Richtung der Lichtstrahlen als Richtungsvektor wählen:

Um den Schattenpunkt zu berechnen, setzt du nun die ![]() -Koordinate gleich null und löst die Gleichung nach dem Parameter
-Koordinate gleich null und löst die Gleichung nach dem Parameter ![]() auf:
auf:
![]()
Diesen Wert für ![]() setzt du in die Gleichung von
setzt du in die Gleichung von ![]() ein. Der Spurpunkt
ein. Der Spurpunkt ![]() ist der gesuchte Schattenpunkt der Turmspitze:
ist der gesuchte Schattenpunkt der Turmspitze:

Der Schatten der Kirchturmspitze ![]() trifft im Spurpunkt
trifft im Spurpunkt ![]() in der
in der ![]() –
–![]() -Ebene auf den Boden. Dieser Punkt liegt bei:
-Ebene auf den Boden. Dieser Punkt liegt bei:
![]()
Häufig gestellte Fragen zum Thema Spurpunkte
