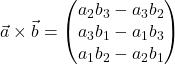Das Kreuzprodukt – Formel, Herleitung und Anwendungen
Erfahre, wie das Kreuzprodukt zweier Vektoren einen neuen Vektor erzeugt, der senkrecht zu beiden steht. Entdecke Anwendungen wie die Bestimmung senkrechter Vektoren und Flächeninhalte von Parallelogrammen. Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Kreuzprodukt
Definition des Kreuzprodukts
Das Kreuzprodukt bezeichnet eine Rechenoperation, die aus zwei Vektoren ![]() und
und ![]() im dreidimensionalen Vektorraum einen neuen Vektor
im dreidimensionalen Vektorraum einen neuen Vektor ![]() macht. Man bezeichnet das Kreuzprodukt auch als Vektorprodukt. Oft bezeichnet man als Kreuzprodukt von Vektoren nicht nur die Rechenoperation selbst, sondern auch ihr Ergebnis: Der Vektor
macht. Man bezeichnet das Kreuzprodukt auch als Vektorprodukt. Oft bezeichnet man als Kreuzprodukt von Vektoren nicht nur die Rechenoperation selbst, sondern auch ihr Ergebnis: Der Vektor ![]() ist das Kreuzprodukt der Vektoren
ist das Kreuzprodukt der Vektoren ![]() und
und ![]() .
.
Zu unterscheiden ist das Kreuzprodukt vom Skalarprodukt, das aus zwei Vektoren ![]() und
und ![]() die Zahl oder den Skalar
die Zahl oder den Skalar ![]() berechnet.
berechnet.
Zur Definition des Vektorprodukts gehen wir von Vektoren ![]() und
und ![]() in Komponentenschreibweise aus:
in Komponentenschreibweise aus:

In Koordinatenschreibweise kannst du nun das Kreuzprodukt ![]() einfach berechnen:
einfach berechnen:
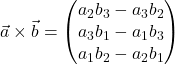
Diese Formel definiert den Vektor ![]() .
.
Kreuzprodukt – Rechenregeln und Eigenschaften
Das Kreuzprodukt ![]() von Vektoren im dreidimensionalen Raum hat viele nützliche Eigenschaften:
von Vektoren im dreidimensionalen Raum hat viele nützliche Eigenschaften:
 steht senkrecht auf
steht senkrecht auf  und auf
und auf 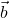 .
.- Die Vektoren
 ,
, 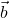 und
und  bilden eine rechtshändig orientierte Basis (sofern
bilden eine rechtshändig orientierte Basis (sofern  und
und 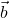 linear unabhängig sind).
linear unabhängig sind). - Das Kreuzprodukt der beiden ersten Standardbasisvektoren
 und
und 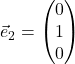 ist der dritte Standardbasisvektor:
ist der dritte Standardbasisvektor:
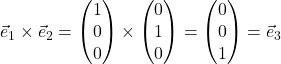
- Vertauschst du die Reihenfolge von
 und
und 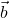 , ändert sich beim Kreuzprodukt das Vorzeichen, d. h.
, ändert sich beim Kreuzprodukt das Vorzeichen, d. h.  . Das Kreuzprodukt ist also nicht kommutativ.
. Das Kreuzprodukt ist also nicht kommutativ. - Skalierst du einen der beiden Vektoren
 oder
oder 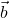 mit einem Faktor
mit einem Faktor  , skaliert sich auch das Kreuzprodukt:
, skaliert sich auch das Kreuzprodukt:
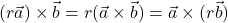
Man sagt: Das Kreuzprodukt ist bilinear bzw. linear in jedem Faktor einzeln. - Das Kreuzprodukt erfüllt das folgende Distributivgesetz:

- Das Kreuzprodukt paralleler Vektoren ist immer null.
- Das Kreuzprodukt von Einheitsvektoren (d. h. Vektoren der Länge
 )
)  und
und 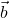 ist nur dann ein Einheitsvektor, wenn
ist nur dann ein Einheitsvektor, wenn  und
und 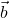 orthogonal zueinander sind.
orthogonal zueinander sind. - Der Betrag des Kreuzprodukts
 ist der Flächeninhalt
ist der Flächeninhalt 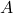 des von den Vektoren
des von den Vektoren  und
und 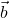 aufgespannten Parallelogramms.
aufgespannten Parallelogramms. - Drei Vektoren
 ,
, 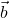 und
und  spannen einen Spat auf – so etwas wie ein dreidimensionales Parallelogramm. Das Volumen
spannen einen Spat auf – so etwas wie ein dreidimensionales Parallelogramm. Das Volumen 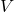 des Spats berechnest du mit dem Kreuzprodukt und dem Skalarprodukt:
des Spats berechnest du mit dem Kreuzprodukt und dem Skalarprodukt:

Dieses Produkt aus drei Vektoren trägt daher auch den Namen Spatprodukt.
Gegeben sind zwei Vektoren  und
und  , gesucht ist ein Vektor
, gesucht ist ein Vektor  , der senkrecht auf
, der senkrecht auf ![]() und senkrecht auf
und senkrecht auf ![]() steht. Wir leiten eine Formel für diesen Vektor
steht. Wir leiten eine Formel für diesen Vektor ![]() her.
her.
Die Orthogonalität von Vektoren ![]() und
und ![]() bezeichnen wir mit
bezeichnen wir mit ![]() . Dass die Vektoren
. Dass die Vektoren ![]() und
und ![]() aufeinander senkrecht stehen, ist äquivalent dazu, dass für ihr Skalarprodukt gilt:
aufeinander senkrecht stehen, ist äquivalent dazu, dass für ihr Skalarprodukt gilt:
![]()
Die Bedingungen ![]() und
und ![]() schreiben wir daher als Gleichungen der Skalarprodukte:
schreiben wir daher als Gleichungen der Skalarprodukte:
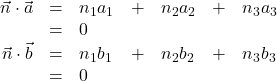
In diesem linearen Gleichungssystem für das Kreuzprodukt sind die Komponenten ![]() ,
, ![]() ,
, ![]() und
und ![]() ,
, ![]() ,
, ![]() der gegebenen Vektoren die Koeffizienten und die Komponenten des Kreuzprodukts
der gegebenen Vektoren die Koeffizienten und die Komponenten des Kreuzprodukts ![]() ,
, ![]() und
und ![]() sind die Variablen. Das Gleichungssystem hat zwei Gleichungen mit den drei Variablen
sind die Variablen. Das Gleichungssystem hat zwei Gleichungen mit den drei Variablen ![]() ,
, ![]() und
und ![]() . Das Gleichungssystem hat daher unendlich viele Lösungen. Das Kreuzprodukt ist also neben der Orthogonalität der Vektoren nur durch eine weitere Bedingung eindeutig festgelegt. Oder anders gesagt: Wir werden während der Herleitung eine der Variablen frei wählen können. Dies wird die Variable
. Das Gleichungssystem hat daher unendlich viele Lösungen. Das Kreuzprodukt ist also neben der Orthogonalität der Vektoren nur durch eine weitere Bedingung eindeutig festgelegt. Oder anders gesagt: Wir werden während der Herleitung eine der Variablen frei wählen können. Dies wird die Variable ![]() sein.
sein.
Um das Gleichungssystem zu lösen, eliminieren wir zuerst die Variable ![]() . Dazu multiplizieren wir die erste Gleichung mit
. Dazu multiplizieren wir die erste Gleichung mit ![]() und subtrahieren sie von der mit
und subtrahieren sie von der mit ![]() multiplizierten zweiten Gleichung. Wir erhalten dann die neue Gleichung:
multiplizierten zweiten Gleichung. Wir erhalten dann die neue Gleichung:
![]()
Nun klammern wir ![]() und
und ![]() aus und bringen alle
aus und bringen alle ![]() -Terme auf die linke Seite der Gleichung:
-Terme auf die linke Seite der Gleichung:
![]()
Als Nächstes dividieren wir beide Seiten der Gleichung durch den Faktor von ![]() auf der linken Seite und erhalten:
auf der linken Seite und erhalten:
![]()
Nun benutzen wir, dass die Variable ![]() frei wählbar ist. Die obige Gleichung für
frei wählbar ist. Die obige Gleichung für ![]() wird viel einfacher, wenn wir als
wird viel einfacher, wenn wir als ![]() den Nenner der rechten Seite wählen, also wenn wir setzen:
den Nenner der rechten Seite wählen, also wenn wir setzen:
![]()
Denn damit kürzt sich der Term für ![]() und wir erhalten in der Gleichung für
und wir erhalten in der Gleichung für ![]() :
:
![]()
Jetzt haben wir schon zwei der drei Komponenten bestimmt. Die Komponente ![]() erhalten wir, indem wir die Formeln für
erhalten wir, indem wir die Formeln für ![]() und
und ![]() in eine der beiden ursprünglichen Gleichungen einsetzen. Wir wählen hier erste Gleichung und setzen
in eine der beiden ursprünglichen Gleichungen einsetzen. Wir wählen hier erste Gleichung und setzen ![]() und
und ![]() dort ein:
dort ein:
![]()
Um ![]() zu bestimmen, lösen wir diese Gleichung zuerst nach
zu bestimmen, lösen wir diese Gleichung zuerst nach ![]() auf und multiplizieren die Klammern aus:
auf und multiplizieren die Klammern aus:
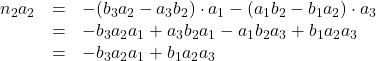
Dabei sind im letzten Schritt beide mittleren Terme weggefallen, denn sie sind identisch bis auf das Vorzeichen. Aus dem Term auf der rechten Seite können wir ![]() ausklammern und erhalten:
ausklammern und erhalten:
![]()
Wir dividieren diese Gleichung noch durch ![]() und erhalten schließlich:
und erhalten schließlich:
![]()
Damit haben wir Formeln für alle drei Komponenten des Kreuzprodukts hergeleitet. Das Kreuzprodukt ![]() ist also:
ist also:

Kreuzprodukt – Anwendungen
Mithilfe des Kreuzprodukts kannst du:
- senkrechte Vektoren bestimmen,
- eine rechtshändig orientierte Basis eines dreidimensionalen Vektorraums konstruieren,
- den Flächeninhalt eines von zwei Vektoren aufgespannten Parallelogramms berechnen und
- das Volumen eines von drei Vektoren aufgespannten Spats berechnen.
Kreuzprodukt – senkrechte Vektoren bestimmen
Sind die Vektoren ![]() und
und ![]() gegeben, kannst du mit dem Kreuzprodukt einen Vektor
gegeben, kannst du mit dem Kreuzprodukt einen Vektor ![]() berechnen, der sowohl auf
berechnen, der sowohl auf ![]() als auch auf
als auch auf ![]() senkrecht steht. Wir berechnen als Beispiel das Kreuzprodukt von
senkrecht steht. Wir berechnen als Beispiel das Kreuzprodukt von 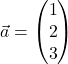 und
und 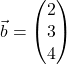 :
:

Dieser Vektor steht senkrecht auf ![]() :
:

Der Vektor ![]() steht auch senkrecht auf
steht auch senkrecht auf ![]() :
:
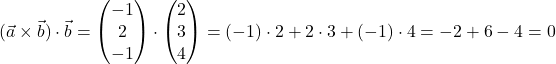
Kreuzprodukt – rechtshändig orientierte Basis bestimmen
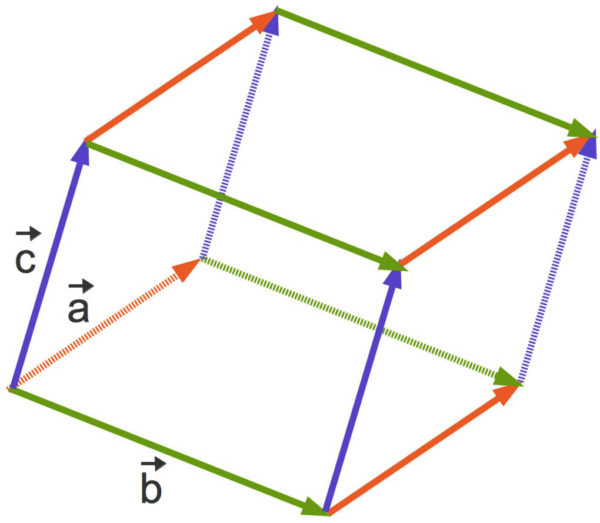
Sind die Vektoren ![]() und
und ![]() linear unabhängig, bilden die Vektoren
linear unabhängig, bilden die Vektoren ![]() ,
, ![]() und
und ![]() zusammen eine rechtshändig orientierte Basis im dreidimensionalen Raum
zusammen eine rechtshändig orientierte Basis im dreidimensionalen Raum ![]() . Um eine solche Basis zu bestimmen, brauchst du also nur zwei Vektoren
. Um eine solche Basis zu bestimmen, brauchst du also nur zwei Vektoren ![]() und
und ![]() , die nicht Vielfache voneinander sind. Diese beiden Vektoren kannst du als Basisvektoren verwenden. Nimmst du das Kreuzprodukt
, die nicht Vielfache voneinander sind. Diese beiden Vektoren kannst du als Basisvektoren verwenden. Nimmst du das Kreuzprodukt ![]() als dritten Vektor dazu, erhältst du die rechtshändig orientierte Basis
als dritten Vektor dazu, erhältst du die rechtshändig orientierte Basis ![]() ,
, ![]() ,
, ![]() .
.
Sind die Vektoren ![]() und
und ![]() Einheitsvektoren und orthogonal zueinander, ist auch das Kreuzprodukt
Einheitsvektoren und orthogonal zueinander, ist auch das Kreuzprodukt ![]() ein Einheitsvektor und orthogonal zu den beiden anderen. Sind die Einheitsvektoren
ein Einheitsvektor und orthogonal zu den beiden anderen. Sind die Einheitsvektoren ![]() und
und ![]() nicht orthogonal zueinander, ist das Kreuzprodukt der Einheitsvektoren kein Einheitsvektor.
nicht orthogonal zueinander, ist das Kreuzprodukt der Einheitsvektoren kein Einheitsvektor.
Kreuzprodukt – Flächeninhalt eines Parallelogramms berechnen
Zwei Vektoren ![]() und
und ![]() spannen ein Parallelogramm in der Ebene auf. Diese Ebene ist im Allgemeinen keine Koordinatenebene, sondern eine schräge Ebene im Raum, die von den Vektoren
spannen ein Parallelogramm in der Ebene auf. Diese Ebene ist im Allgemeinen keine Koordinatenebene, sondern eine schräge Ebene im Raum, die von den Vektoren ![]() und
und ![]() aufgespannt wird. Wir können das Kreuzprodukt geometrisch interpretieren: Der Betrag des Vektors
aufgespannt wird. Wir können das Kreuzprodukt geometrisch interpretieren: Der Betrag des Vektors ![]() ist der Flächeninhalt des von
ist der Flächeninhalt des von ![]() und
und ![]() aufgespannten Parallelogramms:
aufgespannten Parallelogramms:
![]()

Als Beispiel berechnen wir den Flächeninhalt ![]() des von den Vektoren
des von den Vektoren  und
und 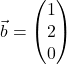 aufgespannten Parallelogramms:
aufgespannten Parallelogramms:

Kreuzprodukt – Volumen eines Spats berechnen
Drei Vektoren ![]() ,
, ![]() und
und ![]() spannen im dreidimensionalen Raum ein Parallelotop oder einen Spat auf. Wir erhalten hier eine weitere geometrische Interpretation des Kreuzprodukts: Das Volumen
spannen im dreidimensionalen Raum ein Parallelotop oder einen Spat auf. Wir erhalten hier eine weitere geometrische Interpretation des Kreuzprodukts: Das Volumen ![]() des Spats lässt sich durch die folgende Formel aus dem Kreuzprodukt und dem Skalarprodukt berechnen:
des Spats lässt sich durch die folgende Formel aus dem Kreuzprodukt und dem Skalarprodukt berechnen:
![]()
Wir berechnen als Beispiel das Volumen ![]() des von den Vektoren
des von den Vektoren 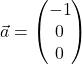 und
und  und
und  aufgespannten Parallelotops:
aufgespannten Parallelotops:
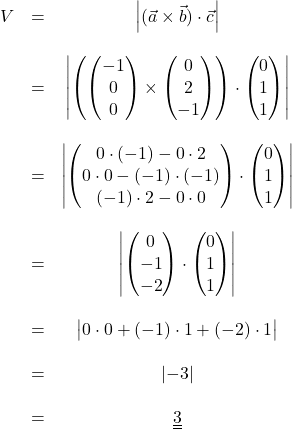
Häufig gestellte Fragen zum Thema Kreuzprodukt

 und
und  berechnest du durch die Formel:
berechnest du durch die Formel: