Punktsymmetrie – Definition, Erklärung und Beispiele
Punktsymmetrie tritt auf, wenn eine Figur sich nach einer halben Drehung um ihr Symmetriezentrum selbst abbildet. Entdecke, wie man punktsymmetrische Figuren erkennt, konstruiert und sogar bei Funktionsgraphen anwendet. Dies und mehr im folgenden Text!
Inhaltsverzeichnis zum Thema Punktsymmetrie
Punktsymmetrie im Überblick
Eine punktsymmetrische Figur wird durch eine halbe Drehung, also eine Drehung um
, auf sich selbst abgebildet.Durch eine Punktspiegelung entsteht eine punktsymmetrische Figur.
Die Punktsymmetrie zum Ursprung ist eine charakteristische Eigenschaft von Funktionsgraphen.
Quelle sofatutor.com
Wie willst du heute lernen?
Punktsymmetrie – Definition
Eine Punktsymmetrie liegt vor, wenn eine Figur durch eine halbe Drehung wieder auf sich selbst abgebildet wird. Der Punkt, um den diese Drehung erfolgt, ist das Symmetriezentrum der Punktsymmetrie.
Somit ist die Punktsymmetrie eine spezielle Form der Drehsymmetrie, bei der eine Drehung um exakt erforderlich ist.
Einfach erklärt bedeutet Punktsymmetrie bei einer Figur wie dieser Blume, dass sie nach einer halben Drehung exakt so aussieht wie zuvor.
Punktsymmetrie und Achsensymmetrie – Erklärung und Unterschiede
Die beiden häufigsten Formen von Symmetrie im Alltag sind Punktsymmetrie und Achsensymmetrie. Dabei können Figuren und Alltagsgegenstände nur eine oder auch beide Symmetriearten aufweisen. Eine Figur, die ein Symmetriezentrum besitzt, ist punktsymmetrisch und eine Figur, die zumindest eine Symmetrieachse aufweist, ist achsensymmetrisch. Dagegen nennen wir eine Figur, die keine Symmetrieeigenschaften besitzt, asymmetrisch.
Hier siehst du einige Objekte, die beide, eine oder keine Symmetrie aufweisen:
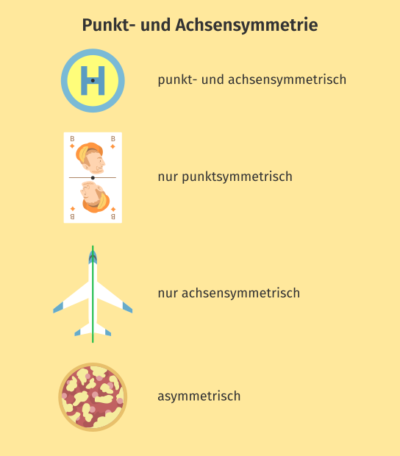
- Das Haltestellenschild hat mehrere Symmetrieachsen und ein Symmetriezentrum. Somit ist es sowohl achsen- als auch punktsymmetrisch.
- Die Spielkarte hat ein Symmetriezentrum, aber keine Symmetrieachse. Somit ist sie nur punktsymmetrisch.
- Das Flugzeug hat eine Symmetrieachse, aber kein Symmetriezentrum und ist daher nur achsensymmetrisch.
- Die Pizza besitzt aufgrund des unregelmäßigen Belags weder eine Symmetrieachse noch ein Symmetriezentrum. Sie ist also asymmetrisch.
Punktsymmetrische Figuren
Wir wollen uns nun genauer mit punktsymmetrischen Figuren beschäftigen. Dazu betrachten wir, wie wir punktsymmetrische Figuren zeichnen können und wie wir erkennen können, ob eine Figur punktsymmetrisch ist.
Punktsymmetrische Figuren zeichnen
Um eine Figur zu zeichnen, die Punktsymmetrie aufweist, nutzen wir die Punktspiegelung. Dadurch erzeugen wir die zweite Hälfte einer Figur, die punktsymmetrisch zur anderen Hälfte ist. Das Spiegelzentrum entspricht dann dem Symmetriezentrum der Figur. Die Konstruktion erfolgt für jeden Punkt in drei Schritten:
- Wir zeichnen einen Hilfskreis um das Spiegelzentrum
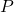, der durch einen Punkt der Ausgangsfigur geht. - Anschließend zeichnen wir eine Hilfsgerade durch den Punkt der Ausgangsfigur auf dem Hilfskreis und das Spiegelzentrum 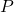, die den Kreis zweimal schneidet.
- Der Schnittpunkt von Hilfsgerade und Hilfskreis auf der gegenüberliegenden Seite des Spiegelzentrums ist der Bildpunkt.
Wenn wir diese Schritte für alle Punkte durchgeführt haben, verbinden wir die Bildpunkte wieder zu einer Figur. Ausgangsfigur und Bildfigur bilden dann zusammen eine punktsymmetrische Figur mit dem Spiegelzentrum als Symmetriezentrum.
Punktsymmetrische Figuren erkennen
Bei vielen Figuren lässt sich die Punktsymmetrie auf den ersten Blick vermuten. Du kannst auch versuchen, sie im Kopf um zu drehen, um zu sehen, ob das zu einer Veränderung führt. Wenn wir so eine vermeintliche Punktsymmetrie bei einer Figur erkennen, kann es gerade bei komplexeren Figuren sinnvoll sein, dies noch einmal zu überprüfen. Dazu zeichnest du Geraden durch das Symmetriezentrum und misst, ob die Abstände der markanten Punkte auf beiden Seiten übereinstimmen. Dies muss für alle Punkte einer Figur gelten, die punktsymmetrisch ist.
Bei einigen geometrischen Figuren können wir direkt sagen, ob diese punktsymmetrisch sind oder nicht. Hier sind die Eigenschaften von einigen speziellen Figuren zusammengefasst:
| Figur | Punktsymmetrie |
|---|---|
| Quadrat | punktsymmetrisch |
| Rechteck | punktsymmetrisch |
| Raute | punktsymmetrisch |
| Parallelogramm | punktsymmetrisch |
| Trapez | im Allgemeinen nicht punktsymmetrisch |
| Dreieck | nie punktsymmetrisch |
Punktsymmetrie bei Funktionsgraphen
Das Thema Punktsymmetrie spielt auch in der Kurvendiskussion von Funktionen eine Rolle. Dabei wird unter anderem untersucht, ob eine Punktsymmetrie des Graphen zum Ursprung vorliegt. Wir wollen im Folgenden betrachten, wie die Punktsymmetrie einer Funktion nachgewiesen werden kann und welche speziellen Kriterien dabei für ganzrationale Funktionen gelten.
Punktsymmetrie – Nachweis
Die Abbildung zeigt einen Funktionsgraphen, der punktsymmetrisch zum Ursprung verläuft. Durch die Betrachtung verschiedener Punkte können wir eine allgemeine Bedingung für die Punktsymmetrie vom Graphen ableiten. Dabei stellen wir fest, dass sich, wenn wir vom Ursprung als Symmetriezentrum aus gleichweit nach links und rechts gehen, der gleiche Funktionswert mit unterschiedlichem Vorzeichen ergibt:
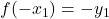
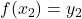und 
und 
Da dies für alle Punkte des Funktionsgraphen erfüllt sein muss, können wir eine Formel für die Punktsymmetrie formulieren:
Die Bedeutung der Punktsymmetrie bei Funktionsgraphen ist demnach, dass die Funktion für einen beliebigen 
-Wert (im Definitionsbereich) und den -Wert mit gleichem Betrag und umgekehrtem Vorzeichen Funktionswerte liefert, die den gleichen Betrag und entgegengesetzte Vorzeichen haben.
Hinweis: Es ist auch möglich, eine Punktsymmetrie zu einem beliebigen Punkt
im Koordinatensystem nachzuweisen. Dabei muss der Funktionsterm die Bedingung
für alle
Punktsymmetrie bei ganzrationalen Funktionen
Bei ganzrationalen Funktionen der Form 
kann die Punktsymmetrie des Graphen zum Ursprung auch direkt an den Exponenten, die der Funktionsterm enthält, abgelesen werden. Dabei gilt das folgende Kriterium:
Der Graph einer ganzrationalen Funktion verläuft punktsymmetrisch zum Ursprung, wenn der Funktionsterm nur ungerade Potenzen von
Dies gilt, da bei ungeraden Exponenten ein negatives Vorzeichen erhalten bleibt. So ist zum Beispiel 
. Daher erfüllt ein solcher Funktionsterm stets auch die Formel:
Beispiele für ganzrationale Funktionen:
Der Graph von 
ist punktsymmetrisch zum Ursprung, da er nur ungerade Potenzen, 
und 
, enthält.
Der Graph von 
ist nicht punktsymmetrisch zum Ursprung, da er die gerade Potenz 
enthält.
Der Graph von 
ist nicht punktsymmetrisch zum Ursprung, da er die Konstante 
enthält, die sich bezüglich des Vorzeichens, wie eine gerade Potenz, nicht verändert.
Hinweis: Der Graph von ist punktsymmetrisch zum Punkt 
. Dies können wir mit der Formel aus dem obigen Hinweis nachweisen:
Wir erhalten mit , 
und 
:
Häufig gestellte Fragen zum Thema Punktsymmetrie
Punktsymmetrie ist eine bestimmte Form der Symmetrie von Figuren.
Eine Figur, die punktsymmetrisch ist, wird durch eine halbe Drehung um das Symmetriezentrum wieder auf sich selbst abgebildet.
nicht verändert, alle Teile der Figur müssen entsprechend auf beiden Seiten des Symmetriezentrums vorhanden sein. um das Symmetriezentrum wieder auf sich selbst abgebildet wird.
für alle Werte aus dem Definitionsbereich erfüllt.Alle Parallelogramme, Rechtecke, Rauten und Quadrate sind punktsymmetrisch.
Eine Punktsymmetrie kann durch eine Punktspiegelung am Symmetriezentrum nachgewiesen oder erzeugt werden.
Bei einer Achsensymmetrie ist eine Figur symmetrisch zu einer Symmetrieachse, während bei einer Punktsymmetrie eine Symmetrie zu einem Punkt, dem sogenannten Symmetriezentrum, vorliegt.
Eine punktsymmetrische Figur kann auch achsensymmetrisch sein. Es gibt aber auch Figuren, die nur punkt- und nicht achsensymmetrisch sind.
Eine Gerade ist punktsymmetrisch, solange das Symmetriezentrum ein Punkt auf der Geraden ist.
Bei zwei Geraden unterscheiden wir zwei Fälle:
- Schneiden sich die Geraden, sind sie punktsymmetrisch zu ihrem Schnittpunkt.
- Verlaufen die Geraden parallel, sind sie punktsymmetrisch zu einem beliebigen Punkt auf einer Geraden, die genau in der Mitte parallel zu beiden Geraden verläuft.
Alle Artikel aus dem Fach Mathematik