Quadratische Funktionen – Erklärung
In der Mathematik sindquadratische FunktionenFunktionen, deren höchste Potenzdas Quadratist. Ihre Graphen bildenParabelnund können durch Verschiebung, Streckung, Stauchung und Spiegelung variieren. Erfahre mehr über Funktionsgleichungen, Nullstellenberechnung und Zeichnen von Parabeln. Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Quadratische Funktionen
Quadratische Funktionen – Definition
Quadratische Funktionen sind Funktionen, in denen die höchste Potenz von ![]() das Quadrat ist. Der Graph einer quadratischen Funktion ist immer eine Parabel, verläuft also in einer Art U-Form.
das Quadrat ist. Der Graph einer quadratischen Funktion ist immer eine Parabel, verläuft also in einer Art U-Form.
Der Definitionsbereich ![]() einer quadratischen Funktion umfasst alle
einer quadratischen Funktion umfasst alle ![]() -Werte, für die der Funktionsterm definiert ist. In der Regel gilt für quadratische Funktionen:
-Werte, für die der Funktionsterm definiert ist. In der Regel gilt für quadratische Funktionen:
![]()
Der Wertebereich ![]() einer quadratischen Funktion umfasst alle
einer quadratischen Funktion umfasst alle ![]() -Werte, die die Funktion annehmen kann. Durch den Verlauf der Parabel mit einem höchsten oder tiefsten Punkt im Scheitel ist die Wertemenge begrenzt.
-Werte, die die Funktion annehmen kann. Durch den Verlauf der Parabel mit einem höchsten oder tiefsten Punkt im Scheitel ist die Wertemenge begrenzt.
Quadratische Funktionen – Funktionsgleichung
Die Funktionsgleichung quadratischer Funktionen kann in verschiedenen Formen dargestellt werden. Wir gehen im Folgenden genauer auf die allgemeine Form, die Normalform und die Scheitelpunktform ein.
Quadratische Funktionen – allgemeine Form
Die allgemeine Form der Funktionsgleichung einer quadratischen Funktion lautet:
![]()
Die einzelnen Glieder der Gleichung nennen wir:
 : das quadratische Glied
: das quadratische Glied : das lineare Glied
: das lineare Glied : das absolute Glied
: das absolute Glied
Der Parameter ![]() darf nicht
darf nicht ![]() sein, da in der Gleichung ansonsten kein
sein, da in der Gleichung ansonsten kein ![]() mehr vorkommen würde und es sich somit nur noch um eine lineare Funktion und nicht um eine quadratische Funktion handeln würde.
mehr vorkommen würde und es sich somit nur noch um eine lineare Funktion und nicht um eine quadratische Funktion handeln würde.
Hinweis: Anstelle von ![]() kann für den Funktionswert auch
kann für den Funktionswert auch ![]() stehen.
stehen.
Quadratische Funktion – Normalform:
Die Normalform ist ein Spezialfall der allgemeinen Form. Bei der Normalform ist der Koeffizient des Terms ![]() normiert. Das bedeutet, der Koeffizient vor
normiert. Das bedeutet, der Koeffizient vor ![]() ist
ist ![]() . Ist
. Ist ![]() , kann es in der Funktionsgleichung weggelassen werden.
, kann es in der Funktionsgleichung weggelassen werden.
Liegt eine Parabel in Normalform vor, werden anstelle der Parameter ![]() und
und ![]() manchmal auch
manchmal auch ![]() und
und ![]() verwendet:
verwendet:
![]()
Quadratische Funktionen – Scheitelpunktform
Aus der Scheitelpunktform lässt sich der Scheitelpunkt einer quadratischen Funktion direkt ablesen. Als Scheitelpunkt wird der höchste oder tiefste Punkt des Graphen bezeichnet. Die Scheitelpunktform lautet:
![]()
Der Scheitelpunkt ![]() einer quadratischen Funktion liegt bei
einer quadratischen Funktion liegt bei ![]() .
.
Allgemeine und Scheitelpunktform lassen sich ineinander umwandeln. Wie das funktioniert, wird im Abschnitt Funktionsterm umformen erklärt.
Quadratische Funktionen – Parabeln
Der Graph einer quadratischen Funktion ist immer eine Parabel.
Betrachten wir zunächst die sogenannte Normalparabel. Als Normalparabel wird der Graph der quadratischen Funktion ![]() bezeichnet.
bezeichnet.

Quelle sofatutor.com
Der Scheitelpunkt der Normalparabel liegt bei ![]() . Als Scheitelpunkt wird der tiefste oder höchste Punkt der Parabel bezeichnet, es ist also der Punkt, an dem die Parabel ihre Richtung ändert. Die Normalparabel besitzt einen Tiefpunkt. Durch den Einfluss verschiedener Parameter kann sich der Verlauf der Normalparabel ändern. Dabei gibt es folgende Möglichkeiten:
. Als Scheitelpunkt wird der tiefste oder höchste Punkt der Parabel bezeichnet, es ist also der Punkt, an dem die Parabel ihre Richtung ändert. Die Normalparabel besitzt einen Tiefpunkt. Durch den Einfluss verschiedener Parameter kann sich der Verlauf der Normalparabel ändern. Dabei gibt es folgende Möglichkeiten:
- Verschiebung des Scheitelpunkts in Richtung der
 -Achse (nach rechts oder links)
-Achse (nach rechts oder links) - Verschiebung des Scheitelpunkts in Richtung der
 -Achse (nach oben oder unten)
-Achse (nach oben oder unten) - Streckung (schmalerer Verlauf) oder Stauchung (breiterer Verlauf)
- Spiegelung an der
 -Achse
-Achse
Jede Parabel besitzt eine Symmetrieachse, die parallel zur ![]() -Achse verläuft und die Parabel in ihrem Scheitelpunkt schneidet. Bei der Normalparabel stellt die
-Achse verläuft und die Parabel in ihrem Scheitelpunkt schneidet. Bei der Normalparabel stellt die ![]() -Achse selbst die Symmetrieachse dar.
-Achse selbst die Symmetrieachse dar.
Den Einfluss der Parameter auf den Verlauf der quadratischen Funktion schauen wir uns in den folgenden Abschnitten genauer an.
Quadratische Funktion – Verschiebung in ![]() -Richtung
-Richtung
Betrachten wir dafür die folgenden quadratischen Funktionen:
![]()
![]()
Eingetragen in das Koordinatensystem sehen wir, dass die Graphen der Funktionen wie die Normalparabel verlaufen, allerdings um eine Einheit nach links (![]() ) beziehungsweise eine Einheit nach rechts (
) beziehungsweise eine Einheit nach rechts (![]() ) verschoben.
) verschoben.

Der Scheitelpunkt von ![]() liegt somit bei
liegt somit bei ![]() und der von
und der von ![]() bei
bei ![]() . Beide Funktionen gehören zur Form
. Beide Funktionen gehören zur Form ![]() . Wir können daraus ableiten:
. Wir können daraus ableiten:
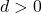 : Parabel ist um
: Parabel ist um 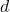 Einheiten nach links verschoben.
Einheiten nach links verschoben. : Parabel ist um
: Parabel ist um 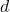 Einheiten nach rechts verschoben.
Einheiten nach rechts verschoben.
Beachte: Die Verschiebung der Parabel in ![]() -Richtung erfolgt mit entgegengesetztem Vorzeichen.
-Richtung erfolgt mit entgegengesetztem Vorzeichen.
Quadratische Funktionen – Verschiebung in ![]() -Richtung
-Richtung
Die Verschiebung in ![]() -Richtung wird durch den Parameter
-Richtung wird durch den Parameter ![]() beeinflusst. Parabeln von Funktionen der Form
beeinflusst. Parabeln von Funktionen der Form ![]() sind in Richtung der
sind in Richtung der ![]() -Achse verschoben. Dabei gilt:
-Achse verschoben. Dabei gilt:
 : Parabel ist um
: Parabel ist um  Einheiten nach oben verschoben.
Einheiten nach oben verschoben. : Parabel ist um
: Parabel ist um  Einheiten nach unten verschoben.
Einheiten nach unten verschoben.
Beispiel:
Im Vergleich zur Normalparabel ![]() (blau) ist der Graph von
(blau) ist der Graph von ![]() eine Einheit nach oben verschoben (grün). Der Graph von
eine Einheit nach oben verschoben (grün). Der Graph von ![]() ist dagegen wegen
ist dagegen wegen ![]() um zwei Einheiten nach unten verschoben (gelb).
um zwei Einheiten nach unten verschoben (gelb).

Quadratische Funktionen – Streckung und Stauchung
Für die Streckung und Stauchung einer Funktion ist der Parameter ![]() verantwortlich, der als Koeffizient vor
verantwortlich, der als Koeffizient vor ![]() steht. Dabei gilt:
steht. Dabei gilt:
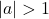 : Parabel ist gestreckt, d. h., der Graph ist schmaler.
: Parabel ist gestreckt, d. h., der Graph ist schmaler.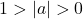 : Parabel ist gestaucht, d. h., der Graph ist breiter.
: Parabel ist gestaucht, d. h., der Graph ist breiter.
In der Normalparabel ist ![]() und wird daher in der Funktionsgleichung häufig weggelassen. Die Normalparabel ist somit weder gestreckt noch gestaucht.
und wird daher in der Funktionsgleichung häufig weggelassen. Die Normalparabel ist somit weder gestreckt noch gestaucht.

In der Grafik sehen wir: Je größer ![]() ist, desto schlanker ist die Parabel.
ist, desto schlanker ist die Parabel.
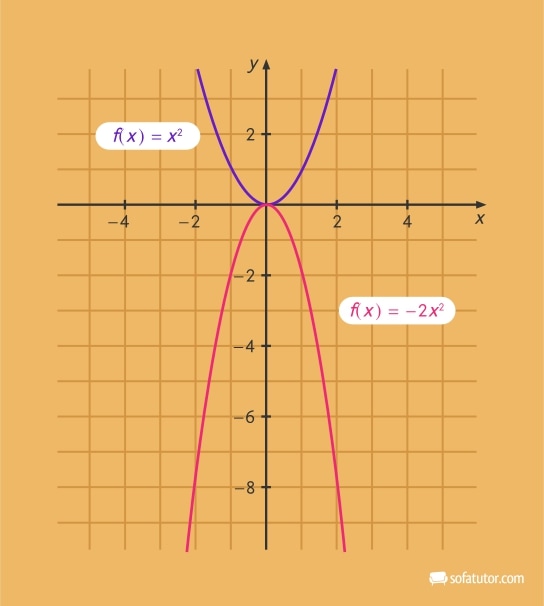
Quadratische Funktionen – Spiegelung an der ![]() -Achse
-Achse
Auch für die Spiegelung an der ![]() -Achse ist der Parameter
-Achse ist der Parameter ![]() verantwortlich. Ist
verantwortlich. Ist ![]() negativ, wird die Parabel an der
negativ, wird die Parabel an der ![]() -Achse gespiegelt und ist nach unten geöffnet. Dabei gilt:
-Achse gespiegelt und ist nach unten geöffnet. Dabei gilt:
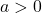 : Die Parabel ist nach oben geöffnet.
: Die Parabel ist nach oben geöffnet.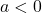 : Die Parabel ist nach unten geöffnet.
: Die Parabel ist nach unten geöffnet.
In der folgenden Grafik ist zu erkennen, dass der Funktionsgraph mit einem negativen ![]() nach unten geöffnet ist. Da
nach unten geöffnet ist. Da ![]() kleiner als
kleiner als ![]() ist, ist der Graph der Funktion zusätzlich auch gestreckt, er ist also schmaler.
ist, ist der Graph der Funktion zusätzlich auch gestreckt, er ist also schmaler.
Ist die Parabel nach oben geöffnet (![]() ), ist der Scheitelpunkt der tiefste Punkt (Tiefpunkt) der Parabel. Ist die Parabel nach unten geöffnet (
), ist der Scheitelpunkt der tiefste Punkt (Tiefpunkt) der Parabel. Ist die Parabel nach unten geöffnet (![]() ), ist der Scheitelpunkt der höchste Punkt (Hochpunkt) der Parabel.
), ist der Scheitelpunkt der höchste Punkt (Hochpunkt) der Parabel.
Quadratische Funktionen – Verlauf erkennen
Anhand der Funktionsgleichung können somit schon wichtige Eigenschaften der Parabel abgelesen werden. Betrachten wir dafür die folgende quadratische Funktion:
![]()
Die Parabel dieser Funktion verhält sich im Vergleich zur Normalparabel folgendermaßen:
 nach unten geöffnet und gestreckt
nach unten geöffnet und gestreckt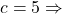 um
um 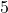 Einheiten nach oben verschoben
Einheiten nach oben verschoben um
um 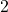 Einheiten nach links verschoben
Einheiten nach links verschoben
Quadratische Funktionen – Nullstellen berechnen
Als Nullstellen werden die Punkte bezeichnet, an denen der Graph einer Funktion die ![]() -Achse schneidet. Nullstellen sind also die
-Achse schneidet. Nullstellen sind also die ![]() -Werte, für die der Funktionswert gleich null ist (
-Werte, für die der Funktionswert gleich null ist (![]() ). Eine Parabel kann zwei, eine oder keine Nullstellen besitzen.
). Eine Parabel kann zwei, eine oder keine Nullstellen besitzen.
Die Formel zur Berechnung der Nullstellen einer quadratischen Funktion hängt von der Form ab, in der die quadratische Funktion gegeben ist.
Nullstellen bestimmen – allgemeine Form
Ist eine quadratische Funktion in der allgemeinen Form ![]() gegeben, werden die Nullstellen mit der Mitternachtsformel berechnet. Diese lautet:
gegeben, werden die Nullstellen mit der Mitternachtsformel berechnet. Diese lautet:
![]()
Die Parameter aus der Funktionsgleichung werden in die Mitternachtsformel eingesetzt. Aufgrund des Plusminuszeichens (![]() ) müssen die Werte getrennt berechnet werden.
) müssen die Werte getrennt berechnet werden.
Die Anzahl der Nullstellen hängt dabei von dem Term ab, der unter der Wurzel steht. Er wird auch Diskriminante ![]() genannt. Es gilt:
genannt. Es gilt:
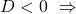 keine Lösung
keine Lösung eine Lösung
eine Lösung zwei Lösungen
zwei Lösungen
Beispiel:
Betrachten wir die quadratische Funktion ![]() .
.
Zunächst setzen wir die Parameter ![]() ,
, ![]() und
und ![]() in die Mitternachtsformel ein und vereinfachen diese.
in die Mitternachtsformel ein und vereinfachen diese.
![]()
Nun trennen wir den Term und erhalten für die beiden Nullstellen:
![]()
![]()
Die beiden Nullstellen dieser quadratischen Funktion liegen bei ![]() und
und ![]() .
.
Nullstellen bestimmen – Normalform
Ist eine quadratische Funktion in der Normalform ![]() gegeben, werden die Nullstellen mit der
gegeben, werden die Nullstellen mit der ![]() –Formel berechnet. Diese lautet:
–Formel berechnet. Diese lautet:
![]()
Auch in der ![]() -Formel kommt ein Plusminuszeichen vor, weshalb es zwei mögliche Lösungen gibt. Wie in der Mitternachtsformel ist der Term unter der Wurzel maßgeblich für die Anzahl der Lösungen.
-Formel kommt ein Plusminuszeichen vor, weshalb es zwei mögliche Lösungen gibt. Wie in der Mitternachtsformel ist der Term unter der Wurzel maßgeblich für die Anzahl der Lösungen.
Die Parameter ![]() und
und ![]() werden in die Formel eingesetzt, diese wird vereinfacht und
werden in die Formel eingesetzt, diese wird vereinfacht und ![]() und
und ![]() können durch eine Trennung der Terme berechnet werden.
können durch eine Trennung der Terme berechnet werden.
Nullstellen bestimmen – Scheitelpunktform
Ist eine quadratische Funktion in der Scheitelpunktform ![]() gegeben, muss die Formel lediglich gleich
gegeben, muss die Formel lediglich gleich ![]() gesetzt und nach
gesetzt und nach ![]() umgestellt werden.
umgestellt werden.

Die Lösungsformel für die Scheitelpunktform lautet demnach:
![]()
Auch hier müssen die Parameter ![]() ,
, ![]() und
und ![]() eingesetzt, die Terme in einen Plus- und einen Minusterm aufgeteilt und die Werte für
eingesetzt, die Terme in einen Plus- und einen Minusterm aufgeteilt und die Werte für ![]() und
und ![]() berechnet werden.
berechnet werden.
Beispiel:
![]()
![]()
![]()
![]()
![]()
Die Nullstellen dieser quadratischen Gleichung liegen bei ![]() und
und ![]() .
.
Quadratische Funktionen – Funktionsgleichung bestimmen
Um die Funktionsgleichung einer quadratischen Funktion anhand ihrer Parabel zu bestimmen, benötigen wir drei Punkte, die auf der Parabel liegen. Zur Bestimmung der Funktionsgleichung gehen wir dann folgendermaßen vor:
- Die Koordinaten dreier Punkte, die auf der Parabel liegen, ablesen
- Die Koordinaten jeweils in die allgemeine Form der Funktionsgleichung einsetzen, um drei Gleichungen zu erhalten
- Gleichungssystem aufstellen
- Die Parameter
 ,
, 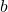 und
und  über das Gleichungssystem bestimmen
über das Gleichungssystem bestimmen  ,
, 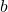 und
und  in die Funktionsgleichung einsetzen
in die Funktionsgleichung einsetzen
Beispiel:
Betrachten wir die folgende Parabel:

Zunächst wählen wir drei Punkte, die auf der Parabel liegen.
![]()
![]()
![]()
Setzen wir die drei Punkte jeweils in die Funktionsgleichung ein, erhalten wir die drei Gleichungen:

Aus der ersten Gleichung können wir ![]() direkt ablesen. Diesen Wert setzen wir in die anderen beiden Gleichungen ein, sodass wir im nächsten Schritt nur noch
direkt ablesen. Diesen Wert setzen wir in die anderen beiden Gleichungen ein, sodass wir im nächsten Schritt nur noch ![]() und
und ![]() bestimmen müssen.
bestimmen müssen.
Wir stellen folgendes Gleichungssystem auf:
![]()
Um das Gleichungssystem zu lösen, stellen wir eine Gleichung nach einer Variablen um und setzen sie dann in die zweite Gleichung ein.
Stellen wir dafür die erste Gleichung nach ![]() um:
um:
![]()
Setzen wir das in die zweite Gleichung ein und stellen diese nach ![]() um, erhalten wir:
um, erhalten wir:
![]()
![]()
Nun können wir ![]() in die Gleichung
in die Gleichung ![]() einsetzen und erhalten:
einsetzen und erhalten:
![]()
![]()
Die Funktionsgleichung der quadratischen Funktion lautet:
![]()
Hinweis: Das hier beschriebene Verfahren funktioniert für drei beliebige Punkte, die auf dem Graphen einer quadratischen Funktion liegen. Bei geeigneten Angaben wie z. B. dem Scheitelpunkt oder den Nullstellen der Parabel kann ein Ansatz mit der Scheitelpunktform (![]() ) oder in der Nullstellenform (
) oder in der Nullstellenform (![]() ) schneller zum Ziel führen.
) schneller zum Ziel führen.
Quadratische Funktionen zeichnen
Beim Zeichnen quadratischer Funktionen sind Wertetabellen hilfreich. Dabei suchst du dir verschiedene Zahlen für ![]() , setzt diese in die Funktionsgleichung ein und ermittelst die dazugehörigen
, setzt diese in die Funktionsgleichung ein und ermittelst die dazugehörigen ![]() -Werte. Die Wertepaare werden im Anschluss in einem Koordinatensystem abgetragen und zur Parabel verbunden. Dabei ist es wichtig, möglichst genau zu arbeiten, indem möglichst viele Punkte berechnet werden.
-Werte. Die Wertepaare werden im Anschluss in einem Koordinatensystem abgetragen und zur Parabel verbunden. Dabei ist es wichtig, möglichst genau zu arbeiten, indem möglichst viele Punkte berechnet werden.
Zudem können anhand der Parameter schon Eigenschaften der Parabel abgeleitet werden.
Beispiel
Betrachten wir die quadratische Funktion ![]() .
.
Folgende Eigenschaften der Parabel der quadratischen Funktion lassen sich bereits aus der Funktionsgleichung ablesen:
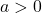 : nach oben geöffnet
: nach oben geöffnet : gestaucht
: gestaucht : nach unten verschoben
: nach unten verschoben
Nun können wir eine Wertetabelle für diese quadratische Funktion erstellen, um Punkte zu ermitteln, die auf der Parabel liegen. Dafür wählen wir uns Werte für ![]() , setzen diese in die Funktionsgleichung ein und berechnen den dazugehörigen
, setzen diese in die Funktionsgleichung ein und berechnen den dazugehörigen ![]() -Wert.
-Wert.
![]() :
: ![]()
Alle Wertepaare können wir in die Wertetabelle eintragen.
| x-Wert | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
Diese Punkte können nun im Koordinatensystem eingezeichnet und zur Parabel verbunden werden.

Betrachten wir noch die Parabel ![]() . Hier lassen sich die folgenden Eigenschaften aus der Funktionsgleichung ablesen:
. Hier lassen sich die folgenden Eigenschaften aus der Funktionsgleichung ablesen:
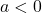 : nach unten geöffnet
: nach unten geöffnet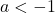 : gestreckt
: gestreckt : nach oben verschoben
: nach oben verschoben
Auch für diese Funktionsgleichung können wir eine Wertetabelle anfertigen und die Parabel der quadratischen Funktion einzeichnen.
| x-Werte | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
Quadratische Funktionen – Funktionsterm umformen
Die Scheitelpunktform und die allgemeine Form sind lediglich verschiedene Schreibweisen der Funktionsgleichung und lassen sich ineinander überführen. Um die allgemeine Form in die Scheitelpunktform umzuwandeln, nutzen wir die quadratische Ergänzung. Wollen wir die Scheitelpunktform in die allgemeine Form bringen, dann wenden wir die binomischen Formeln<span style=“font-weight: 400;“> an.

Beispiel:
![]() (allgemeine Form)
(allgemeine Form)
![]() (Scheitelpunktform)
(Scheitelpunktform)
In den folgenden Abschnitten wandeln wir diese beiden Formen ineinander um.
Quadratische Funktionen – Scheitelpunktform in allgemeine Form umwandeln
In der Scheitelpunktform haben wir eine Klammer, die quadriert wird. Dafür wenden wir die binomischen Formeln an. Eine Hilfsklammer um die binomische Formel kann dir helfen, die einzelnen Rechenschritte nicht zu vermischen. Wir wenden zunächst innerhalb der Hilfsklammer die erste binomische Formel an:
![]()
![]()
Die Hilfsklammer können wir nun auflösen, indem alle drei Summanden mit dem Faktor vor der Klammer (![]() ) multipliziert werden.
) multipliziert werden.
![]()
![]()
Fassen wir das noch zusammen, erhalten wir die allgemeine Form dieser quadratischen Funktion:
![]()
![]()
Die wichtigsten Schritte bei dieser Umwandlung sind:
- Hilfsklammer setzen,
- binomische Formel anwenden,
- Hilfsklammer auflösen und
- zusammenfassen.
Quadratische Funktionen – allgemeine Form in Scheitelpunktform umwandeln
Bei dieser Umformung wenden wir die quadratische Ergänzung an. Dafür klammern wir zunächst den Faktor (![]() ) aus, der vor
) aus, der vor ![]() steht. Dabei muss auch auf die Vorzeichen geachtet werden.
steht. Dabei muss auch auf die Vorzeichen geachtet werden.
![]()
![]()
Betrachten wir jetzt die Klammer, erinnert diese schon etwas an die erste binomische Formel. Nun wenden wir die quadratische Ergänzung an. Dafür addieren wir ![]() (in diesem Fall
(in diesem Fall ![]() ) und ziehen es gleich wieder ab. Nun können wir die ersten Summanden zur ersten binomischen Formel zusammenfassen.
) und ziehen es gleich wieder ab. Nun können wir die ersten Summanden zur ersten binomischen Formel zusammenfassen.
![]()
![]()
Im nächsten Schritt lösen wir die äußere Klammer auf und fassen zusammen.
![]()
![]()
Die wichtigsten Schritte bei dieser Umwandlung sind:
- Faktor vor
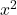 ausklammern,
ausklammern, - quadratische Ergänzung durchführen,
- binomische Formel anwenden,
- äußere Klammer auflösen und
- zusammenfassen.
Quadratische Funktionen – Aufgaben und Beispiele
Aufgabe 1: quadratische Funktion verschieben
Gegeben ist die Normalparabel ![]() . Die Parabel wird nun um
. Die Parabel wird nun um ![]() Einheiten nach oben und
Einheiten nach oben und ![]() Einheiten nach rechts verschoben. Wie ändert sich die Funktionsgleichung?
Einheiten nach rechts verschoben. Wie ändert sich die Funktionsgleichung?
Lösung Aufgabe 1:
Eine Verschiebung nach oben oder unten wird immer durch den Parameter ![]() angegeben. Ist die Parabel nach oben verschoben, ist
angegeben. Ist die Parabel nach oben verschoben, ist ![]() positiv. In diesem Fall muss also der Parameter
positiv. In diesem Fall muss also der Parameter ![]() ergänzt werden.
ergänzt werden.
Die Verschiebung nach rechts und links wird durch den Parameter ![]() angegeben. Bei einer Verschiebung nach rechts ist
angegeben. Bei einer Verschiebung nach rechts ist ![]() negativ. Demnach muss in der Funktionsgleichung der Parameter
negativ. Demnach muss in der Funktionsgleichung der Parameter ![]() ergänzt werden.
ergänzt werden.
Die Funktionsgleichung lautet:
![]()
Aufgabe 2: Funktionsgleichung umwandeln
Es ist eine Funktionsgleichung in allgemeiner Form gegeben: ![]() . Wandle diese in die Scheitelpunktform um.
. Wandle diese in die Scheitelpunktform um.
Lösung Aufgabe 2:
Mithilfe der quadratischen Ergänzung können wir die allgemeine Form in die Scheitelpunktform umwandeln.

Die Scheitelpunktform lautet:
![]()
Aufgabe 3: Nullstellenberechnung quadratischer Funktionen
Berechne die Nullstellen der folgenden Funktionen:
![]()
![]()
Lösung Aufgabe 3:
Zunächst muss die Form, in der die quadratische Funktion gegeben ist, bestimmt werden:
![]() : Normalform
: Normalform
![]() : Scheitelpunktform
: Scheitelpunktform
Nun können die Nullstellen mit den entsprechenden Formeln berechnet werden.
Beginnen wir mit ![]() . Dafür nutzen wir die
. Dafür nutzen wir die ![]() -Formel:
-Formel:
![]()
![]()
![]()

![]()
![]()
Die quadratische Funktion ![]() besitzt Nullstellen bei
besitzt Nullstellen bei ![]() und
und ![]() .
.
Für die quadratische Funktion ![]() , die in der Scheitelpunktform gegeben ist, nutzen wir die folgende Formel zur Berechnung der Nullstellen:
, die in der Scheitelpunktform gegeben ist, nutzen wir die folgende Formel zur Berechnung der Nullstellen:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Die quadratische Funktion ![]() besitzt Nullstellen bei
besitzt Nullstellen bei ![]() und
und ![]() .
.
Häufig gestellte Fragen zum Thema Quadratische Funktionen

