Koordinatensystem – Aufbau, Erklärung und Beispiele
Punkte und Figuren darstellen! Ein Koordinatensystem ermöglicht die Darstellung von Punkten in Quadranten. Lerne den Aufbau und die Notation von Koordinaten und entdecke, wie Punkte eingetragen und abgelesen werden. Interessiert? Dies und mehr im folgenden Text!
Inhaltsverzeichnis zum Thema Koordinatensystem
Koordinatensystem – Einführung
In einem Koordinatensystem, auch kurz KOS oder KoSy, können Punkte und andere geometrische Objekte, wie Geraden, dargestellt werden. Einzelne Zahlen können wir auf einem Zahlenstrahl darstellen, auf dem Abstände zwischen zwei benachbarten Zahlen immer gleich groß sind.

Quelle sofatutor.com
Ein Zahlenstrahl veranschaulicht so einzelne Zahlen, es ist aber nicht möglich, ein Zahlenpaar darzustellen. Dazu wird zum Beispiel ein zweiter Zahlenstrahl für die zweite Zahl benötigt. Wenn wir mehrere Zahlen, auch Koordinaten, gleichzeitig darstellen können, sprechen wir von einem Koordinatensystem.
Das am häufigsten verwendete Koordinatensystem in Mathe ist das kartesische Koordinatensystem, bei dem ein zweiter Zahlenstrahl senkrecht zum ersten steht.
Im Folgenden wollen wir das zweidimensionale kartesische Koordinatensystem genauer betrachten.
Aufbau eines Koordinatensystems
Das zweidimensionale kartesische Koordinatensystem besteht aus einer ![]() -Achse, die horizontal verläuft, und einer dazu orthogonalen, vertikalen
-Achse, die horizontal verläuft, und einer dazu orthogonalen, vertikalen ![]() -Achse. Beide Achsen sehen dabei aus wie ein Zahlenstrahl. Der Pfeil der
-Achse. Beide Achsen sehen dabei aus wie ein Zahlenstrahl. Der Pfeil der ![]() -Achse zeigt nach rechts, der Pfeil der
-Achse zeigt nach rechts, der Pfeil der ![]() -Achse nach oben, jeweils in die Richtung steigender Werte. Folgendes Bild zeigt ein kartesisches Koordinatensystem:
-Achse nach oben, jeweils in die Richtung steigender Werte. Folgendes Bild zeigt ein kartesisches Koordinatensystem:

Der Schnittpunkt der beiden Achsen ist der Punkt ![]() . Er heißt Koordinatenursprung, oder kurz Ursprung.
. Er heißt Koordinatenursprung, oder kurz Ursprung.
Die ![]() -Achse wird auch Abszisse oder Rechtsachse genannt, die
-Achse wird auch Abszisse oder Rechtsachse genannt, die ![]() -Achse auch Ordinate oder Hochachse.
-Achse auch Ordinate oder Hochachse.
Wenn ein Koordinatensystem erstellt wird, darf nie die Beschriftung der Achsen vergessen werden. Wie bei einem Zahlenstrahl müssen auch hier kleine Striche in regelmäßigen Abständen gemacht und die entsprechenden Zahlen daran geschrieben werden.
Hinweis: Ein dreidimensionales kartesisches Koordinatensystem hat zusätzlich eine ![]() -Achse, die aus der Ebene heraus gezeichnet wird.
-Achse, die aus der Ebene heraus gezeichnet wird.
Die Quadranten im Koordinatensystem
Das Koordinatensystem ist in vier Quadranten unterteilt. Die Unterteilung erfolgt entlang der Koordinatenachsen.
Die Quadranten werden in der Regel, beginnend mit dem ersten Quadranten oben rechts, gegen den Uhrzeigersinn mit römischen Zahlen nummeriert. Die Position der einzelnen Quadranten siehst du hier:

Wir sehen auch, dass die Vorzeichen der Koordinaten sich in den Quadranten unterscheiden. Es gilt:
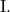 Quadrant:
Quadrant:  und
und 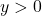
 Quadrant:
Quadrant:  und
und 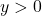
 Quadrant:
Quadrant:  und
und 
 Quadrant:
Quadrant:  und
und 
Hinweis: Die Punkte auf den Koordinatenachsen werden keinem Quadranten zugeordnet, da hier eine der Koordinaten den Wert ![]() hat.
hat.
Punkte in ein Koordinatensystem eintragen und ablesen
Die Lage von Punkten im Koordinatensystem wird durch die folgende Notation eindeutig beschrieben:
![]()
Der Punkt ist ein Zahlenpaar, bestehend aus zwei Koordinaten:
- Die erste Zahl steht für die
 -Koordinate des Punkts.
-Koordinate des Punkts. - Die zweite Zahl steht für die
 -Koordinate des Punkts.
-Koordinate des Punkts.
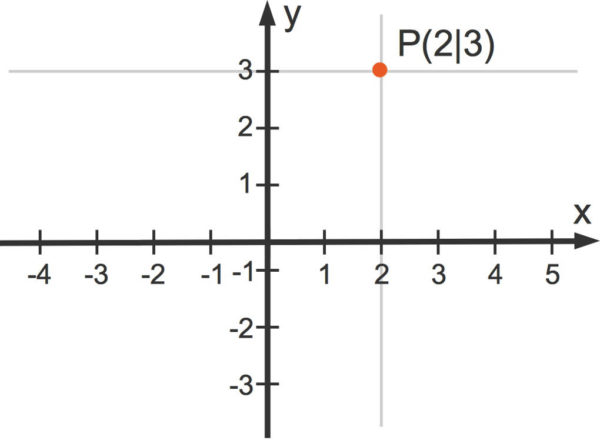
Beispiel: ![]()
Dies bedeutet, der Punkt ![]() hat die
hat die ![]() -Koordinate
-Koordinate ![]() und
und ![]() -Koordinate
-Koordinate ![]() . Damit liegt er im
. Damit liegt er im ![]() Quadranten rechts oben, da beide Koordinaten positiv sind.
Quadranten rechts oben, da beide Koordinaten positiv sind.
Punkt eintragen
Nun wollen wir diesen Punkt in ein Koordinatensystem eintragen. Dazu wird erst ein rechtwinkliges Koordinatensystem mit einer waagerechten ![]() -Achse und einer senkrechten
-Achse und einer senkrechten ![]() -Achse gezeichnet und beschriftet.
-Achse gezeichnet und beschriftet.
- Wir suchen
 auf der
auf der  -Achse und zeichnen durch diese Stelle eine zur
-Achse und zeichnen durch diese Stelle eine zur  -Achse parallele Gerade ein. Alle Punkte auf dieser Gerade haben den
-Achse parallele Gerade ein. Alle Punkte auf dieser Gerade haben den  -Wert
-Wert 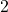 .
. - Dann zeichnen wir analog durch
 auf der
auf der  -Achse eine zur
-Achse eine zur 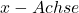 parallele Gerade ein.
parallele Gerade ein. - Diese beiden Geraden schneiden sich im Punkt
 , den wir mit Farbe oder einem Kreuz markieren.
, den wir mit Farbe oder einem Kreuz markieren.
Punkt ablesen
Ist ein Punkt im Koordinatensystem eingetragen, können die Koordinaten abgelesen werden.
- Die
 -Koordinate entspricht dem
-Koordinate entspricht dem  -Wert, bei dem eine zur
-Wert, bei dem eine zur  -Achse parallele Gerade durch den Punkt die
-Achse parallele Gerade durch den Punkt die  -Achse schneidet.
-Achse schneidet. - Analog ist die
 -Koordinate des Punkts gleich dem
-Koordinate des Punkts gleich dem  -Wert, bei dem eine zur
-Wert, bei dem eine zur  -Achse parallele Gerade durch den Punkt die
-Achse parallele Gerade durch den Punkt die  -Achse schneidet.
-Achse schneidet.
Schauen wir uns dazu folgendes Beispiel an. Die Koordinaten des grünen Punkts sollen ermittelt werden:
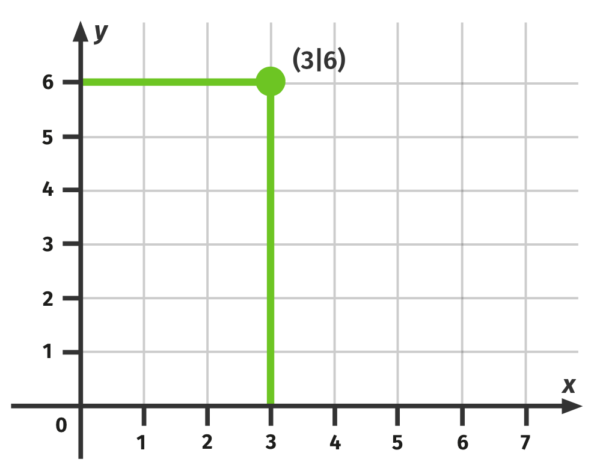
Wir können für den ![]() -Wert die
-Wert die ![]() und für den
und für den ![]() -Wert die Zahl
-Wert die Zahl ![]() ablesen. Der Punkt liegt also bei:
ablesen. Der Punkt liegt also bei:
![]()
Hinweis: Das Einzeichnen der Geraden ist zum Einzeichnen und Ablesen von Punkten nicht zwingend erforderlich. Du kannst dich zum Beispiel auch an den Kästchen in deinem Heft orientieren oder ein Lineal oder Geodreieck anlegen.
Häufig gestellte Fragen zum Thema Koordinatensystem









