Kettenregel – Formel, Herleitung und Beispiele
Die Kettenregel ist eine wichtige Regel in der Differenzialrechnung für verkettete Funktionen. Lerne, wie sie die Ableitung von verketteten Funktionen bestimmt und wie sie in der Mathematik angewendet wird. Interessiert? Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Kettenregel
Kettenregel einfach erklärt
Die Kettenregel ist in der Mathematik eine wichtige Regel in der Differenzialrechnung. Sie dient zur Bestimmung der Ableitung von verketteten Funktionen. Die Kettenregel wird also bei der Kurvendiskussion von verketteten Funktionen benötigt.
Verkettete Funktion:
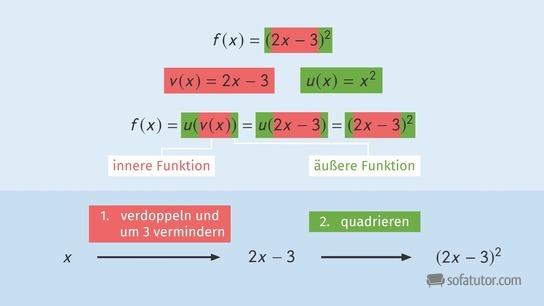
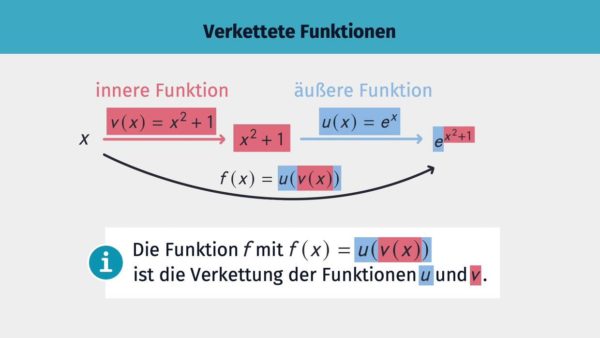
Bei einer verketteten Funktion werden zwei (oder mehr) Funktionsvorschriften hintereinander ausgeführt. Dabei wird die zuerst angewandte Funktion als innere Funktion ![]() bezeichnet, die zuletzt ausgeführte Funktion heißt äußere Funktion
bezeichnet, die zuletzt ausgeführte Funktion heißt äußere Funktion ![]() . Für die verkettete Funktion
. Für die verkettete Funktion ![]() schreiben wir dann:
schreiben wir dann:
![]()
Kettenregel:
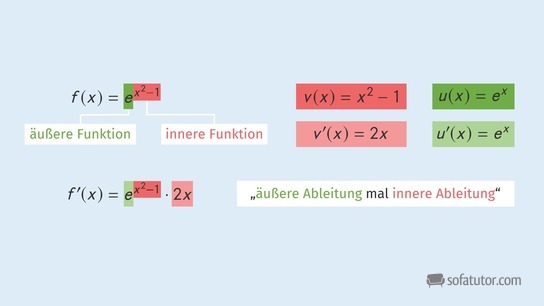
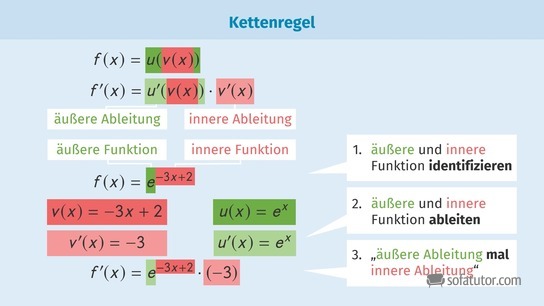
Die Kettenregel zum Ableiten verketteter Funktionen lautet:
![]()
Die Ableitung wird in zwei Schritten gebildet:
- Ableiten der äußeren Funktion mit der unveränderten inneren Funktion liefert den Term
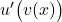 .
. - Dieser wird dann mit der Ableitung der inneren Funktion
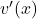 multipliziert. Dieser Schritt wird auch Nachdifferenzieren genannt.
multipliziert. Dieser Schritt wird auch Nachdifferenzieren genannt.
Beispiele:
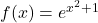
äußere Funktion: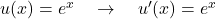
innere Funktion: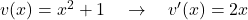
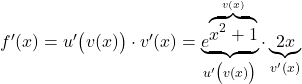
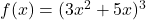
äußere Funktion: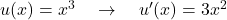
innere Funktion: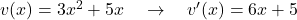
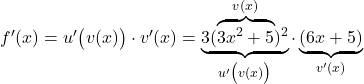
Herleitung der Kettenregel
Wir wollen nun die allgemeine Gültigkeit der Kettenregel durch eine Herleitung über den Differenzialquotienten zeigen.
Die Ableitung der Funktion ![]() an der Stelle
an der Stelle ![]() lautet mit dem Differenzialquotienten:
lautet mit dem Differenzialquotienten:
![]()
Erweitern des Bruchs mit ![]() liefert die Kettenregel:
liefert die Kettenregel:
![Rendered by QuickLaTeX.com \lim\limits_{x \to x_0} \frac{\Bigl[u\bigl(v(x)\bigr) - u\bigl(v(x_0)\bigr)\Bigr] \cdot \Bigl[v(x) - v(x_0)\Bigr]}{\Bigl[x - x_0\Bigr] \cdot \Bigl[v(x) - v(x_0)\Bigr]} = \lim\limits_{x \to x_0} \dfrac{u\bigl(v(x)\bigr) - u\bigl(v(x_0)\bigr)}{v(x) - v(x_0)} \cdot \dfrac{v(x) - v(x_0)}{x - x_0} = u^\prime\bigl(v(x)\bigr) \cdot v^\prime(x)](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-e684421708e72e7c899b3a867bd07b68_l3.png)
Anwendung der Kettenregel
Im Folgenden betrachten wir einige Beispiele für die Anwendung der Kettenregel bei verschiedenen Funktionstypen.
Kettenregel bei Wurzeln
Wir schreiben im ersten Schritt die Wurzel als Exponent und wenden dann die Kettenregel an.
![]()
![]()
![]()
![]()
Kettenregel bei verknüpften Funktionen mit Exponentialfunktionen
Wir betrachten die Funktion ![]() mit
mit ![]() . Für die Ableitung dieses Produkts aus einer ganzrationalen Funktion und einer e-Funktion werden die Produkt- und Kettenregel benötigt:
. Für die Ableitung dieses Produkts aus einer ganzrationalen Funktion und einer e-Funktion werden die Produkt- und Kettenregel benötigt:
Der Funktionsterm ist ein Produkt aus:
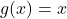 mit
mit 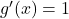
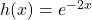 mit
mit 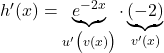 nach der Kettenregel
nach der Kettenregel
Wir erhalten:
![]()
Kettenregel beim Logarithmus
Auch bei Logarithmusfunktionen wird häufig die Kettenregel für die Ableitung benötigt. Wir betrachten die folgende Funktion:
![]()
Hier ist die äußere Funktion ![]() der natürliche Logarithmus mit der Ableitung
der natürliche Logarithmus mit der Ableitung ![]() . Die innere Funktion ist
. Die innere Funktion ist ![]() mit der Ableitung
mit der Ableitung ![]() .
.
Wir erhalten als Ableitung:
![]()
Kettenregel und Stammfunktion
Eine umgekehrte Anwendung der Kettenregel kann bei der Integration (umgangssprachlich auch aufleiten) von bestimmten Funktionen helfen.
Wir haben im letzten Beispiel gesehen, dass wir durch Anwendung der Kettenregel bei der ![]() -Funktion Brüche erhalten, bei denen im Zähler die Ableitung des Nenners steht. Daraus lässt sich die folgende Integrationsregel ableiten:
-Funktion Brüche erhalten, bei denen im Zähler die Ableitung des Nenners steht. Daraus lässt sich die folgende Integrationsregel ableiten:
![]()
Auch bei der natürlichen Exponentialfunktion erhalten wir durch allgemeine Betrachtung folgende Integrationsregel als Umkehrung der Kettenregel:
![]()
Ableitungsregeln im Überblick
Die folgende Tabelle fasst die wichtigsten Ableitungsregeln zusammen:
| Name | Funktion |
Ableitung |
|---|---|---|
| Faktorregel | ||
| Summenregel | ||
| Kettenregel | ||
| Produktregel | ||
| Quotientenregel |
Häufig gestellte Fragen zum Thema Kettenregel