Volumen und Oberfläche einer Pyramide berechnen

Die Pyramide ist ein geometrischer Körper mit Grund- und Seitenflächen. Lerne, wie man Oberfläche und Volumen berechnet, abhängig von der Grundfläche und den Höhen. Dies und vieles mehr findest du im folgenden Text!

Inhaltsverzeichnis zum Thema Pyramide berechnen

Pyramide berechnen im Überblick

  • Die Pyramide ist ein geometrischer Körper.

  • Die Oberfläche der Pyramide setzt sich aus Grund- und Mantelfläche zusammen. Der Flächeninhalt der Oberfläche kann mit der Formel O=G+M berechnet werden.

  • Das Volumen einer Pyramide wird mit der Formel V=\frac{1}{3} \cdot G \cdot h berechnet.

  • Die Berechnung von Grundfläche und Mantelfläche hängt von der Anzahl der Eckpunkte der Grundfläche ab.

Eigenschaften der Pyramide

Die Pyramide ist ein Körper. Sie besitzt eine Grundfläche und Seitenflächen. Alle Seitenflächen zusammen bilden die Mantelfläche. Während die Grundfläche ein beliebiges Vieleck sein kann, sind die Seitenflächen dreieckig.

Die Seitenflächen laufen nach oben zusammen und treffen sich in der Spitze der Pyramide.

Zur Berechnung der verschiedenen Flächen und des Volumens benötigst du

  • die Kantenlängen der Grundfläche,
  • die Höhe der Seitenflächen und
  • die Höhe der Pyramide.
Wichtige Größen einer Pyramide

Bei einer gleichseitigen Pyramide sind die Kantenlängen der Grundfläche alle gleich lang.

Oberfläche einer Pyramide berechnen

Die Oberfläche einer Pyramide besteht aus der Grundfläche und der Mantelfläche.
Entsprechend berechnest du die Oberfläche O einer Pyramide, indem du den Flächeninhalt der Grundfläche G mit den Flächeninhalten aller Seitenflächen, also der Mantelfläche M, addierst.

O=G+M

Grund- und Seitenflächen einer Pyramide

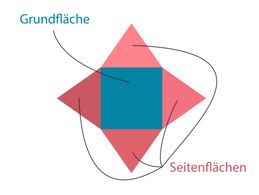
Je nach Form der Grundfläche unterscheidet sich die Berechnung der Oberfläche, da sich die Grundfläche und die Anzahl der Seitenflächen entsprechend ändern.

Die Grundfläche der Pyramide kann ein beliebiges Vieleck sein. Für die Berechnung ihres Flächeninhalts verwendest du die zugehörige Formel zur Flächenberechnung des Vielecks.
Eine häufig vorkommende Grundfläche ist das Quadrat. Man spricht dann von einer quadratischen Pyramide und berechnet den Flächeninhalt der Grundfläche mit G=a^{2}. Dabei ist a die Kantenlänge der Grundfläche. Etwas allgemeiner nennt man eine Pyramide regelmäßig, wenn die Grundfläche ein regelmäßiges Vieleck ist.

Die Mantelfläche ergibt sich aus der Summe der Seitenflächen. Die Anzahl der Seitenflächen hängt von der Grundfläche ab.
Hat die Pyramide ein Dreieck als Grundfläche, besitzt diese drei Seitenflächen. Bei einer viereckigen Grundfläche sind es vier und so weiter. Die Pyramide besitzt also immer so viele Seiten, wie ihre Grundfläche Ecken bzw. Kanten hat.
Die Seitenflächen sind stets dreieckig. Du berechnest die Mantelfläche einer regelmäßigen Pyramide, indem du den Flächeninhalt der dreieckigen Seitenflächen mit der Anzahl der Seitenflächen multiplizierst.

Bei der quadratischen Pyramide berechnest du die Mantelfläche also mit der Formel:
M=\left(\dfrac{1}{2} \cdot a \cdot h_{\triangle} \right) \cdot 4

Beispiel Oberflächenberechnung – Pyramide mit dreieckiger Grundfläche

Dir ist eine regelmäßige dreiseitige Pyramide gegeben. Die Grundfläche ist also ein gleichseitiges Dreieck der Kantenlänge a=10~\text{cm} und mit der Höhe h=8,\!66~\text{cm}. Die Höhe der Seitenflächen ist gegeben durch h_{\triangle}=9~\text{cm}.

Dreiseitige Pyramide

Zur Berechnung des Flächeninhalts der Oberfläche berechnest du zunächst den Flächeninhalt der Grundfläche.

G=\dfrac{1}{2} \cdot 10~\text{cm} \cdot 8,\!66~\text{cm}=43,\!3~\text{cm}^{2}

Anschließend berechnest du den Flächeninhalt aller Seitenflächen.

M=3 \cdot 10~\text{cm} \cdot 9~\text{cm}= 270~\text{cm}^{2}

Addiere nun die Flächeninhalte von Grund- und Mantelfläche und du erhältst den Flächeninhalt der Oberfläche der dreiseitigen Pyramide.

O=G+M=43,\!3~\text{cm}^{2}+270~\text{cm}^{2}=313,\!3~\text{cm}^{2}

Volumen einer Pyramide berechnen – Formel

Zur Volumenberechnung einer Pyramide benötigst du die Höhe h der Pyramide und die Grundfläche G. Diese multiplizierst du miteinander und mit einem Drittel und erhältst so das Volumen der Pyramide.

V=\dfrac{1}{3} \cdot G \cdot h

Anstelle des Volumens spricht man auch vom Rauminhalt der Pyramide.

Volumen Pyramide – Herleitung

Um zu zeigen, dass das Volumen einer Pyramide mit der Formel V=\frac{1}{3} \cdot G \cdot h berechnet werden kann, greifen wir auf das Volumen des Würfels mit Kantenlänge a zurück.

Das Volumen des Würfels ist a^{3}.
Betrachte nun die quadratische Pyramide mit Kantenlänge a und Höhe h=\dfrac{1}{2} \cdot a.

In den Würfel passen sechs dieser Pyramiden, wie du im folgenden Bild erkennen kannst.

Herleitung des Volumens einer Pyramide

Es gilt also

V_{\text{Würfel}}=6 \cdot V_{\text{Pyramide}}

Wir setzen die Formel für das Würfelvolumen V_{\text{Würfel}}=a^3 ein und lösen die Formel nach dem Pyramidenvolumen auf:

V_{\text{Pyramide}}= \dfrac{1}{6} V_{\text{Würfel}}= \dfrac{1}{6} a^3 = \dfrac{1}{3} \cdot \dfrac{a}{2} \cdot a^2 = \dfrac{1}{3} \cdot G \cdot h

Dadurch ist die Formel V=\dfrac{1}{3} \cdot G \cdot h für diese Pyramide bewiesen. Die Formel gilt für alle Pyramiden, unabhängig von der Form und von der Grundfläche.

Formelsammlung Pyramide

Allgemein berechnest du die Oberfläche und das Volumen einer Pyramide durch die in der Tabelle angegebenen Formeln.

Berechnung von Formel
Oberfläche O O=G+M
Volumen V V=\dfrac{1}{3} \cdot G \cdot h

Für die konkrete Berechnung der verschiedenen Arten von Pyramiden kannst du dich an den folgenden Tabellen orientieren.

Bei einer dreiseitigen regulären Pyramide benötigst du zur Berechnung von Oberfläche und Volumen die Kantenlänge a des gleichseitigen Dreiecks, das die Grundfläche bildet, sowie dessen Höhe h_a, außerdem die Höhe h_\triangle der Seitenflächen und schließlich die räumliche Höhe h der Pyramide.

Dreiseitige Pyramide
Oberflächeninhalt O=\left( \dfrac{1}{2} \cdot a \cdot h_a \right)+3\cdot \left( \dfrac{1}{2} \cdot a \cdot h_{\triangle} \right)
Volumen V=\dfrac{1}{3}\left( \dfrac{1}{2} \cdot a \cdot h_{\triangle} \right) \cdot h

Ist die Höhe h_a der Grundfläche nicht gegeben, kannst du sie aus der Grundseite a berechnen. Ebenso kannst du die Höhe h_\triangle der Seitenfläche und die Höhe h der Pyramide aus der Grundseite a und einem Schenkel der Seitenflächen berechnen.

Zur Berechnung von Oberfläche und Volumen einer regulären quadratischen Pyramide benötigst du nur die Grundseite a, die Höhe h_\triangle der Seitenflächen und die räumliche Höhe h der Pyramide.

Quadratische Pyramide
Oberflächeninhalt O=\left(a^{2}\right)+4\cdot \left( \dfrac{1}{2} \cdot a \cdot h_{\triangle} \right)
Volumen V=\dfrac{1}{3} \cdot \left(a^{2}\right) \cdot h

Ist nur eine der Größen h_\triangle und h gegeben oder stattdessen ein Schenkel der Seitenflächen, kannst du h_\triangle und h daraus berechnen.

Häufig gestellte Fragen zum Thema Pyramide berechnen

Wie viele Ecken eine Pyramide hat, hängt davon ab, wie viele Ecken die Grundfläche hat. Zusätzlich zur Spitze besitzt die Pyramide noch die Ecken ihrer Grundfläche. So hat eine dreiseitige Pyramide vier Ecken, nämlich die Spitze und die drei Ecken der Grundfläche.

Die Anzahl der Kanten einer Pyramide hängt von der Grundfläche ab. Zusätzlich zu den Kanten der Grundfläche führt von jeder Ecke der Grundfläche eine Kante zur Spitze der Pyramide.

Eine Pyramide besitzt eine Grundfläche und mehrere Seitenflächen. Die Grundfläche bildet zusammen mit allen Seitenflächen die Oberfläche der Pyramide. Die Anzahl der Seitenflächen ist das Gleiche wie die Anzahl der Eckpunkte oder der Kanten der Grundfläche. Die Pyramide hat also eine Fläche mehr, als die Grundfläche Eckpunkte hat.

Die Mantelfläche setzt sich aus allen Seitenflächen der Pyramide zusammen. Der Flächeninhalt der Mantelfläche ist die Summe der Flächeninhalte aller Seitenflächen.

Das Volumen einer Pyramide kannst du mit der Formel V=\frac{1}{3} \cdot G \cdot h berechnen. Dabei ist G die Grundfläche und h die räumliche Höhe der Pyramide. Die genaue Formel hängt von der Form der Grundfläche ab.

Eine Pyramide setzt sich aus einer Grundfläche und mehreren Seitenflächen zusammen. Die Grundfläche ist ein beliebiges Vieleck und die Seitenflächen sind dreieckig. Die Seitenflächen laufen an der Spitze der Pyramide zusammen.

Der Mantel wird auch Mantelfläche genannt. Er setzt sich zusammen aus allen Seitenflächen der Pyramide.

Eine Pyramide berechnet man mit den Formeln für den Oberflächeninhalt und für das Volumen. Diese lauten:

Hierbei ist G die Grundfläche der Pyramide, M die Mantelfläche und h die räumliche Höhe der Pyramide.

Die Grundfläche einer Pyramide kann ein beliebiges Vieleck sein. Den Flächeninhalt der Grundfläche berechnest du mit der Formel zur Flächenberechnung des jeweiligen Vielecks.

Die Grundfläche einer Pyramide ist das Vieleck, das den Boden bildet, auf dem die Pyramide steht.

Den Flächeninhalt der Seitenfläche einer quadratischen Pyramide berechnest du mit der Formel für den Flächeninhalt eines Dreiecks: \frac{1}{2} \cdot a \cdot h_\triangle. Hierbei ist h_\triangle die Höhe der Seitenfläche.

Die Seiten einer Pyramide sind dreieckig. Entsprechend berechnest du den Flächeninhalt der Seitenflächen mit der Formel \frac{1}{2} \cdot a \cdot h_\triangle.  Hierbei ist a die Grundseite einer Seitenfläche und h_\triangle die zugehörige Höhe dieser Seitenfläche.

Für die Berechnung des Flächeninhalts der Grundfläche einer dreiseitigen Pyramide greifst du auf die Formel zur Berechnung des Flächeninhalts eines Dreiecks zurück. Diese lautet: \frac{1}{2} \cdot a \cdot h_a. Hierbei ist h_a die zu der Seite a gehörige Höhe der Grundfläche. Ist die Grundfläche ein gleichseitiges Dreieck mit Kantenlänge a, ist h_a=\frac{\sqrt{3}}{2}\cdot a \approx 0,\!866 \cdot a.

Die Grundfläche einer rechteckigen Pyramide berechnest du, indem du die beiden Seitenlängen a und b der Grundfläche miteinander multiplizierst. In diesem Fall lautet die Formel für die Grundfläche also G=a \cdot b.

Leave A Comment

Alle Artikel aus dem Fach Mathematik