Flächeninhalt berechnen – Mathe

Lerne, was der Flächeninhalt einer Figur ist und wie er berechnet wird. Entdecke Formeln für Quadrat, Rechteck, Dreieck und Kreis sowie spezielle Fälle. Interessiert? Dies und vieles mehr findest du im folgenden Text!

Inhaltsverzeichnis zum Thema Flächeninhalt

Flächeninhalt im Überblick
Flächeninhalt – Definition
Flächeninhalt einer Figur berechnen
Flächeninhalt berechnen – Quadrat
Flächeninhalt berechnen – Rechteck
Flächeninhalt berechnen – Dreieck
Flächeninhalt berechnen – Kreis
Flächeninhalte weiterer Formen berechnen
Flächeninhalt zusammengesetzter Flächen bestimmen
Häufig gestellte Fragen zum Thema Flächeninhalt

Das Quiz zum Thema: Flächeninhalt

Wie wird der Flächeninhalt eines Quadrats berechnet?

Frage 1 von 5

Wie wird der Flächeninhalt eines Rechtecks berechnet?

Frage 2 von 5

Wie wird der Flächeninhalt eines Dreiecks berechnet?

Frage 3 von 5

Wie wird der Flächeninhalt eines Kreises berechnet?

Frage 4 von 5

Wie kann die Fläche von zusammengesetzten Flächen bestimmt werden?

Frage 5 von 5

Flächeninhalt im Überblick

Als Flächeninhalt wird die von einer Figur eingeschlossene Fläche bezeichnet.
In Mathe werden Flächeninhalte meist mit dem Buchstaben $A$ bezeichnet.
Die Berechnung des Flächeninhalts hängt von der Form der Figur ab.

Quelle sofatutor.com

Flächeninhalt – Definition

Die Fläche, die durch den Rand einer geometrischen Figur eingeschlossen wird, ist der Flächeninhalt.
Geometrische Figuren sind zum Beispiel Dreiecke, Kreise und Rechtecke. Aber auch komplizierte zusammengesetzte Formen besitzen einen Flächeninhalt, den wir berechnen können.
Beachte: Flächen sind immer zweidimensional. Das heißt, sie besitzen keine Höhe. Flächen haben nur eine Länge und eine Breite.

Das Zeichen für den Flächeninhalt ist in der Mathematik ein $A$ . Die Einheit des Flächeninhalts ist eine Längeneinheit ins Quadrat gesetzt, so zum Beispiel Quadratmeter oder Quadratzentimeter. Das schreiben wir als $\text{m}^2$ und $\text{cm}^2$ . Bei diesen Einheiten spricht man auch vom Flächenmaß.

Flächeninhalt einer Figur berechnen

Die Formeln zur Berechnung des Flächeninhalts hängen von der Form der Figuren ab. Einige der wichtigsten Formen schauen wir uns im Folgenden genauer an.

Flächeninhalt berechnen – Quadrat

Den Flächeninhalt $A$ eines Quadrats berechnen wir mit der Formel:

$A = a \cdot a = a^2$

Dabei ist $a$ die Seitenlänge des Quadrats. Alle Seiten des Quadrats sind immer gleich lang.

Beispiel:
Betrachten wir ein Quadrat mit der Seitenlänge $a = 5~\text{cm}$ . Der Flächeninhalt des Quadrats ist dann:

$A = 5~\text{cm} \cdot 5~\text{cm} = 25~\text{cm}^2$

Flächeninhalt berechnen – Rechteck

Um den Flächeninhalt $A$ von einem Rechteck zu berechnen, nutzen wir die Formel:

$A = a \cdot b$

Dabei sind $a$ und $b$ die Seitenlängen des Rechtecks. Die gegenüberliegenden Seiten im Rechteck sind immer parallel und gleich lang.

Beispiel:
Betrachten wir ein Rechteck mit den Seitenlängen $a = 3~\text{cm}$ und $b = 5~\text{cm}$ . Der Flächeninhalt des Rechtecks ist dann:

$A = 3~\text{cm} \cdot 5~\text{cm} = 15~\text{cm}^2$

Flächeninhalt berechnen – Dreieck

Den Flächeninhalt $A$ eines Dreiecks berechnen wir mit der Formel:

$A = \dfrac{1}{2} \cdot g \cdot h_g$

Dabei ist $g$ eine der drei Seiten des Dreiecks. Die dazugehörige Höhe ist $h_g$ .

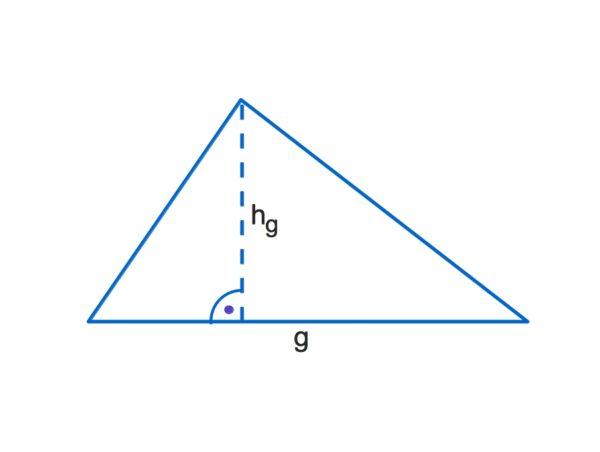
Beispiel:
Betrachten wir ein Dreieck mit der Seitenlänge $c = 7~\text{cm}$ und der dazugehörigen Höhe $h_c = 4~\text{cm}$ . Der Flächeninhalt des Dreiecks ist dann:

$A = \dfrac{1}{2} \cdot 7~\text{cm} \cdot 4~\text{cm} = 14~\text{cm}^2$

rechtwinkliges Dreieck
Um den Flächeninhalt eines rechtwinkligen Dreiecks zu berechnen, können wir auch eine andere Formel verwenden.

$A = \dfrac{1}{2} \cdot a \cdot b$

Dabei sind $a$ und $b$ die am rechten Winkel anliegenden Seiten (Katheten).

Flächeninhalt berechnen – Kreis

Den Flächeninhalt $A$ eines Kreises berechnen wir mit der Formel:

$A = \pi \cdot r^2$

Dabei ist $r$ der Radius des Kreises. Die Kreiszahl $\pi$ (Pi) ist fest definiert und ungefähr $3,\!14$ . Ist statt des Radius nur der Durchmesser $d$ gegeben, dann lautet die Formel:

$A = \pi \cdot \left(\dfrac{d}{2}\right)^2$

Beispiel:
Betrachten wir einen Kreis mit einem Radius von $r = 6~\text{cm}$ . Der Flächeninhalt des Kreises ist dann:

$A = \pi \cdot (6~\text{cm})^2 \approx 113,\!1\,\text{cm}^2$

Flächeninhalte weiterer Formen berechnen

Die folgende Tabelle zeigt die Berechnung des Flächeninhalts weiterer geometrischer Formen.

Geometrische Form	Flächeninhalt Formel	Bedeutung der Größen
Parallelogramm	$A = a \cdot h_a$	$a$ : eine der Seitenlängen $a_h$ : Abstand zur gegenüberliegenden Seite
Trapez	$A = \dfrac{1}{2} \cdot (a + c) cdot h$	$a$ und $c$ : gegenüberliegende, parallele Seiten $h$ : Abstand zwischen $a$ und $c$
Raute	$A = a \cdot h$	$a$ : Seitenlänge (alle Seiten sind gleich lang) $h$ : Abstand zwischen zwei parallelen Seiten
regelmäßiges Sechseck	$A = \dfrac{3 \cdot \sqrt{3} \cdot a^2}{2}$	$a$ : Seitenlänge (alle sechs Seiten sind gleich lang)
Drachenviereck	$A = \dfrac{1}{2} \cdot e \cdot f$	$e$ und $f$ : Diagonalen (stehen senkrecht aufeinander)

In den meisten Formeln spielt die Seitenlänge eine Rolle. Bei diesen Figuren kann dann umgekehrt auch die Seitenlänge aus dem Flächeninhalt berechnet werden. Dafür können die Formeln so umgestellt werden, dass die Seitenlänge allein auf einer Seite der Gleichung steht.

Flächeninhalt zusammengesetzter Flächen bestimmen

Zusammengesetzte Flächen setzen sich aus verschiedenen geometrischen Formen zusammen. Um den Flächeninhalt zusammengesetzter Flächen zu berechnen, gehen wir so vor:

Schritt 1: zusammengesetzte Fläche in bekannte Formen zerlegen
Schritt 2: Flächeninhalt der einzelnen Formen berechnen
Schritt 3: alle berechneten Teilflächen addieren

Beispiel:
Betrachten wir die folgende Figur.

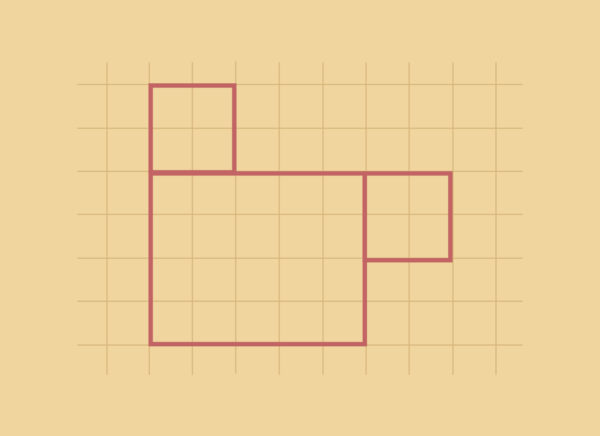
Sie besteht aus drei Teilen. Wir berechnen also zuerst die einzelnen Flächeninhalte. Ein Kästchen hat die Breite $1~\text{cm}$ . Die einzelnen Flächeninhalte sind:

Quadrat oben: $A_1 = 2~\text{cm} \cdot 2~\text{cm} = 4~\text{cm}^2$
Quadrat rechts: $A_2 = 2~\text{cm} \cdot 2~\text{cm} = 4~\text{cm}^2$
Rechteck: $A_3 = 5~\text{cm} \cdot 4~\text{cm} = 20~\text{cm}^2$

Jetzt können wir alle drei Flächeninhalte addieren und so den Gesamtflächeninhalt ausrechnen:

$A_{gesamt} = 4~\text{cm}^2 + 4~\text{cm}^2 + 20~\text{cm}^2 = 28~\text{cm}^2$

Häufig gestellte Fragen zum Thema Flächeninhalt

Was ist ein Flächeninhalt?

Der Flächeninhalt ist die Größe der Fläche, die von einer Figur eingeschlossen wird.

Wie berechnet man einen Flächeninhalt?

Die Berechnung des Flächeninhalts hängt von der Form der Figur ab.

Wie berechnet man den Flächeninhalt eines Rechtecks?

Den Flächeninhalt eines Rechtecks berechnen wir mit der Formel $A = a \cdot b$ .

Wie lautet die Formel für den Flächeninhalt eines Parallelogramms?

Den Flächeninhalt eines Parallelogramms berechnen wir mit der Formel $A = a \cdot h_a$ .

Wie berechnet man den Flächeninhalt eines Kreises mit dem Durchmesser?

Ist der Durchmesser $d$ gegeben, dann können wir den Flächeninhalt eines Kreises mit der Formel $A = \pi \cdot (\frac{d}{2})^2$ berechnen.

Wie kann ich die Fläche von zusammengesetzten Flächen bestimmen?

Zuerst zerlegen wir die zusammengesetzten Flächen in uns bekannte Flächen. Dann können wir die Flächeninhalte der Teilflächen einzeln berechnen. Zuletzt addieren wir alle berechneten Flächeninhalte der Teilflächen und erhalten den gesamten Flächeninhalt.

Super! Das Thema: kannst du schon! Teile deine Learnings und Fragen mit der Community! Antworten abbrechen

Alle Artikel aus dem Fach Mathematik

Flächeninhalt berechnen – Mathe

Inhaltsverzeichnis zum Thema Flächeninhalt

Das Quiz zum Thema: Flächeninhalt

Flächeninhalt im Überblick

Wie willst du heute lernen?

Super! Das Thema: kannst du schon! Teile deine Learnings und Fragen mit der Community! Antworten abbrechen