Der Sinus – Definition, Eigenschaften und Anwendungen
Der Sinus im rechtwinkligen Dreieck erklärt! Verstehe die Definition, Zusammenhänge mit Cosinus und Tangens, Einheitskreis-Anwendung und mehr. Dies und vieles mehr findest du im folgenden Text.
Inhaltsverzeichnis zum Thema Sinus
Der Sinus im Überblick
Der Sinus im rechtwinkligen Dreieck – Definition und Eigenschaften
In diesem Text wird dir der Sinus einfach erklärt. Wir schauen uns die Eigenschaften des Sinus an und erklären, wie der Sinus mit Cosinus und Tangens zusammenhängt und wie man den Sinus am Einheitskreis verstehen kann.
Sinus, Cosinus und Tangens – Definition
In einem rechtwinkligen Dreieck heißen die beiden kürzeren Seiten, die an dem rechten Winkel anliegen, die Katheten des Dreiecks. Die längste Seite des rechtwinkligen Dreiecks liegt dem rechten Winkel gegenüber und heißt Hypotenuse. Die Winkel im rechtwinkligen Dreieck bezeichnet man oft mit ![]() ,
, ![]() und
und ![]() und verwendet dabei
und verwendet dabei ![]() für den rechten Winkel.
für den rechten Winkel.
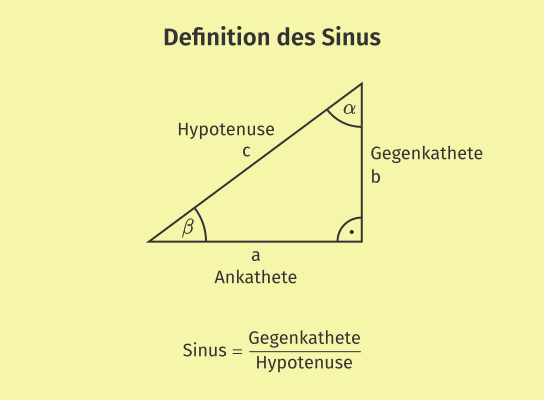
Ist ![]() einer der beiden spitzen Winkel eines rechtwinkligen Dreiecks, nennt man die dem Winkel gegenüberliegende Kathete die Gegenkathete von
einer der beiden spitzen Winkel eines rechtwinkligen Dreiecks, nennt man die dem Winkel gegenüberliegende Kathete die Gegenkathete von ![]() . Die Kathete, die an dem Winkel anliegt, heißt Ankathete von
. Die Kathete, die an dem Winkel anliegt, heißt Ankathete von ![]() . Der Sinus des Winkel ist das Längenverhältnis der Gegenkathete von
. Der Sinus des Winkel ist das Längenverhältnis der Gegenkathete von ![]() zur Hypotenuse:
zur Hypotenuse:
![]()
Der Sinus eines Winkels ist nur in einem rechtwinkligen Dreieck definiert, denn nur dort gibt es Katheten und eine Hypotenuse. Der Sinus ist nur für die beiden spitzen Winkel definiert.
Den Sinus bezeichnet man auch als trigonometrische Funktion. Andere trigonometrische Funktionen sind Cosinus und Tangens. Sie lassen sich unter den gleichen Voraussetzungen wie der Sinus erklären: Der Cosinus eines spitzen Winkels im rechtwinkligen Dreieck ist das Längenverhältnis der Ankathete des Winkels zur Hypotenuse:
![]()
Der Tangens eines solchen Winkels ist das Längenverhältnis der Gegenkathete zur Ankathete:
![]()
In der folgenden Tabelle sind die Definitionen auf einen Blick zusammengefasst:
| Trigonometrische Größe | Definition | Formel |
|---|---|---|
| Sinus von |
||
| Cosinus von |
||
| Tangens von |
Sinus, Cosinus und Tangens – Zusammenhang und Eigenschaften
- In einem rechtwinkligen Dreieck mit dem rechten Winkel
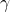 und den beiden spitzen Winkeln
und den beiden spitzen Winkeln 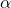 und
und 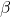 ist die Gegenkathete von
ist die Gegenkathete von 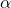 das Gleiche wie die Ankathete von
das Gleiche wie die Ankathete von 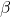 – und umgekehrt. Daher ist der Sinus des Winkels
– und umgekehrt. Daher ist der Sinus des Winkels 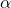 das Gleiche wie der Cosinus des Winkels
das Gleiche wie der Cosinus des Winkels 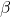 – und umgekehrt:
– und umgekehrt:

Mit anderen Worten: Ergänzen sich zwei Winkel ![]() und
und ![]() zu
zu ![]() , ist:
, ist:
 und
und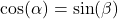 .
.
Im Folgenden bezeichnen wir solche Winkel als Ergänzungswinkel zu ![]() .
.
- Der Tangens eines Winkels im rechtwinkligen Dreieck ist definiert als das Längenverhältnis der Gegenkathete zur Ankathete. Erweitert man den Bruch mit dem Kehrwert der Hypotenuse, erhält man das Verhältnis von Sinus und Cosinus:

- Im rechtwinkligen Dreieck hängen die Seitenlängen über den Satz des Pythagoras miteinander zusammen. In Worten und in Formeln besagt der Satz des Pythagoras:

Dividierst du in dieser Gleichung beide Seiten durch ![]() , erhältst du:
, erhältst du:

In der folgenden Tabelle sind die wichtigsten Zusammenhänge der trigonometrischen Größen im rechtwinkligen Dreieck auf einen Blick zusammengefasst:
| Trigonometrische Größe | Formel |
|---|---|
| Gegenwinkel | |
| Sinus des Gegenwinkels | |
| Cosinus des Gegenwinkels | |
| Satz des Pythagoras | |
| Tangens |
Wertebereiche des Sinus, Cosinus und Tangens im rechtwinkligen Dreieck
In einem rechtwinkligen Dreieck haben die beiden spitzen Winkel immer Winkelgrößen zwischen ![]() und
und ![]() . Sie sind also größer als
. Sie sind also größer als ![]() und kleiner als
und kleiner als ![]() . Da die beiden Katheten eines rechtwinkligen Dreiecks immer kürzer sind als die Hypotenuse, ist der Wert des Sinus und des Cosinus eines Winkels
. Da die beiden Katheten eines rechtwinkligen Dreiecks immer kürzer sind als die Hypotenuse, ist der Wert des Sinus und des Cosinus eines Winkels ![]() immer kleiner als
immer kleiner als ![]() . Da die Längen alle positiv sind, ist der Wert stets größer als
. Da die Längen alle positiv sind, ist der Wert stets größer als ![]() . Für Winkelgrößen zwischen
. Für Winkelgrößen zwischen ![]() und
und ![]() liegen die Werte des Sinus und Cosinus also zwischen
liegen die Werte des Sinus und Cosinus also zwischen ![]() und
und ![]() .
.
Auch das Längenverhältnis von Gegenkathete und Ankathete ist stets positiv. Es kann aber beliebig groß werden, da es auch sehr schmale und spitze rechtwinklige Dreiecke gibt. Für Winkelgrößen zwischen ![]() und
und ![]() liegen die Werte des Tangens daher zwischen
liegen die Werte des Tangens daher zwischen ![]() und
und ![]() .
.
Spezielle Werte des Sinus und Cosinus
Für einige spezielle Dreiecke kannst du die Werte des Sinus und Cosinus im Kopf oder mit dem Satz des Pythagoras berechnen:
Gleichschenklige Dreiecke
Sind die beiden Katheten des rechtwinkligen Dreiecks gleich lang (![]() ), sind auch die beiden spitzen Winkel gleich groß (
), sind auch die beiden spitzen Winkel gleich groß (![]() ). Da die Innenwinkelsumme im Dreieck stets
). Da die Innenwinkelsumme im Dreieck stets ![]() beträgt, haben die beiden spitzen Winkel die Winkelgröße
beträgt, haben die beiden spitzen Winkel die Winkelgröße ![]() . Den Sinus und den Cosinus von
. Den Sinus und den Cosinus von ![]() kannst du direkt ausrechnen: Haben die Katheten die Länge
kannst du direkt ausrechnen: Haben die Katheten die Länge ![]() , hat die Hypotenuse nach dem Satz des Pythagoras die Länge
, hat die Hypotenuse nach dem Satz des Pythagoras die Länge ![]() . Für den Sinus und Cosinus von
. Für den Sinus und Cosinus von ![]() erhältst du dann:
erhältst du dann:
![]()
Für den Cosinus des Winkels erhältst du genau den gleichen Wert, denn ![]() . Den exakten Wert
. Den exakten Wert ![]() haben wir ohne Taschenrechner berechnet. Mit dem Taschenrechner kannst du aus dem exakten Wert einen Näherungswert als Dezimalzahl bestimmen und erhältst:
haben wir ohne Taschenrechner berechnet. Mit dem Taschenrechner kannst du aus dem exakten Wert einen Näherungswert als Dezimalzahl bestimmen und erhältst: ![]() .
.
Gleichseitige Dreiecke
Ein gleichseitiges Dreieck hat drei gleich lange Seiten und drei gleich große Winkel der Winkelgröße ![]() . Ein gleichseitiges Dreieck ist also nicht rechtwinklig. In einem gleichseitigen Dreieck sind die Höhen, Winkelhalbierenden, Seitenhalbierenden und Mittelsenkrechten identisch. Halbierst du ein gleichseitiges Dreieck durch eine solche Strecke, erhältst du zwei kongruente rechtwinklige Dreiecke mit den spitzen Winkeln
. Ein gleichseitiges Dreieck ist also nicht rechtwinklig. In einem gleichseitigen Dreieck sind die Höhen, Winkelhalbierenden, Seitenhalbierenden und Mittelsenkrechten identisch. Halbierst du ein gleichseitiges Dreieck durch eine solche Strecke, erhältst du zwei kongruente rechtwinklige Dreiecke mit den spitzen Winkeln ![]() und
und ![]() . Der halbierte Winkel
. Der halbierte Winkel ![]() liegt gegenüber der halbierten Seite des gleichseitigen Dreiecks. Der Winkel
liegt gegenüber der halbierten Seite des gleichseitigen Dreiecks. Der Winkel ![]() liegt gegenüber der Höhe des gleichseitigen Dreiecks.
liegt gegenüber der Höhe des gleichseitigen Dreiecks.
Die Hypotenuse des rechtwinkligen Dreiecks ist eine Seite ![]() des gleichseitigen Dreiecks. Die dem halbierten Winkel
des gleichseitigen Dreiecks. Die dem halbierten Winkel ![]() gegenüberliegende Kathete
gegenüberliegende Kathete ![]() hat dann die Seitenlänge
hat dann die Seitenlänge ![]() . Die dem Winkel
. Die dem Winkel ![]() gegenüberliegende Seite
gegenüberliegende Seite ![]() ist die Höhe des gleichseitigen Dreiecks.
ist die Höhe des gleichseitigen Dreiecks.
Für den Sinus des Winkels ![]() berechnen wir:
berechnen wir:
![]()
Dieser Wert ist der gleiche wie der Cosinus des Gegenwinkels: ![]() .
.
Um den Sinus des Winkels ![]() zu berechnen, benötigen wir die Länge der Gegenkathete
zu berechnen, benötigen wir die Länge der Gegenkathete ![]() von
von ![]() . Dies ist das Gleiche wie die Höhe des gleichseitigen Dreiecks.
. Dies ist das Gleiche wie die Höhe des gleichseitigen Dreiecks.
Diese Länge kannst du mit dem Satz des Pythagoras berechnen:
![]()
Nun können wir auch den Sinus des Winkels ![]() einfach berechnen:
einfach berechnen:
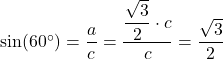
Diesen exakten Wert des Sinus haben wir ohne Taschenrechner berechnet. Mit dem Taschenrechner kannst du daraus einen Näherungswert als Dezimalzahl bestimmen und erhältst: ![]() .
.
Ausgeartete Dreiecke
Stell dir vor, du machst ein rechtwinkliges Dreieck immer spitzer, sodass die Länge der Kathete ![]() immer kleiner wird, aber die Länge der Hypotenuse gleich bleibt. Dann wird auch der Winkel
immer kleiner wird, aber die Länge der Hypotenuse gleich bleibt. Dann wird auch der Winkel ![]() immer kleiner. Du kannst dir vorstellen, wie die Winkelgröße von
immer kleiner. Du kannst dir vorstellen, wie die Winkelgröße von ![]() zu
zu ![]() wird und gleichzeitig die Länge der Kathete
wird und gleichzeitig die Länge der Kathete ![]() auch
auch ![]() wird. Weil sich die Länge der Hypotenuse gar nicht geändert hat, kannst du immer noch den Sinus berechnen und erhältst:
wird. Weil sich die Länge der Hypotenuse gar nicht geändert hat, kannst du immer noch den Sinus berechnen und erhältst:
![]()
Wenn in deinem Dreieck der Winkel ![]() zu
zu ![]() wird, muss der Winkel
wird, muss der Winkel ![]() zu
zu ![]() werden, denn die Winkelsumme im Dreieck beträgt stets
werden, denn die Winkelsumme im Dreieck beträgt stets ![]() . Du hast also gerade eben auch den Cosinus von
. Du hast also gerade eben auch den Cosinus von ![]() berechnet:
berechnet:
![]()
Nun kannst du dir auch vorstellen, dass du das Dreieck immer flacher werden lässt, bis der Winkel ![]() zu
zu ![]() wird. In diesem Fall wird die Seite
wird. In diesem Fall wird die Seite ![]() zu
zu ![]() . Die Winkelsumme im Dreieck bleibt
. Die Winkelsumme im Dreieck bleibt ![]() , daher muss der Winkel
, daher muss der Winkel ![]() zu
zu ![]() werden. Und auch der Satz des Pythagoras bleibt erhalten. Wenn du in die Formel
werden. Und auch der Satz des Pythagoras bleibt erhalten. Wenn du in die Formel ![]() die Länge
die Länge ![]() einsetzt, ergibt sich:
einsetzt, ergibt sich: ![]() , also auch
, also auch ![]() . Jetzt kannst du wieder den Sinus berechnen:
. Jetzt kannst du wieder den Sinus berechnen:
![]()
Und wieder gilt ganz analog wie zuvor:
![]() , also
, also ![]()
Übersicht – spezielle Werte des Sinus
In der folgenden Tabelle fassen wir die wichtigsten Funktionswerte des Sinus zusammen.
Der Sinus im Einheitskreis
Der Einheitskreis ist ein Kreis im Koordinatensystem mit dem Radius ![]() und dem Mittelpunkt
und dem Mittelpunkt ![]() ). Jeder Punkt auf dem Einheitskreis ist durch seine Koordinaten
). Jeder Punkt auf dem Einheitskreis ist durch seine Koordinaten ![]() eindeutig festgelegt.
eindeutig festgelegt.

Der Radius ist die Strecke vom Mittelpunkt des Kreises zu dem Punkt ![]() . Zeichnest du von dem Punkt
. Zeichnest du von dem Punkt ![]() das Lot auf die
das Lot auf die ![]() -Achse, erhältst du ein rechtwinkliges Dreieck. Die Hypotenuse dieses Dreiecks ist der Radius. Die Hypotenuse hat also die Länge
-Achse, erhältst du ein rechtwinkliges Dreieck. Die Hypotenuse dieses Dreiecks ist der Radius. Die Hypotenuse hat also die Länge ![]() . Die Längen der Katheten sind die Werte der Koordinaten des Punkts. Die horizontale Kathete hat die Länge
. Die Längen der Katheten sind die Werte der Koordinaten des Punkts. Die horizontale Kathete hat die Länge ![]() , die vertikale Kathete die Länge
, die vertikale Kathete die Länge ![]() .
.
Formeln des Sinus, Cosinus und Tangens im Einheitskreis
Wir betrachten zunächst nur den ersten Quadranten des Einheitskreises, also den Bereich, in dem beide Koordinaten Werte ![]() annehmen. Zu einem Punkt
annehmen. Zu einem Punkt ![]() auf dem Einheitskreis zeichnen wir den Radius ein, also die Verbindungsstrecke zwischen dem Koordinatenursprung
auf dem Einheitskreis zeichnen wir den Radius ein, also die Verbindungsstrecke zwischen dem Koordinatenursprung ![]() und dem Punkt
und dem Punkt ![]() . Den Winkel zwischen der
. Den Winkel zwischen der ![]() -Achse und diesem Radius nennen wir
-Achse und diesem Radius nennen wir ![]() .
.
Von dem Punkt ![]() fällen wir das Lot auf die
fällen wir das Lot auf die ![]() -Achse und erhalten den Punkt
-Achse und erhalten den Punkt ![]() . Die Punkte
. Die Punkte ![]() ,
, ![]() und
und ![]() bilden ein rechtwinkliges Dreieck. Die Hypotenuse ist die Strecke
bilden ein rechtwinkliges Dreieck. Die Hypotenuse ist die Strecke ![]() , also der Radius zum Punkt
, also der Radius zum Punkt ![]() . Sie hat die Länge
. Sie hat die Länge ![]() , da der Punkt auf dem Einheitskreis liegt. Die Gegenkathete des Winkels
, da der Punkt auf dem Einheitskreis liegt. Die Gegenkathete des Winkels ![]() verläuft vertikal und hat die Länge
verläuft vertikal und hat die Länge ![]() . Die Ankathete verläuft horizontal und hat die Länge
. Die Ankathete verläuft horizontal und hat die Länge ![]() .
.
Die Koordinaten des Punkts ![]() auf dem Einheitskreis sind also die Längen der beiden Katheten in dem rechtwinkligen Dreieck
auf dem Einheitskreis sind also die Längen der beiden Katheten in dem rechtwinkligen Dreieck ![]() . Wir können den Sinus, Cosinus und Tangens des Winkels
. Wir können den Sinus, Cosinus und Tangens des Winkels ![]() durch die Koordinaten
durch die Koordinaten ![]() des Punkts auf dem Einheitskreis ausdrücken:
des Punkts auf dem Einheitskreis ausdrücken:

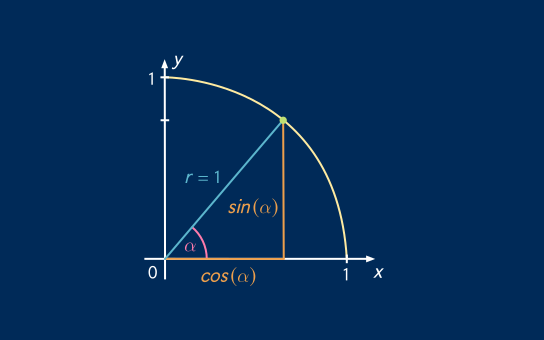
Die Sinusfunktion
Im ersten Quadranten des Koordinatensystems gilt für einen Punkt ![]() auf dem Einheitskreis: Der Sinus des Winkels
auf dem Einheitskreis: Der Sinus des Winkels ![]() zwischen der
zwischen der ![]() -Achse und der Strecke
-Achse und der Strecke ![]() ist die
ist die ![]() -Koordinate des Punkts und der Cosinus von
-Koordinate des Punkts und der Cosinus von ![]() ist die
ist die ![]() -Koordinate:
-Koordinate:

Diese Gleichungen ergeben sich aus der Definition des Sinus und Cosinus und der Tatsache, dass der Radius des Einheitskreises ![]() ist. Denn im ersten Quadranten sind die Werte der Koordinaten eines Punkts das Gleiche wie die Längen der Katheten in einem rechtwinkligen Dreieck mit dem spitzen Winkel
ist. Denn im ersten Quadranten sind die Werte der Koordinaten eines Punkts das Gleiche wie die Längen der Katheten in einem rechtwinkligen Dreieck mit dem spitzen Winkel ![]() .
.
Für Punkte des Einheitskreises in den anderen drei Quadranten ist der Sinus des Winkels ![]() zwischen der Strecke
zwischen der Strecke ![]() und der
und der ![]() -Achse zunächst nicht definiert. Denn dieser Winkel ist größer als
-Achse zunächst nicht definiert. Denn dieser Winkel ist größer als ![]() und ist daher kein Innenwinkel eines rechtwinkligen Dreiecks. Wir können aber die gleichen Gleichungen verwenden, um den Sinus und Cosinus zu definieren.
und ist daher kein Innenwinkel eines rechtwinkligen Dreiecks. Wir können aber die gleichen Gleichungen verwenden, um den Sinus und Cosinus zu definieren.
Wir verwenden also die Gleichung ![]() als Definition des Sinus eines Winkels
als Definition des Sinus eines Winkels ![]() zwischen
zwischen ![]() und
und ![]() . Hierbei ist wie zuvor
. Hierbei ist wie zuvor ![]() derjenige Punkt auf dem Einheitskreis, dessen Radius mit der
derjenige Punkt auf dem Einheitskreis, dessen Radius mit der ![]() -Achse den Winkel
-Achse den Winkel ![]() einschließt. Indem wir den gesamten Einheitskreis durchlaufen, können wir jedem Winkel
einschließt. Indem wir den gesamten Einheitskreis durchlaufen, können wir jedem Winkel ![]() zwischen
zwischen ![]() und
und ![]() einen Sinuswert
einen Sinuswert ![]() zuordnen. Die Werte von
zuordnen. Die Werte von ![]() liegen zwischen
liegen zwischen ![]() und
und ![]() , da der Punkt
, da der Punkt ![]() auf dem Einheitskreis liegt. Durch Abtragen aller dieser
auf dem Einheitskreis liegt. Durch Abtragen aller dieser ![]() -Werte als Funktionswerte des Sinus erhalten wir den Funktionsgraphen der Sinusfunktion:
-Werte als Funktionswerte des Sinus erhalten wir den Funktionsgraphen der Sinusfunktion:

Mit dem Sinus rechnen
Die Definition des Sinus eines spitzen Winkels ![]() in einem rechtwinkligen Dreieck lautet:
in einem rechtwinkligen Dreieck lautet:
![]()
Sind zwei der drei Größen ![]() ,
, ![]() und
und ![]() gegeben, können wir die Gleichung nach der gesuchten Größe auflösen und mithilfe eines Taschenrechners diese Größe berechnen. Wir schauen uns im Folgenden zwei typische Aufgaben dazu an:
gegeben, können wir die Gleichung nach der gesuchten Größe auflösen und mithilfe eines Taschenrechners diese Größe berechnen. Wir schauen uns im Folgenden zwei typische Aufgaben dazu an:
Berechnung mit dem Sinus und gegebener Hypotenuse
Die steilste Straße der Welt steigt in dem Winkel ![]() gegenüber einer ebenen Straße an. Wenn wir mit dem Fahrrad
gegenüber einer ebenen Straße an. Wenn wir mit dem Fahrrad ![]() auf dieser Straße fahren, wie viele Höhenmeter haben wir dann erklommen?
auf dieser Straße fahren, wie viele Höhenmeter haben wir dann erklommen?
Um die Frage zu beantworten, schauen wir uns ein passendes rechtwinkliges Dreieck an:
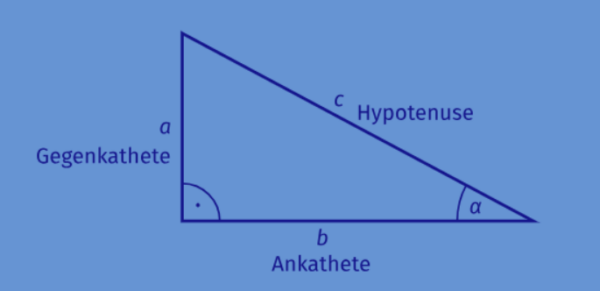
Der Steigungswinkel ist der Winkel ![]() . Die Straße verläuft entlang der Hypotenuse des Dreiecks. Die auf der Straße zurückgelegten
. Die Straße verläuft entlang der Hypotenuse des Dreiecks. Die auf der Straße zurückgelegten ![]() sind also die Länge der Hypotenuse:
sind also die Länge der Hypotenuse: ![]() . Gesucht ist die Höhe des Dreiecks, also die Länge der Gegenkathete
. Gesucht ist die Höhe des Dreiecks, also die Länge der Gegenkathete ![]() von
von ![]() . Für die Berechnung benutzen wir den Sinus von
. Für die Berechnung benutzen wir den Sinus von ![]() und gehen in folgenden Schritten vor:
und gehen in folgenden Schritten vor:
- Zuerst berechnen wir mit dem Taschenrechner den Sinus des Steigungswinkels:
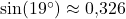 .
. - Als Nächstes lösen wir die Gleichung
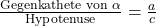 nach der gesuchten Gegenkathete auf und erhalten:
nach der gesuchten Gegenkathete auf und erhalten:  .
. - Setzen wir
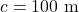 und
und 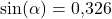 ein, erhalten wir die Länge der Gegenkathete:
ein, erhalten wir die Länge der Gegenkathete:  .
.
Auf einer Strecke von ![]() auf der Straße legen wir also
auf der Straße legen wir also ![]() Höhenmeter zurück.
Höhenmeter zurück.
Berechnung mit dem Sinus und gegebener Kathete
Von einem rechtwinkligen Dreieck ![]() kennen wir nur den Winkel
kennen wir nur den Winkel ![]() und die Länge
und die Länge ![]() der Gegenkathete dieses Winkels. Um das Dreieck mit Winkelmesser und Lineal zeichnen zu können, benötigen wir beispielsweise die Länge der Hypotenuse
der Gegenkathete dieses Winkels. Um das Dreieck mit Winkelmesser und Lineal zeichnen zu können, benötigen wir beispielsweise die Länge der Hypotenuse ![]() .
.
Wir können die Hypotenuse nicht mit dem Satz des Pythagoras berechnen, denn dazu bräuchten wir die Länge ![]() der zweiten Kathete. Wir gehen ähnlich vor wie im vorigen Beispiel:
der zweiten Kathete. Wir gehen ähnlich vor wie im vorigen Beispiel:
- Mit dem Taschenrechner berechnen wir
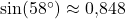 .
. - Wir lösen die Formel
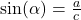 nach der gesuchten Größe
nach der gesuchten Größe  auf und erhalten:
auf und erhalten:  .
. - Wir setzen
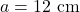 und
und  ein und erhalten:
ein und erhalten: 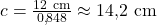 .
.
Häufig gestellte Fragen zum Thema Sinus