Rechnen mit den binomischen Formeln – Erklärung, Herleitung und Beispiele
Die binomischen Formeln sind wichtige Regeln in der Mathematik zur Umformung spezifischer Terme. Lerne, wie man Klammern auflöst und schnell multipliziert.
Inhaltsverzeichnis zum Thema Binomische Formeln
Teste dein Wissen
Wie viele binomische Formeln gibt es?
Frage 1 von 5
Was sind binomische Formeln?
Frage 2 von 5
Wie rechnet man binomische Formeln?
Frage 3 von 5
Was ist ein Binom?
Frage 4 von 5
Gibt es auch binomische Formeln hoch 3?
Frage 5 von 5
Binomische Formeln im Überblick
- Die binomischen Formeln sind in der Mathematik ein wichtiges Hilfsmittel bei Termumformungen, z. B. für Terme der Form
. - Du kannst mithilfe der binomischen Formeln Klammern auflösen. Es lohnt sich, die binomischen Formeln auswendig zu lernen, weil das Anwenden dieser schneller geht, als Klammern herkömmlich auszumultiplizieren.
- Es gibt drei binomische Formeln.
Die drei binomischen Formeln lassen sich geometrisch herleiten.
Quelle: sofatutor.com
Binomische Formeln – Einführung
Zunächst geben wir eine Übersicht über alle drei binomischen Formeln, bevor wir die Herleitung der binomischen Formeln erklären und uns Beispiele zum Rechnen mit den binomischen Formeln anschauen. Binomische Formeln heißen so, weil ein wesentlicher Bestandteil der Formeln sogenannte Binome sind. Ein Binom ist ein Term, der aus zwei Gliedern besteht, die durch ein Plus- oder Minuszeichen verknüpft sind, also zum Beispiel 
oder 
.
1. binomische Formel – Definition
Die erste binomische Formel lautet:
Die linke Seite der Gleichung ist das Produkt der Summe 
mit sich selbst. Sie lässt sich also auch schreiben als: 
2. binomische Formel – Definition
Die zweite binomische Formel lautet:
Die linke Seite der Gleichung ist das Produkt der Summe 
mit sich selbst. Sie lässt sich also auch schreiben als:
3. binomische Formel – Definition
Die dritte binomische Formel lautet:
Herleitung der binomischen Formeln
Die binomischen Formeln lassen sich sowohl algebraisch als auch geometrisch herleiten.
Algebraisch können wir die Klammern auf der linken Seite der binomischen Formeln mithilfe des Distributivgesetzes ausmultiplizieren.
Algebraische Herleitung der zweiten binomischen Formel
Da die Herleitung für alle drei binomischen Formeln recht ähnlich funktioniert, wird sie an dieser Stelle nur für die zweite binomische Formel ausführlich erklärt.
Wir betrachten dazu das Produkt 
. Wir multiplizieren jedes Element der linken Klammer mit jedem Element der rechten Klammer und fassen geschickt zusammen. Dabei achten wir auf die Vorzeichen:
Für die anderen beiden binomischen Formeln kannst du es ja mal selbst ausprobieren!
Binomische Formeln – geometrische Veranschaulichung
Wir können die binomischen Formeln grafisch darstellen und damit eine allgemeine Begründung für die Formeln finden. Dies schauen wir uns nun beispielhaft ebenfalls für die zweite binomische Formel an. Versuche es doch mal selbst mit den anderen beiden binomischen Formeln!
Geometrische Deutung der zweiten binomischen Formel
Für die geometrische Veranschaulichung der zweiten binomischen Formel betrachten wir ein Quadrat mit der Seitenlänge 
. Die Seitenlänge wird um 
verkleinert.
Dadurch ergibt sich ein verkleinertes Quadrat 
mit dem Flächeninhalt 
, das hier im Bild rot dargestellt ist:
Quelle sofatutor.com
Den Flächeninhalt können wir auch auf anderem Weg berechnen: Wir nehmen den Flächeninhalt des gesamten Quadrats, also 
, und ziehen davon die beiden Rechtecke mit dem Flächeninhalt 
ab. In dem Bild sind das die beiden grünen Rechtecke jeweils zusammen mit dem blauen Quadrat. Wir rechnen: 
. Das blaue Quadrat mit dem Flächeninhalt 
ziehen wir dadurch doppelt ab und müssen diesen Flächeninhalt deswegen wieder addieren, also 
. Diese Überlegungen fassen wir nun in einer mathematischen Formel zusammen und erhalten damit für den Flächeninhalt 
des roten Quadrates genau die zweite binomische Formel:
Binomische Formeln anwenden
Es gibt in der Mathematik vielfältige Anwendungsbeispiele für die binomischen Formeln. Hier schauen wir uns ein paar Fälle an.
Mit binomischen Formeln faktorisieren – Erklärung
Manchmal ist es für die Lösung einer Aufgabe hilfreich, einen mathematischen Term als Produkt zu schreiben, das nennt man Faktorisieren. Hierfür können die binomischen Formeln rückwärts angewendet werden. Als „rückwärts anwenden“ wird hier bezeichnet, wenn man einen Term in der Form der rechten Seite einer der binomischen Formeln vorliegen hat. Dieser kann dann durch die rechte Seite der Formel ersetzt werden, die ein Produkt ist. Da die binomischen Formeln jeweils eine Gleichung beschreiben, sind die beiden Seiten äquivalent. Auch wenn es üblich ist, sie in Formelsammlungen und Ähnlichem in der Form wie oben angegeben aufzuschreiben, gilt die Gleichheit stets in beide Richtungen.
Hier haben wir für alle drei binomischen Formeln Beispiele zusammengetragen, in denen der Term durch Anwendung der Umkehrung der entsprechenden Formel faktorisiert wird:
| 1. binomische Formel |
 |
| 2. binomische Formel |
 |
3. binomische Formel |
 |
Binomische Formeln und Funktionen
Beim Berechnen von Scheitelpunkten oder Nullstellen von quadratischen Funktionen können die binomischen Formeln helfen.
Die Gleichungen können mit einer quadratischen Ergänzung so umgeformt werden, dass die binomischen Formeln umgekehrt angewendet werden können. Damit lässt sich die quadratische Funktion auf die Scheitelpunktform 
bringen. Die Koordinaten des Scheitelpunkts 
können in dieser Form direkt abgelesen werden.
Für den Fall, dass der Funktionsterm einer quadratischen Funktion direkt der rechten Seite einer binomischen Formel entspricht oder durch das Ausklammern eines konstanten Faktors auf diese Form gebracht werden kann, lässt sich der Funktionsterm als Produkt schreiben. Dann können wir die Nullstellen der Funktion nach dem Satz vom Nullprodukt aus den Faktoren ablesen.
Geschicktes Rechnen mit binomischen Formeln
Bisher haben wir in diesem Text die binomischen Formeln vor allem für Terme mit Variablen eingesetzt, aber auch beim Rechnen mit Zahlen helfen die binomischen Formeln. Dazu formen wir Produkte, die wir nicht so einfach im Kopf ausrechnen können, so mit den binomischen Formeln um, dass wir einen Term erhalten, den wir leicht im Kopf ausrechnen können.
Beispiel:
Hier haben wir die Rechnung durch Anwendung der dritten binomischen Formel vereinfacht.
Auch beim Rechnen mit Wurzeltermen oder beim Kürzen von Brüchen können binomische Formeln helfen:
- Betrachten wir den Term
. Diesen Bruch möchten wir kürzen. Wir erkennen im Nenner die rechte Seite der dritten binomischen Formel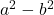 
. Wir können also den Nenner mithilfe der dritten binomischen Formel umwandeln und dann leicht kürzen:
- Wenn du in einem Term mit einer Wurzel die erste oder zweite binomische Formel erkennst, kannst du die Wurzel damit auflösen, die Erklärung folgt mit dieser Beispielrechnung:
Wir erzeugen hier zunächst unter der Wurzel ein Quadrat. Im letzten Schritt heben sich die Wurzel und das Quadrat dann gegenseitig auf.
Häufig gestellte Fragen zum Thema Binomische Formeln
Die binomischen Formeln sind Regeln, mit denen Terme, die eine bestimmte Form haben, umgeformt werden können.
Es gibt drei verschiedene binomische Formeln.
Die binomischen Formeln helfen beim Umformen von Termen, insbesondere beim Auflösen von Klammern. Umgekehrt können die binomischen Formeln beim Ausklammern helfen. Diese Anwendungen der binomischen Formeln können auch beim Lösen von Textaufgaben helfen. Das ist leider nicht immer offensichtlich, es lohnt sich also, längere Terme in Aufgaben auf (versteckte) binomische Formeln zu untersuchen.
Liegt ein Term schon in der Form einer Seite einer binomischen Formel vor, also z. B. in der Form 
, kann die Umformungsregel direkt angewendet werden. Sonst muss der Term zunächst noch in eine passende Form gebracht werden.
Die erste binomische Formel lautet:
Die binomischen Formeln sind Regeln, die beim Umformen von bestimmten Termen helfen. Wir können damit Terme schneller berechnen. Wenn wir in einem Term eine Seite der binomischen Formeln erkennen, wissen wir, dass wir sie anwenden können.
Beispiel für die zweite binomische Formel:
.1. binomische Formel:
2. binomische Formel:
3. binomische Formel: 
Mit den binomischen Formeln werden Terme berechnet, die eine bestimmte Form haben.
Die drei binomischen Formeln gelten für unterschiedliche Terme, die aber eine ähnliche Form haben.
Ein Binom ist ein Term, der aus zwei Gliedern besteht, die durch ein Plus- oder Minuszeichen verknüpft sind.
Beispiele:
Es gibt als allgemeine Formel den sogenannten binomischen Lehrsatz. Mit diesem können beliebige Potenzen von Binomen, also quasi binomische Formeln mit beliebigen Potenzen, berechnet werden.
Für die dritte Potenz gilt zum Beispiel:
Im pascalschen Dreieck wird der Binomialkoeffizient grafisch dargestellt. Der Binomialkoeffizient ist ein Bestandteil der Formel des binomischen Lehrsatzes. Als Sonderfall des binomischen Lehrsatzes für 
können die Koeffizienten der ersten beiden binomischen Formeln aus der zweiten Zeile des pascalschen Dreiecks abgelesen werden.
Steht bei einem Term ein Minus vor der Klammer, auf die die binomische Formel angewendet werden soll, wird erst die Umformung der binomischen Formel vorgenommen. Der Term wird dabei eingeklammert und am Ende das Minus verrechnet.
Beispiel:
