Schrägbild eines Körpers – einfach erklärt

Körper sind dreidimensionale geometrische Figuren. Sie besitzen eine sogenannte räumliche Tiefe (häufig als Breite bezeichnet). Wollen wir Körper zeichnen, müssen wir diesen räumlichen Effekt auf unserem zweidimensionalen Papier erzeugen. Das erreichen wir mit Verzerrungen und Verkürzungen. Das so entstandene Bild wird als Schrägbild bezeichnet. Schrägbilder dienen also zur Darstellung von geometrischen Körpern.
Die folgende Grafik zeigt das Schrägbild eines Würfels:

Das dreidimensionale Zeichnen von Schrägbildern gelingt, wenn wir Folgendes beachten:

• Die Vorderansicht (Aufriss) verändert sich nicht.
• Die Seiten- und Deckflächen sind verkürzt dargestellt, wodurch der räumliche Effekt erzeugt wird. 
• Die Seitenkanten des Körpers laufen schräg nach hinten und sind kürzer dargestellt.
• Parallele Kanten sind auch im Schrägbild parallel.
• Verdeckte Kanten werden meistens gestrichelt gezeichnet. 

Eine wichtige Rolle beim Zeichnen von Schrägbildern spielen der Verzerrungswinkel und der Verkürzungsfaktor.

Als Verzerrungswinkel wird der Winkel bezeichnet, mit dem die seitlichen Kanten eines Schrägbilds schräg nach hinten laufen. Je nach Größe des Winkels berechnet sich auch der Verkürzungsfaktor . Das ist der Faktor, mit dem die wirkliche Seitenlänge multipliziert wird, um die Länge der Seite in der Zeichnung zu erhalten.
Häufig beträgt . In diesem Fall ist der Verkürzungsfaktor .

Für ist .
Für ist .

Je größer der Verzerrungswinkel, desto kleiner ist der Verkürzungsfaktor.

Im folgenden Bild sind drei Schrägbilder des gleichen Würfels dargestellt. Der Verzerrungswinkel ist jedes Mal unterschiedlich groß. Somit unterscheidet sich auch der Verkürzungsfaktor:

Der Winkel ist der Winkel zwischen der vorderen Kante und der Kante, die schräg nach hinten verläuft.

Hat der dargestellte Würfel beispielsweise die Seitenlänge , haben die schräg nach hinten laufenden Kanten in den drei Bildern die folgenden Längen:

• :
• :
• :

Ist der Verzerrungswinkel in einer Aufgabe nicht vorgegeben, wird in den meisten Fällen von ausgegangen.

Im Folgenden ist Schritt für Schritt erklärt, wie das Schrägbild eines Quaders gezeichnet wird.
Es soll das Schrägbild eines Quaders mit der Länge , der Höhe und der Breite gezeichnet werden.

Schritt 1: Zunächst zeichnen wir die Vorderseite mit der Länge und der Höhe . Dabei muss noch keine Verzerrung beachtet werden.

Schritt 2: Im Anschluss zeichnen wir die schräg nach hinten gehenden Kanten. Dafür wählen wir den Verzerrungswinkel . Beim Verwenden von Kästchenpapier entspricht ein Winkel von den Diagonalen der Kästchen. An diesen können wir uns orientieren. Häufig wird auch eine Kästchendiagonale für eine Einheit nach hinten genutzt.
Arbeiten wir mit einem Verzerrungsfaktor, muss die Länge der Kanten berechnet werden. Sie ergibt sich als Produkt aus der eigentlichen Länge und dem Verkürzungsfaktor . Wir zeichnen die Kanten also mit einer Länge von ein.

Schritt 3: Im letzten Schritt werden die hinteren Kanten gezeichnet. Dabei verbinden wir die Endpunkte der nach hinten laufenden Kanten der Länge miteinander. Alle Linien, die von einer anderen Seite überdeckt werden, zeichnen wir nur gestrichelt ein.

Skizze: Es kann helfen, vor dem Zeichnen eines Schrägbilds eine Skizze anzufertigen. In der Skizze kann bereits geschaut werden, welche Kanten wie verlaufen und welche Ecken miteinander verbunden werden müssen.

Schrägbilder können von allen möglichen Körpern gezeichnet werden. Wie die Schrägbilder der gängigsten geometrischen Körper gezeichnet werden, schauen wir uns im Folgenden an.

Beim Zeichnen eines Würfel-Schrägbilds gehen wir genauso wie beim Zeichnen des Schrägbilds eines Quaders vor. 

• Schritt 1: Vorderseite zeichnen
• Schritt 2: Kanten, die nach hinten gehen, unter Beachtung des Verzerrungswinkels und des Verkürzungsfaktors oder als Kästchendiagonalen zeichnen
• Schritt 3: Hintere Kanten zeichnen, dabei auf verdeckte Kanten achten

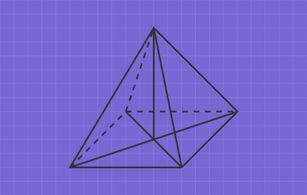
Beim Zeichnen des Schrägbilds einer quadratischen Pyramide gehen wir folgendermaßen vor:

• Schritt 1: Quadratische Grundfläche als Parallelogramm zeichnen. Nach hinten verlaufende Seiten unter Beachtung des Verzerrungswinkels und des Verkürzungsfaktors oder als Kästchendiagonalen zeichnen
• Schritt 2: Beide Diagonalen der Grundfläche einzeichnen, dafür die gegenüberliegenden Ecken miteinander verbinden
• Schritt 3: Vom Schnittpunkt der beiden Diagonalen eine Linie mit der Länge der Höhe nach oben einzeichnen. Am Ende der senkrechten Linie befindet sich die Spitze der Pyramide.
• Schritt 4: Eckpunkte der Grundfläche mit der Spitze verbinden

Um das Schrägbild eines Kreiszylinders zu zeichnen, gehen wir folgendermaßen vor:

• Schritt 1: Grundfläche als Ellipse zeichnen. Dafür den Durchmesser als horizontale Linie einzeichnen. Vom Mittelpunkt des Durchmessers eine Linie im gewünschten Verzerrungswinkel, hier 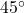, einzeichnen. Diese ist perspektivisch verkürzt und deshalb kürzer als der Durchmesser, und zwar entsprechend dem Verkürzungsfaktor 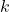. Endpunkte der beiden Diagonalen zu einer Ellipse verbinden
• Schritt 2: Höhe von den Enden der horizontalen Diagonalen nach oben zeichnen
• Schritt 3: Deckfläche analog zur Grundfläche konstruieren

Um das Schrägbild eines Prismas zu zeichnen, gehen wir folgendermaßen vor:

• Schritt 1: Zeichnen der Vorderseite (bei einem fünfeckigen Prisma ist die Vorderseite ein Fünfeck)
• Schritt 2: Nach hinten laufende Kanten zeichnen. Dabei immer auf den Verzerrungswinkel und den Verkürzungsfaktor achten bzw. Kästchendiagonalen nutzen
• Schritt 3: Die Enden der seitlichen Kanten so verbinden, dass die Rückseite entsteht

Beim Zeichnen des Schrägbilds eines Dreiecksprismas gehen wir analog vor, die Vorder- und Rückseite sind in diesem Fall Dreiecke.

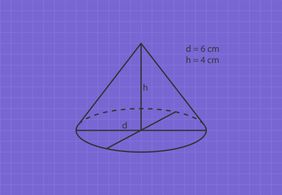
Um das Schrägbild eines Kreiskegels zu zeichnen, gehen wir folgendermaßen vor:

• Schritt 1: Grundfläche als Ellipse zeichnen. Dafür den Durchmesser als horizontale Linie einzeichnen. Vom Mittelpunkt des Durchmessers eine Linie im gewünschten Verzerrungswinkel, hier 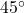, einzeichnen. Diese ist perspektivisch verkürzt und deshalb kürzer als der Durchmesser, und zwar entsprechend dem Verkürzungsfaktor 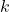. Endpunkte der beiden Diagonalen zu einer Ellipse verbinden
• Schritt 2: Die Spitze des Kegels liegt senkrecht über dem Schnittpunkt der beiden Durchmesserlinien. Die Höhe wird als senkrecht auf dem Schnittpunkt stehende Linie abgetragen.
• Schritt 3: Spitze mit den Endpunkten des horizontalen Durchmessers verbinden