Bedingte Wahrscheinlichkeit: Erklärung, Definition und Berechnung

Erfahre, wie bedingte Wahrscheinlichkeit das Eintreten eines Ereignisses unter einer gegebenen Bedingung beschreibt. Lerne, wie Baumdiagramme und Vierfeldertafeln genutzt werden, entdecke Rechenregeln und erkunde Beispiele zur Anwendung.

Inhaltsverzeichnis zum Thema Bedingte Wahrscheinlichkeit

Das Quiz zum Thema: Bedingte Wahrscheinlichkeit

Was ist die Definition einer bedingten Wahrscheinlichkeit?

Frage 1 von 5

Welches Werkzeug wird verwendet, um bedingte Wahrscheinlichkeiten visuell darzustellen?

Frage 2 von 5

Wie werden zwei Ereignisse A und B genannt, wenn P(A | B) = P(A)?

Frage 3 von 5

Welche Formel beschreibt die bedingte Wahrscheinlichkeit P(A | B)?

Frage 4 von 5

Was zeigt die Gegenwahrscheinlichkeit einer bedingten Wahrscheinlichkeit P(A | B)?

Frage 5 von 5

Bedingte Wahrscheinlichkeit im Überblick

  • Für die bedingte Wahrscheinlichkeit eines Ereignisses A mit der Bedingung B sind P(A \vert B) und P_B(A) übliche Schreibweisen.
  • In Mathe gibt eine bedingte Wahrscheinlichkeit an, wie wahrscheinlich das Eintreten eines Ereignisses unter der Bedingung ist, dass ein anderes Ereignis bereits eingetreten ist.
  • Zum Rechnen mit bedingten Wahrscheinlichkeiten können wir Baumdiagramme und Vierfeldertafeln nutzen.
  • Wenn sich die bedingte Wahrscheinlichkeit P(A \vert B) nicht von der Wahrscheinlichkeit P(A) unterscheidet, dann nennen wir zwei Ereignisse A und B unabhängig.
Bedingte Wahrscheinlichkeit: Lernvideo

Quelle sofatutor.com

Bedingte Wahrscheinlichkeit – Einführung

Wenn es in Stochastik um bedingte Wahrscheinlichkeiten geht, dann ist damit die Wahrscheinlichkeit gemeint, dass ein Ereignis A unter der Bedingung eintritt, dass ein anderes Ereignis B bereits eingetreten ist. 
Dafür schreiben wir: P(A \vert B) oder P_B(A) (sprich „P von A unter der Bedingung B“). 

Im Folgenden wird einfach erklärt, wie du bedingte Wahrscheinlichkeiten erkennen und berechnen kannst.

Bedingte Wahrscheinlichkeit – Baumdiagramm

Bei einem Baumdiagramm sind die Äste der zweiten Stufe stets mit bedingten Wahrscheinlichkeiten beschriftet, da hier bereits ein Ereignis in der ersten Stufe eingetreten ist. Das Ereignis der ersten Stufe eines Astes ist also die Bedingung unter der die Wahrscheinlichkeiten in der zweiten Stufe angegeben werden.

Baumdiagramm – Bedingte Wahrscheinlichkeit

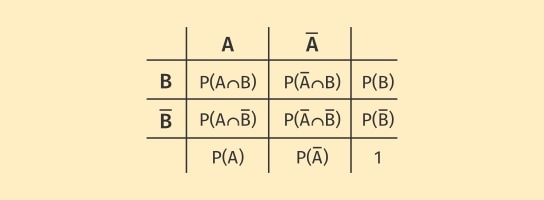
Bedingte Wahrscheinlichkeit – Vierfeldertafel

Eine Vierfeldertafel zeigt den Zusammenhang von zwei Ereignissen und den zugehörigen Gegenereignissen in Form der Schnittwahrscheinlichkeiten. Mit diesen Informationen können wir für die Ereignisse die bedingten Wahrscheinlichkeiten ausrechnen.

Vierfeldertafel

Bedingte Wahrscheinlichkeit – Definition

Eine bedingte Wahrscheinlichkeit P(A \vert B) bezeichnet die Wahrscheinlichkeit dafür, dass ein Ereignis A unter der Bedingung eintritt, dass ein anderes Ereignis B zuvor eingetreten ist.

Bedingte Wahrscheinlichkeit – Formel

Eine Formel für die bedingte Wahrscheinlichkeit kann direkt aus der ersten Pfadregel im Baumdiagramm abgeleitet werden. Danach ist die Wahrscheinlichkeit für einen Pfad gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades:
P(A \cap B) = P(B) \cdot P(A \vert B)
Eine Division durch P(B) liefert die Formel für die bedingte Wahrscheinlichkeit:
P(A \vert B) = \dfrac{P(A \cap B)}{P(B)}

Bedingte Wahrscheinlichkeit – Rechenregeln

Zwei Ereignisse A und B sind stochastisch unabhängig wenn gilt:
P(A \vert B) = P(A) und P(B \vert A) = P(B)

Bedingte Wahrscheinlichkeit und stochastische Unabhängigkeit

Durch Einsetzen der Formel für die bedingte Wahrscheinlichkeit erhalten wir den allgemeinen Zusammenhang:
\begin{array}{cccl} \dfrac{P(A \cap B)}{P(B)} & = & P(A) & \vert \cdot P(B) \\ P(A \cap B) & = & P(A) \cdot P(B) & \end{array}

Bedingte Wahrscheinlichkeit und Multiplikationssatz

Der Multiplikationssatz gibt an, wie die Schnittwahrscheinlichkeit P(A \cap B) berechnet werden kann. Die Rechnung entspricht der Anwendung der ersten Pfadregel im Baumdiagramm:
P(A \cap B) = P(B) \cdot P(A \vert B) = P(A) \cdot P(B \vert A)

Bedingte Wahrscheinlichkeit und totale Wahrscheinlichkeit

Die totale Wahrscheinlichkeit P(A) für ein Ereignis A kann als Summe von Schnittwahrscheinlichkeiten angegeben werden. Es gilt:
P(A) = P(A \cap B) + P(A \cap \bar{B})
Die Schnittwahrscheinlichkeiten können wir dafür über den Multiplikationssatz mit den bedingten Wahrscheinlichkeiten berechnen.

Bedingte Wahrscheinlichkeit und Gegenwahrscheinlichkeit

Die Gegenwahrscheinlichkeit, auch Komplement, einer bedingten Wahrscheinlichkeit P(A \vert B) ist die die Wahrscheinlichkeit des Gegenereignisses \bar{A} unter derselben Bedingung B. Dabei ist auch für eine bedingte Wahrscheinlichkeit die Summe mit ihrer Gegenwahrscheinlichkeit stets 1:
P(A \vert B) + P(\bar{A} \vert B) = 1

Bedingte Wahrscheinlichkeit – Beispiel

Betrachten wir ein Beispiel mit den folgenden Angaben:

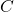  • C: Ein Haushalt besitzt einen Computer.
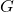  • G: Ein Haushalt verfügt über einen Glasfaseranschluss. 
  • P(C) = 80\,\%
  • P(G) = 15\,\%
  • P(C \cap G) = 14\,\%

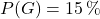
Wir wollen alle bedingten Wahrscheinlichkeiten bestimmen. Dazu erstellen wir zunächst eine Vierfeldertafel und füllen sie vollständig aus:

C \bar{C}
G \mathbf{14\,\%} 1\,\% \mathbf{15\,\%}
\bar{G} 66\,\% 19\,\% 85\,\%
\mathbf{80\,\%} 20\,\% 100\,\%

Damit können wir mit der allgemeinen Formel P(A \vert B) = \dfrac{P(A \cap B)}{P(B)} alle bedingten Wahrscheinlichkeiten berechnen, zudem können wir die Rechenregeln nutzen. Tabelle der bedingten Wahrscheinlichkeiten:

Berechnung Wert Beschreibung
P(C \vert G) \dfrac{P(C \cap G)}{P(G)} 93,3\,\% Ein Haushalt mit Glasfaseranschluss hat einen Computer.
P(C \vert \bar{G}) \dfrac{P(C \cap \bar{G})}{\bar{G}} 77,6\,\% Ein Haushalt ohne Glasfaseranschluss hat einen Computer.
P(\bar{C} \vert G) 1 - P(C \vert G) 6,7\,\% Ein Haushalt mit Glasfaseranschluss hat keinen Computer.
P(\bar{C} \vert \bar{G}) 1 - P(C \vert \bar{G}) 22,4\,\% Ein Haushalt ohne Glasfaseranschluss hat keinen Computer.
P(G \vert C) \dfrac{P(C \cap G)}{P(C)} 17,5\,\% Ein Haushalt mit Computer hat einen Glasfaseranschluss.
P(G \vert \bar{C}) \dfrac{P(\bar{C} \cap G)}{\bar{C}} 5\,\% Ein Haushalt ohne Computer hat einen Glasfaseranschluss.
P(\bar{G} \vert C) 1 - P(G \vert C) 82,5\,\% Ein Haushalt mit Computer hat keinen Glasfaseranschluss.
P(\bar{G} \vert \bar{C}) 1 - P(G \vert \bar{C}) 95\,\% Ein Haushalt ohne Computer hat keinen Glasfaseranschluss.

Häufige gestellte Fragen zu bedingten Wahrscheinlichkeiten

Eine bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit für das Eintreten eines Ereignisses A unter bestimmten Voraussetzungen, der sogenannten Bedingung B.
Mathematisch wird die Wahrscheinlichkeit für das Ereignis A unter der Bedingung B so geschrieben:
P_B(A) \quad oder \quad P(A \vert B).

Die bedingte Wahrscheinlichkeit kann mit der folgenden Formel berechnet werden:
P_B(A) = \dfrac{P(A \cap B)}{P(B)}

Eine bedingte Wahrscheinlichkeit ist dadurch charakterisiert, dass das Eintreten der Bedingung als bereits bekannt vorausgesetzt ist. In einer Aufgabe erkennst du sie daran, dass eines der Ereignisse bereits festgelegt ist.

Die Bedingung ist bei einer bedingten Wahrscheinlichkeit das Ereignis, das bereits eingetreten ist und als Voraussetzung dient.

In einem Baumdiagramm stehen an den Ästen der zweiten Stufe bedingte Wahrscheinlichkeiten, da hier in der ersten Stufe bereits ein Ereignis eingetreten ist.

Wahrscheinlichkeiten können unter verschiedenen Bedingungen betrachtet werden. Zum Beispiel enthält ein mehrstufiges Baumdiagramm zum Ziehen ohne Zurücklegen an den Ästen Wahrscheinlichkeiten für das Eintreten bestimmter Ereignisse unter der Bedingung, dass zuvor mehrere bestimmte Ereignisse eingetreten sind.

Der Satz von Bayes gibt an, wie eine bedingte Wahrscheinlichkeit P(A \vert B) ohne Verwendung der Schnittwahrscheinlichkeit aus den Wahrscheinlichkeiten der Ereignisse A und B sowie der bedingten Wahrscheinlichkeit P(B \vert A) berechnet werden kann.
Es gilt:
P(A \vert B) = \dfrac{P(B \vert A) \cdot P(A)}{P(B)}

Die totale Wahrscheinlichkeit gibt an, mit welcher Wahrscheinlichkeit ein Ereignis eintritt, wenn sonst nichts bekannt ist. Eine bedingte Wahrscheinlichkeit gibt die Wahrscheinlichkeit für das Eintreten eines Ereignisses unter bestimmten, bekannten Voraussetzungen (der sogenannten Bedingung) an.

Eine bedingte Wahrscheinlichkeit setzt voraus, dass die Bedingung bereits eingetreten ist. Es ist die Wahrscheinlichkeit für das Auftreten eines Ereignisses unter diesen Voraussetzungen. Eine unbedingte (totale) Wahrscheinlichkeit gibt die Wahrscheinlichkeit für das Auftreten des Ereignisses ohne Vorkenntnisse an.

Um den Erwartungswert einer Zufallsgröße zu berechnen, werden die Ausprägungen der Zufallsgröße und ihre Wahrscheinlichkeiten benötigt. Diese können auch mithilfe bedingter Wahrscheinlichkeiten berechnet werden:
P(A \cap B) = P(B) \cdot P(A \vert B)

Je nach Fragestellung können wir für Zufallsvariablen bedingte Wahrscheinlichkeiten berechnen. Dabei kannst du bedingte Wahrscheinlichkeiten an einer Fragestellung erkennen, bei der das Eintreten eines Ereignisses als gegeben oder bekannt vorausgesetzt wird. Das bereits sicher eingetretene Ereignis ist dabei die Bedingung.

Super! Das Thema: kannst du schon! Teile deine Learnings und Fragen mit der Community!

Alle Artikel aus dem Fach Mathematik