Trigonometrische Funktionen – Übersicht
Erfahre, wie trigonometrische Funktionen den Zusammenhang zwischen Winkeln und Seitenverhältnissen in Dreiecken beschreiben. Die Sinus-, Cosinus- und Tangensfunktionen sind hier die Hauptakteure. Lerne mehr über Eigenschaften, Ableitungen, Verschiebungen und das Zeichnen von trigonometrischen Funktionen!
Inhaltsverzeichnis zum Thema Trigonometrische Funktionen
Das Quiz zum Thema: Trigonometrische Funktionen
Was beschreiben die trigonometrischen Funktionen in rechtwinkligen Dreiecken?
Frage 1 von 5
Welche sind die drei wichtigsten trigonometrischen Funktionen?
Frage 2 von 5
Was beschreiben die trigonometrischen Funktionen in den Naturwissenschaften?
Frage 3 von 5
Welche Funktion beschreibt den Quotienten aus Sinus und Cosinus?
Frage 4 von 5
Welche Symmetrie besitzt die Cosinusfunktion?
Frage 5 von 5
Wie willst du heute lernen?
Trigonometrische Funktionen – einfach erklärt
Die trigonometrischen Funktionen (auch Winkelfunktionen oder Kreisfunktionen genannt) beschreiben den Zusammenhang zwischen Längenverhältnissen und Winkeln in rechtwinkligen Dreiecken. Sie können als Längen im Einheitskreis veranschaulicht werden. Dabei wird der Winkel häufig durch die zugehörige Bogenlänge angegeben.
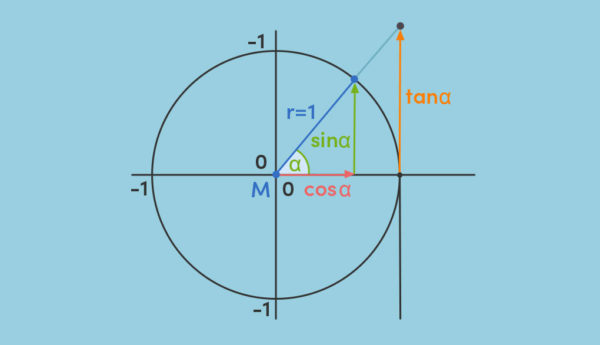
Die trigonometrischen Funktionen sind in den Naturwissenschaften die grundlegenden Funktionen, um periodische Vorgänge zu beschreiben.
Die drei wichtigsten trigonometrischen Funktionen sind die Sinusfunktion, die Cosinusfunktion und die Tangensfunktion.
In einem rechtwinkligen Dreieck mit den drei Winkeln ![]() ,
, ![]() und
und ![]() (
(![]() ) lauten die Formeln für die trigonometrischen Funktionen:
) lauten die Formeln für die trigonometrischen Funktionen:
![]()
![]()
![]()
![]()
![]()
![]()

Trigonometrische Funktionen – Eigenschaften
Die trigonometrischen Funktionen sind durch bestimmte Eigenschaften charakterisiert. Im Folgenden werden Periode, Definitions– und Wertebereich sowie Nullstellen und die Symmetrie der trigonometrischen Funktionen genannt.
Im Rahmen einer Kurvendiskussion können zusätzlich noch die Extremstellen, die Monotonie, die Wendepunkte und das Krümmungsverhalten der trigonometrischen Funktionen anhand der Ableitung bestimmt werden.
Sinusfunktion
Die wichtigsten Eigenschaften der Sinusfunktion ![]() sind:
sind:
- Periode:
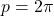
- Definitionsbereich:
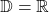
- Wertebereich:
![Rendered by QuickLaTeX.com \mathbb{W} = \bigl[ -1; 1 \bigr]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-d80804c856f668e4c5abd88c68244380_l3.png)
- Schnittpunkt mit der
 -Achse:
-Achse: 
- Nullstellen:
 mit
mit 
- Symmetrie: punktsymmetrisch zum Ursprung (
 )
) - Allgemeine Form:
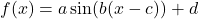

Cosinusfunktion
Die wichtigsten Eigenschaften der Cosinusfunktion ![]() sind:
sind:
- Periode:
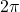
- Definitionsbereich:
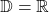
- Wertebereich:
![Rendered by QuickLaTeX.com \mathbb{W} = \bigl[ -1; 1 \bigr]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-d80804c856f668e4c5abd88c68244380_l3.png)
- Schnittpunkt mit der
 -Achse:
-Achse: 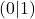
- Nullstellen:
 mit
mit 
- Symmetrie: achsensymmetrisch zum Ursprung (
 )
) - Allgemeine Form:


Tangensfunktion
Die wichtigsten Eigenschaften der Tangensfunktion ![]() sind:
sind:
- Periode:
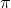
- Definitionsbereich:

- Wertebereich:

- Nullstellen:
 mit
mit 
- Symmetrie: punktsymmetrisch zum Ursprung (
 )
)
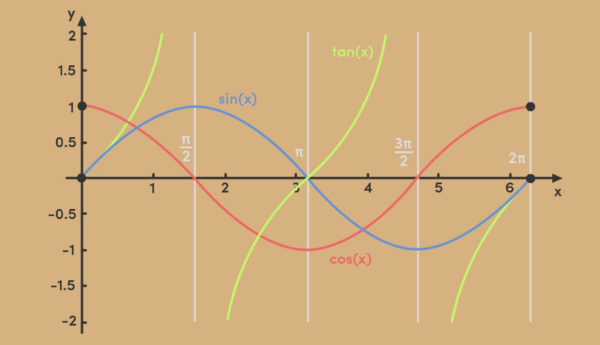
Der Tangens entspricht dem Quotienten aus Sinus und Cosinus:
![]()
Trigonometrische Funktionen verschieben
Die Parameter ![]() und
und ![]() in der allgemeinen Form der Funktionsgleichung sorgen für eine Verschiebung des Funktionsgraphen. Dabei gilt:
in der allgemeinen Form der Funktionsgleichung sorgen für eine Verschiebung des Funktionsgraphen. Dabei gilt:
- Wenn
 positiv ist, wird der Graph nach links verschoben.
positiv ist, wird der Graph nach links verschoben. - Wenn
 negativ ist, wird der Graph nach rechts verschoben.
negativ ist, wird der Graph nach rechts verschoben. - Wenn
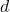 positiv ist, wird der Graph nach oben verschoben.
positiv ist, wird der Graph nach oben verschoben. - Wenn
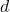 negativ ist, wird der Graph nach unten verschoben.
negativ ist, wird der Graph nach unten verschoben.
Hinweis: Durch eine Verschiebung nach links oder rechts können die Graphen der Sinus- und Cosinusfunktion direkt aufeinander abgebildet werden. Es kann also jede Sinusfunktion durch eine entsprechend verschobene Cosinusfunktion dargestellt werden und umgekehrt.
Zudem werden die Graphen aller trigonometrischen Funktionen durch eine Verschiebung um ein Vielfaches der Periodenlänge stets wieder auf sich selbst abgebildet, da sich die Funktionswerte periodisch wiederholen.
Die Parameter ![]() und
und ![]() bewirken eine Streckung oder Stauchung des Funktionsgraphen.
bewirken eine Streckung oder Stauchung des Funktionsgraphen.
Ableitungen trigonometrischer Funktionen
Für die Ableitungen der Sinus- und Cosinusfunktion gilt:
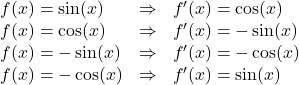
Die Ableitung des Tangens ist etwas komplizierter:
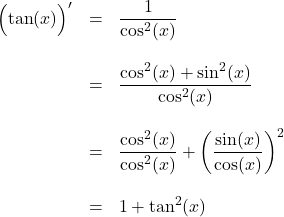
Auch über die Quotientenregel kann die Ableitung des Tangens bestimmt werden, da er der Quotient aus Sinus und Cosinus ist:
![]()
Hier wurde jeweils der Zusammenhang, dass die Summe aus dem Sinus ins Quadrat und dem Cosinus ins Quadrat immer ![]() ergibt, verwendet:
ergibt, verwendet:
![]()
Rechnen mit trigonometrischen Funktionen
Beim Lösen von Aufgaben zu trigonometrischen Funktionen mit dem Taschenrechner muss beachtet werden, ob die Winkel in Grad oder im Bogenmaß gegeben oder gefragt sind. Das Bogenmaß ist dabei das Verhältnis zwischen der Bogenlänge, die ein Winkel umfasst, und dem Radius eines Kreises. Im Taschenrechner sind diese beiden Einheiten abgekürzt mit ![]() (Grad) und
(Grad) und ![]() (Bogenmaß).
(Bogenmaß).
Dabei entspricht ein voller Kreis einem Winkel von ![]() sowie einer Bogenlänge von
sowie einer Bogenlänge von ![]() .
.
Trigonometrische Funktionen bestimmen
Ist nicht vorgegeben, ob es sich um eine Sinus- oder Cosinusfunktion handelt, kannst du frei wählen, ob du von Sinus oder Cosinus ausgehen willst. Im Anschluss werden die Parameter der Funktion bestimmt.
Allgemeine Form beim Sinus: ![]()
- Parameter
 : halbe Differenz der
: halbe Differenz der  -Koordinaten der Hoch- und Tiefpunkte
-Koordinaten der Hoch- und Tiefpunkte - Parameter
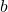 :
:  mit Periodenlänge
mit Periodenlänge 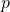 (Abstand zwischen zwei benachbarten Hoch- oder zwei benachbarten Tiefpunkten)
(Abstand zwischen zwei benachbarten Hoch- oder zwei benachbarten Tiefpunkten) - Parameter
 : Phasenverschiebung (Abstand des ersten Wendepunkts (Sinusfunktion) oder Hochpunkts (Cosinusfunktion) zu
: Phasenverschiebung (Abstand des ersten Wendepunkts (Sinusfunktion) oder Hochpunkts (Cosinusfunktion) zu 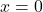 ) in
) in  -Richtung
-Richtung - Parameter
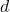 : Verschiebung der Funktion in
: Verschiebung der Funktion in  -Richtung
-Richtung
Der Funktionsterm der trigonometrischen Funktion wird aufgestellt, indem die bestimmten Werte für die Parameter in die allgemeine Form der Funktionsgleichung eingesetzt werden.
Trigonometrische Funktionen zeichnen
Eine trigonometrische Funktion lässt sich am besten zeichnen, indem zunächst die charakteristischen Punkte der Funktion zusammengetragen werden. Wichtige Punkte sind:
- der Schnittpunkt mit der
 -Achse,
-Achse, - die Nullstellen,
- die Hoch- und Tiefpunkte.
Um diese Punkte korrekt zu bestimmen, ist es wichtig, die Periode und die Amplitude der Funktion zu kennen.
Sind alle diese Eigenschaften der Funktion bestimmt, können die charakteristischen Punkte im Koordinatensystem eingezeichnet und zu einem Funktionsgraphen verbunden werden. Schauen wir uns dafür die folgende Beispielfunktion an:
![]()
Wir lesen daraus für die einzelnen Parameter ab:

Mit einer Verschiebung des Graphen verschieben sich auch der Schnittpunkt mit der ![]() -Achse, die Nullstellen und die Hoch- und Tiefpunkte. Die folgende Tabelle gibt die charakteristischen Punkte dieser trigonometrischen Funktion im Intervall
-Achse, die Nullstellen und die Hoch- und Tiefpunkte. Die folgende Tabelle gibt die charakteristischen Punkte dieser trigonometrischen Funktion im Intervall ![]() an.
an.
| Schnittpunkt mit der |
|
| Nullstellen | |
| Hochpunkte | |
| Tiefpunkte |
Diese Punkte können nun im Koordinatensystem markiert und zum Graph der Funktion verbunden werden.
Wichtig: Bei Tangensfunktionen müssen die Definitionslücken beachtet werden. An diesen Stellen hat der Graph der Funktion senkrechte Asymptoten. Eine Tangensfunktion der Form ![]() ist unter anderem an den Stellen
ist unter anderem an den Stellen ![]() und
und ![]() nicht definiert. Das bedeutet, bei diesen
nicht definiert. Das bedeutet, bei diesen ![]() -Werten kann eine senkrechte Linie als Hilfslinie eingezeichnet werden. Der Graph der Tangensfunktion nähert sich dieser Hilfslinie nur an, berührt sie jedoch nicht. Der Graph einer Tangensfunktion ist also keine durchgehende Linie.
-Werten kann eine senkrechte Linie als Hilfslinie eingezeichnet werden. Der Graph der Tangensfunktion nähert sich dieser Hilfslinie nur an, berührt sie jedoch nicht. Der Graph einer Tangensfunktion ist also keine durchgehende Linie.
Häufig gestellte Fragen zum Thema Trigonometrische Funktionen









Alle Artikel aus dem Fach Physik