Formel umstellen einfach erklärt mit Regeln und Beispielen

Entdecke, wie man Formeln in Mathe und Physik richtig umstellt, um gesuchte Größen zu berechnen. Erfahre, welche Äquivalenzumformungen nötig sind und wie Regeln wie die „Punkt-vor-Strich“-Regel angewendet werden.

Inhaltsverzeichnis zum Thema Formel umstellen

Formel umstellen im Überblick

  • Formeln müssen nicht nur in Mathe, sondern beispielsweise auch in Physik umgestellt werden, um die gesuchte Größe berechnen zu können.
  • Um Formel umzustellen, werden sogenannte Äquivalenzumformungen genutzt.
  • Alle Umformungen müssen gleichermaßen auf beiden Seiten der Formel durchgeführt werden.
Formel umstellen: Lernvideo

Quelle sofatutor.com

Quelle sofatutor.com

Was ist eine Formel?

Formeln sind sowohl in Mathematik als auch in Physik oder in Chemie von wichtiger Bedeutung. Sie geben einen Zusammenhang zwischen verschiedenen Größen an, etwa die Formel: F=m\cdot a. Die Kraft F, die auf einen Körper wirkt, entspricht dem Produkt aus seiner Masse m und Beschleunigung a.
Weitere Beispiele für Formeln sind die pq-Formel zum Lösen quadratischer Gleichungen in Mathe und das ohmsche Gesetz oder der Wirkungsgrad in Physik.
Damit eine in einer mathematischen Formel enthaltene Größe berechnet werden kann, muss die Formel häufig nach der gesuchten Größe aufgelöst werden. Dann können die gegebenen Werte eingesetzt und das Ergebnis berechnet werden.
Wird in der Kraftformel die Masse m gesucht, muss zunächst das a auf die andere Seite gebracht werden, sodass m allein auf einer Seite der Formel steht. Wie das funktioniert, schauen wir uns im nächsten Abschnitt an.

Formeln richtig umstellen

Zur Umstellung von Formeln werden sogenannte Äquivalenzumformungen benötigt. Diese Umformungen lassen die Lösung der Gleichung unverändert.
Damit stellen wir sicher, dass bei den Umformungen die Aussage der Formel nicht verändert wird. Erlaubt sind, neben den vier Grundrechenarten Addition, Subtraktion, Multiplikation und Division, beispielsweise auch das Wurzelziehen.
Beim Umstellen von Formeln müssen wir zudem die folgenden Regeln beachten:

  • Umformungsschritte müssen immer auf beiden Seiten durchgeführt werden.
  • Die „Punkt-vor-Strich-Regel“ muss beachtet werden, also zuerst die Multiplikation/Division und dann erst die Addition/Subtraktion durchführen.
  • Durch 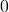0 darf nicht geteilt werden.

Das Umstellen von Formeln durch Äquivalenzumformungen wird in den folgenden Beispielen mit dem Äquivalenzzeichen, a = b ~\Leftrightarrow~ b = a, gekennzeichnet.

Formelumstellung – Beispiele

Betrachten wir zunächst unser Beispiel der Kraftformel F=m\cdot a von oben.
Wenn die Masse m bei gegebener Kraft F und Beschleunigung a gesucht ist, muss die Formel nach der Masse m umgestellt werden. Dazu muss die Beschleunigung a auf die linke Seite gebracht werden. Es gilt, zu überlegen, was wir rechnen müssen, damit a auf der rechten Seite verschwindet. Dies geschieht, indem wir beide Seiten durch a teilen:
\begin{array}{lrcll} &F&=&m\cdot a & \vert :a \\ \Leftrightarrow &\dfrac{F}{a} &=& m & \end{array}
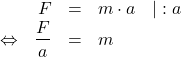
Wir haben die Formel durch die Äquivalenzumformung \vert : a nach der gesuchten Größe m umgestellt.

Formel mit Klammer umstellen 

Gelegentlich müssen zunächst Terme vereinfacht und Klammern aufgelöst werden, bevor die Formel umgestellt werden kann.
Beispiel:
\dfrac{a}{y}\cdot(y^2 +y\cdot d) = b soll nach y umgestellt werden.
Wir vereinfachen zunächst die linke Seite:
\begin{array}{lcll} \dfrac{a}{y}\cdot(y^2 +y d) &=& b &\vert \text{Klammer ausmultiplizieren}\\ \dfrac{a}{y} \cdot y^2 + \dfrac{a}{y} \cdot y d &= b & \vert \text{Kürzen} \\ ay + ad &= b &\vert a~\text{ausklammern} \\ a\cdot (y+d) &=b & \end{array}
Nun müssen wir a und d auf die rechte Seite bringen, damit y allein steht:
\begin{array}{llcll} &a\cdot (y+d) &=& b & \vert :a \\ \Leftrightarrow &y+d &=& \dfrac{b}{a} &\vert -d\\ \Leftrightarrow &y &=& \dfrac{b}{a} - d & \end{array}
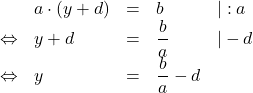
So erhalten wir eine Formel, um die gesuchte Größe y zu berechnen.

Formel mit Bruch umstellen

Eine bekannte Formel in der Physik, die als Bruch gegeben ist, ist die Geschwindigkeitsformel v=\frac{s}{t}. Die Geschwindigkeit berechnet sich also als Strecke pro Zeit. Ist die Geschwindigkeit zu 10~\frac{\text{m}}{\text{s}} und Zeit mit 2~\text{s} gegeben und wir wollen die zurückgelegte Strecke wissen, muss die Formel nach s umgestellt werden:
\begin{array}{llll} & v &=\dfrac{s}{t} &\vert \cdot t \\ \Leftrightarrow & v\cdot t &= s & \end{array}
Die Strecke berechnet sich also aus dem Produkt aus Geschwindigkeit und Zeit.
Die gegebenen Werte eingesetzt führen zu:
s = 10~\frac{\text{m}}{\text{s}} \cdot 2~\text{s} = 20~\text{m}

Formel mit Wurzel umstellen

Um eine Wurzel zu eliminieren, muss potenziert werden. Bei einer quadratischen Wurzel bedeutet dies auf beiden Seiten \uparrow^2. Bei einer Wurzel \sqrt[n]{x} muss mit dem Wurzelexponenten n potenziert werden.
Betrachten wir die Formel c = \sqrt{a\cdot b}. Diese soll nach a aufgelöst werden:
\begin{array}{llll} & c &= \sqrt{a\cdot b} &\vert \uparrow^2\\ \Leftrightarrow & c^2 &= a\cdot b &\vert : b \\ \Leftrightarrow & \frac{c^2}{b} &= a& \end{array}

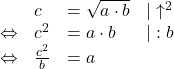
Häufig gestellte Fragen zum Thema Formel umstellen

Das Ziel ist, dass die gesuchte Variable allein auf einer Seite der Gleichung steht. Formeln werden mithilfe von Äquivalenzumformungen umgestellt. Dabei müssen alle Rechenschritte gleichermaßen auf beiden Seiten der Gleichung ausgeführt werden. Du darfst addieren, subtrahieren, multiplizieren, dividieren, quadrieren oder auch Wurzeln ziehen.

Um eine Formel umzustellen, müssen Äquivalenzumformungen durchgeführt werden. Dies bedeutet, dass auf beiden Seiten der Formel die gleichen Rechenschritte durchgeführt werden müssen. Das können die Grundrechenarten oder auch das Wurzelziehen sein.

Das Ziel der Formelumstellung ist, die gesuchte Variable zu isolieren. Dazu werden entsprechende Äquivalenzumformungen gemacht, also alle Rechenschritte auf beiden Seiten der Gleichungen durchgeführt. 

Wenn die Gleichung einen Bruch enthält und der Nenner dieses Bruchs auf die andere Seite gebracht werden soll, muss man mit diesem Nenner multiplizieren. 

Zwei Flaschen kosten 10€. Es wurden 30€ ausgegeben. Die Frage ist, wie viele Flaschen gekauft wurden. Dazu kannst du folgende Dreisatzformel aufstellen und umstellen:
\dfrac{2}{10} = \dfrac{x}{30}
x steht für die Anzahl an Flaschen. Das Verhältnis links von 2 zu 10 muss das gleiche sein wie x zu 30.
Nun kann mit 30 multipliziert werden, damit x allein steht:
x = 30\cdot \dfrac{2}{10} = \dfrac{60}{10} = 6
Es wurden also sechs Flaschen gekauft.

Leave A Comment

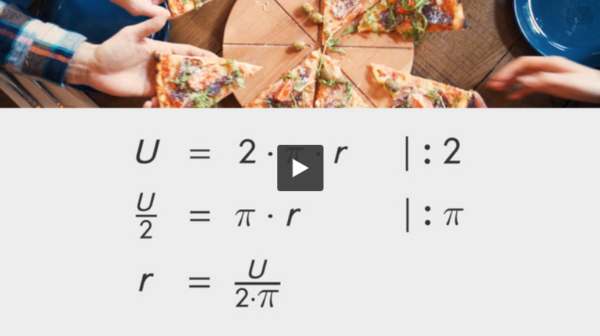
Alle Artikel aus dem Fach Mathematik