Vierfeldertafel – Definition und Beispiele
Die Vierfeldertafel verknüpft zwei Merkmale mit je zwei Ausprägungen und zeigt absolute oder relative Häufigkeiten. Erfahre, wie sie bedingte Wahrscheinlichkeit und stochastische Unabhängigkeit darstellt.
Inhaltsverzeichnis zum Thema Vierfeldertafel
Das Quiz zum Thema: Vierfeldertafel
Was ist eine Vierfeldertafel?
Frage 1 von 5
Wofür wird eine Vierfeldertafel verwendet?
Frage 2 von 5
Wie rechnet man mit einer Vierfeldertafel?
Frage 3 von 5
Wann benutzt man eine Vierfeldertafel?
Frage 4 von 5
Was zeigt eine Vierfeldertafel?
Frage 5 von 5
Wie willst du heute lernen?
Vierfeldertafel – Definition
Vierfeldertafeln werden in Mathe in der Stochastik (Wahrscheinlichkeitsrechnung) verwendet. Sie stellen Wahrscheinlichkeiten, absolute oder relative Häufigkeiten in einer Tabelle dar. Dabei hat eine Vierfeldertafel immer denselben Aufbau: Durch die Und-Verknüpfung von zwei Merkmalen mit je zwei Merkmalsausprägungen entstehen die vier inneren Felder, die namensgebend sind.

Wie in der Darstellung werden die beiden ersten Merkmalsausprägungen ![]() und
und ![]() , sprich „nicht
, sprich „nicht ![]() “, über die vier inneren Felder geschrieben. Die beiden Ausprägungen
“, über die vier inneren Felder geschrieben. Die beiden Ausprägungen ![]() und
und ![]() stehen auf der linken Seite neben den Feldern. In den inneren Feldern stehen die Verknüpfungen der Merkmalsausprägungen, also zum Beispiel im inneren Feld oben links
stehen auf der linken Seite neben den Feldern. In den inneren Feldern stehen die Verknüpfungen der Merkmalsausprägungen, also zum Beispiel im inneren Feld oben links ![]() und
und ![]() .
.
Einfach erklärt ist eine Vierfeldertafel also eine Tabelle, die das Eintreten oder Nichteintreten von zwei Ereignissen verknüpft. Dabei können in den Feldern die absoluten oder die relativen Häufigkeiten der kombinierten Ereignisse stehen. Die Felder am Ende einer Zeile bzw. am Ende einer Spalte enthalten stets die Summe der inneren Felder, die neben bzw. über dem Feld stehen.

Vierfeldertafel – absolute Häufigkeit
Wenn wir eine Vierfeldertafel erstellen, beginnen wir oft mit der absoluten Häufigkeit. Sie gibt die Anzahl der Objekte an, auf die ein Merkmal oder eine Kombination von Merkmalen zutrifft.
Die folgende Vierfeldertafel zeigt die absoluten Häufigkeiten von Schülerinnen und Schülern einer Jahrgangsstufe, die gerne schwimmen ![]() und gerne Rad fahren
und gerne Rad fahren ![]() .
.

Im äußeren Feld ganz unten rechts können wir ablesen, dass insgesamt ![]() Kinder die Jahrgangsstufe besuchen. An den äußeren Feldern können wir beispielsweise erkennen, dass insgesamt
Kinder die Jahrgangsstufe besuchen. An den äußeren Feldern können wir beispielsweise erkennen, dass insgesamt ![]() Schülerinnen und Schüler gerne Rad fahren oder dass
Schülerinnen und Schüler gerne Rad fahren oder dass ![]() nicht gerne schwimmen. Die inneren Felder enthalten die Zahlen der Schülerinnen und Schüler, auf die mehrere Merkmalsausprägungen gleichzeitig zutreffen. So gibt es in der Jahrgangsstufe zum Beispiel
nicht gerne schwimmen. Die inneren Felder enthalten die Zahlen der Schülerinnen und Schüler, auf die mehrere Merkmalsausprägungen gleichzeitig zutreffen. So gibt es in der Jahrgangsstufe zum Beispiel ![]() Kinder, die gerne schwimmen und Rad fahren, aber nur
Kinder, die gerne schwimmen und Rad fahren, aber nur ![]() Kinder, die gerne schwimmen und nicht gerne Rad fahren.
Kinder, die gerne schwimmen und nicht gerne Rad fahren.
Vierfeldertafel – relative Häufigkeit
Aus einer Vierfeldertafel mit relativen Häufigkeiten können wir auch die Wahrscheinlichkeiten dafür ablesen, dass bei zufälliger Auswahl eine entsprechende Merkmalskombination auftritt. Wir berechnen die relativen Häufigkeiten für die Vierfeldertafel, indem wir die absoluten Häufigkeiten durch die Gesamtzahl im Feld unten rechts teilen.
Dazu betrachten wir erneut das Beispiel von oben.

Dabei können Einträge als Brüche, Dezimalzahlen oder Prozentangaben erfolgen.

Wenn in der Vierfeldertafel relative Häufigkeiten angegeben sind, steht im Feld ganz unten rechts immer eine ![]() bzw.
bzw. ![]() . Aus der Vierfeldertafel können wir jetzt beispielsweise ablesen, dass die Wahrscheinlichkeit, dass ein zufällig ausgewählter Schüler nicht gerne schwimmt,
. Aus der Vierfeldertafel können wir jetzt beispielsweise ablesen, dass die Wahrscheinlichkeit, dass ein zufällig ausgewählter Schüler nicht gerne schwimmt, ![]() beträgt (äußeres Feld unter
beträgt (äußeres Feld unter ![]() ). Die Wahrscheinlichkeit, zufällig ein Kind zu erwischen, das gerne schwimmt und mit dem Fahrrad fährt, ist
). Die Wahrscheinlichkeit, zufällig ein Kind zu erwischen, das gerne schwimmt und mit dem Fahrrad fährt, ist ![]() (inneres Feld oben links).
(inneres Feld oben links).
Vierfeldertafel, bedingte Wahrscheinlichkeit und stochastische Unabhängigkeit
Eine Vierfeldertafel ermöglicht auch einfache Auswertungen in der Statistik. Wir können beispielsweise anhand der in einer Vierfeldertafel veranschaulichten Daten bedingte Wahrscheinlichkeiten berechnen oder die stochastische Unabhängigkeit der betrachteten Merkmale prüfen. Wir wollen dies nun allgemein an einer Vierfeldertafel mit den relativen Häufigkeiten der Ereignisse ![]() und
und ![]() betrachten. Dabei steht das Symbol
betrachten. Dabei steht das Symbol ![]() für die Schnittmenge, die der Und-Verknüpfung, also dem gleichzeitigen Eintreten, von zwei Ereignissen entspricht.
für die Schnittmenge, die der Und-Verknüpfung, also dem gleichzeitigen Eintreten, von zwei Ereignissen entspricht.

Bedingte Wahrscheinlichkeit:
Für die Wahrscheinlichkeit, dass ein Ereignis ![]() unter der Bedingung eintritt, wenn das Ereignis
unter der Bedingung eintritt, wenn das Ereignis ![]() bereits eingetreten ist, schreiben wir:
bereits eingetreten ist, schreiben wir: ![]() , sprich „
, sprich „![]() von
von ![]() unter der Bedingung
unter der Bedingung ![]() “.
“.
Zur Berechnung nutzen wir die Formel:
![]()
Die Vierfeldertafel enthält bereits alle Wahrscheinlichkeiten, die für die Formel benötigt werden, diese können also direkt eingesetzt werden.
Stochastische Unabhängigkeit:
Zwei Ereignisse ![]() und
und ![]() werden als stochastisch unabhängig bezeichnet, wenn sie ihr Eintreten nicht gegenseitig beeinflussen. Dies kann rechnerisch durch die Gleichung:
werden als stochastisch unabhängig bezeichnet, wenn sie ihr Eintreten nicht gegenseitig beeinflussen. Dies kann rechnerisch durch die Gleichung:
![]()
nachgewiesen werden. Zur Überprüfung der Unabhängigkeit setzten wir die Wahrscheinlichkeiten aus der Vierfeldertafel in diese Gleichung ein.
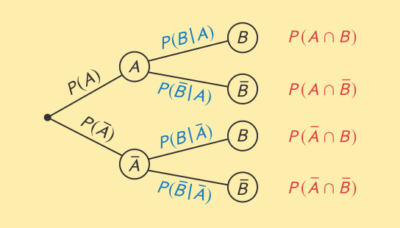
Vierfeldertafel und Baumdiagramm
Die Wahrscheinlichkeiten eines Baumdiagramms mit vier Ästen (zwei Stufen mit je zwei Verzweigungen) können in einer Vierfeldertafel mit relativen Häufigkeiten dargestellt werden und umgekehrt. Dabei entsprechen die Werte der inneren Felder einer Vierfeldertafel den Pfadwahrscheinlichkeiten im Baumdiagramm.
Aufgaben mit Vierfeldertafeln
Bei Aufgaben zur Vierfeldertafel geht es meist um das Aufstellen, Ausfüllen oder Vervollständigen einer Vierfeldertafel. Dazu können wir die Eigenschaft nutzen, dass in den äußeren Feldern die Summe der inneren Felder steht.
Hinweis: Auch wenn in einer Aufgabe das Zeichnen einer Vierfeldertafel nicht explizit verlangt ist, kann diese dir helfen, die Daten zu ordnen und so die Bearbeitung zu erleichtern.
Beispiel:
Von ![]() Puzzleteilen sind
Puzzleteilen sind ![]() dunkel (
dunkel (![]() ) und
) und ![]() Teile bilden den Rand
Teile bilden den Rand ![]() . Von den Randteilen ist die Hälfte dunkel.
. Von den Randteilen ist die Hälfte dunkel.
Wir stellen eine Vierfeldertafel auf, um die Anzahl der hellen Teile zu berechnen, die nicht zum Rand gehören. Dazu tragen wir zunächst die Werte aus der Angabe in die passenden Felder ein. Die Hälfte der Randteile, die dunkel sind, berechnen wir als ![]() .
.

Nun füllen wir die restlichen Felder aus, indem wir Summen und Differenzen bilden.
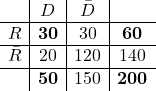
Nun können wir ablesen, dass es ![]() helle (
helle (![]() ) Teile gibt, die nicht zum Rand (
) Teile gibt, die nicht zum Rand (![]() ) gehören.
) gehören.
Häufig gestellte Fragen zum Thema Vierfeldertafel









Alle Artikel aus dem Fach Mathematik