Quotientenregel – Formel, Herleitung und Beispiele

Erfahre, wie die Quotientenregel funktioniert: Ableitung von Funktionen, die als Bruch geschrieben sind. Lerne die Herleitung und Anwendung der Regel, inklusive Beispielen mit -Funktionen und Integration. Dies und vieles mehr findest du im folgenden Text!

Inhaltsverzeichnis zum Thema Quotientenregel

Die Quotientenregel im Überblick

  • Die Quotientenregel ist eine Ableitungsregel für Funktionen, deren Term ein Quotient aus zwei Funktionen ist.
  • Die Quotientenregel lautet:
    f(x) = \dfrac{u(x)}{v(x)} \quad \rightarrow \quad f^\prime(x) = \dfrac{u^\prime(x) \cdot v(x) - u(x) \cdot v^\prime(x)}{\bigl(v(x)\bigr)^2}
  • Neben der Quotientenregel sind die Produktregel und die Kettenregel wichtige Ableitungsregel, die auch zusammen angewendet werden können.
Quotientenregel: Lernvideo

Quelle sofatutor.com

Bildergalerie zum Thema Quotientenregel

Quotientenregel
Quotientenregel
QuotientenregelQuotientenregelQuotientenregel und ProduktregelQuotientenregelQuotientenregelQuotientenregelQuotientenregelQuotientenregel Kürzen

Quotientenregel einfach erklärt

Die Quotientenregel in Mathe ist eine Regel, die es erlaubt, Bruchterme zu differenzieren. Das heißt, wir können mit der Quotientenregel die Ableitung einer Funktion f(x) bestimmen, deren Term ein Bruch aus zwei Funktionen u und v ist, also f(x) = \frac{u(x)}{v(x)}.
Dabei gilt:
f(x) = \dfrac{u(x)}{v(x)} \quad \rightarrow \quad f^\prime(x) = \dfrac{u^\prime(x) \cdot v(x) - u(x) \cdot v^\prime(x)}{\bigl(v(x)\bigr)^2}
Im Zähler der Ableitung f^\prime steht das Produkt aus der Ableitung des Zählers u^\prime(x) mit dem Nenner v(x) des Terms abzüglich des Produkts aus dem Zähler u(x) und der Ableitung des Nenners v^\prime(x). Der Nenner der Ableitung \bigl(v(x)\bigr)^2 entspricht dem Quadrat des Nenners der Funktion f(x).
Quotientenregel Merkregel:
\dfrac{\textbf{ANZ} - \textbf{ZAN}}{\textbf{N}^2}
Dabei steht \textbf{ANZ} für das Produkt aus der Ableitung des Nenners mit dem Zähler, \textbf{ZAN} entsprechend für das Produkt aus dem Zähler und der Ableitung des Nenners und \textbf{N}^2 für das Quadrat des Nenners.

Quotientenregel – Herleitung

Als Beweis für die Quotientenregel wollen wir ihre Gültigkeit aus der Produktregel herleiten. Dazu schreiben wir den Funktionsterm f(x) mithilfe der Potenzgesetze als Produkt:
f(x) = \dfrac{u(x)}{v(x)} = u(x) \cdot \bigl(v(x)\bigr)^{-1}
Für dieses Produkt aus zwei Funktionen kann die Ableitung mit der Produktregel bestimmt werden. Für den zweiten Faktor ergibt sich mit der Kettenregel die Ableitung von \bigl(v(x)\bigr)^{-1} als:
-1 \cdot \bigl(v(x)\bigr)^{-2} \cdot v^\prime(x)
Einsetzen in die Produktregel liefert:
f^\prime(x) = u^\prime(x) \cdot \bigl(v(x)\bigr)^{-1} + u(x) \cdot \Bigl[-v^\prime(x)\bigl(v(x)\bigr)^{-2}\Bigr]
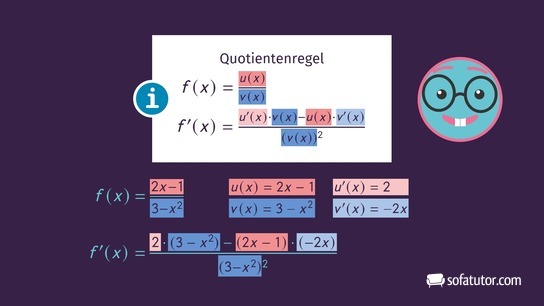
Wir wenden erneut die Potenzgesetze an und erhalten so nach Erweitern auf den gemeinsamen Nenner \bigl(v(x)\bigr)^2 die Quotientenregel:
f^\prime(x) = \dfrac{u^\prime(x)}{v(x)} - \dfrac{u(x) \cdot v^\prime(x)}{\bigl(v(x)\bigr)^{2}} = \dfrac{u^\prime(x) \cdot v(x)}{v(x) \cdot v(x)} - \dfrac{u(x) \cdot v^\prime(x)}{\bigl(v(x)\bigr)^{2}} = \dfrac{u^\prime(x) \cdot v(x) - u(x) \cdot v^\prime(x)}{\bigl(v(x)\bigr)^{2}}

Anleitung zur Anwendung der Quotientenregel

Wir betrachten nun am Beispiel der Funktion f(x) = \frac{2x}{x^2 - 1} Schritt für Schritt, wie du die Quotientenregel anwendest.

  • Wir identifizieren die Funktionen in Zähler und Nenner:
    u(x) = 2x
    v(x) = x^2 - 1
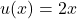
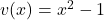
  • Wir bilden die Ableitungen:
    u^\prime(x) = 2
    v^\prime(x) = 2x
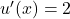
  • Wir setzen in die Quotientenregel ein:
    f^\prime(x) = \dfrac{u^\prime(x) \cdot v(x) - u(x) \cdot v^\prime(x)}{\bigl(v(x)\bigr)^2} = \dfrac{2 \cdot (x^2-1) - 2x \cdot 2x}{\bigl(x^2-1\bigr)^2}
  • Wir fassen zusammen:
    f^\prime(x) = \dfrac{2x^2 - 2 - 4x^2}{\bigl(x^2-1\bigr)^2} = \dfrac{-2x^2 - 2}{\bigl(x^2-1\bigr)^2}

Auf die gleiche Weise lässt sich mit der Quotientenregel die zweite Ableitung f^{\prime\prime} bestimmen:

  • u(x) = -2x^2 - 2
    v(x) = \bigl(x^2-1\bigr)^2
  • u^\prime(x) = -4x
    v^\prime(x) = 2 \cdot (x^2 - 1) \cdot 2x = 4x(x^2 - 1)
  • \begin{array}{rl} f^{\prime\prime}(x) = & \dfrac{-4x \cdot \bigl(x^2-1\bigr)^2 - (-2x^2 - 2) \cdot 4x(x^2 - 1)}{ \bigl(x^2-1\bigr)^4} \ = & \dfrac{-4x\bigl(x^2-1\bigr)^2 + 8x(x^2 + 1)(x^2 - 1)}{ \bigl(x^2-1\bigr)^4} \ = & \dfrac{-4x(x^2-1) \cdot \left[(x^2-1) - 2(x^2 + 1)\right]}{ \bigl(x^2-1\bigr)^4} \ = & \dfrac{-4x \left[x^2 - 1 - 2x^2 - 2\right]}{ \bigl(x^2-1\bigr)^3} \ = & \dfrac{4x^3 + 12x}{ \bigl(x^2-1\bigr)^3} \end{array}

Quotientenregel mit der e-Funktion

Die Quotientenregel kann auch auf Bruchterme angewendet werden, die eine e-Funktion enthalten. Wir betrachten hierzu das Beispiel: f(x) = \dfrac{x^2 + 3}{e^x}

  • u(x) = x^2 + 3
    v(x) = e^x
  • u^\prime(x) = 2x
    v^\prime(x) = e^x
  • f^\prime(x) = \dfrac{2x \cdot e^x - (x^2 + 3) \cdot e^x}{\bigl(e^x\bigr)^2} = \dfrac{e^x(2x - x^2 - 3)}{\bigl(e^x\bigr)^2} = \dfrac{-x^2 + 2x - 3}{e^x}

Hinweis: Steht die e-Funktion e^x wie in diesem Beispiel im Nenner, kann in der Ableitung stets gekürzt werden, da sie sich beim Ableiten nicht verändert und somit im Zähler der Ableitung ausgeklammert werden kann.

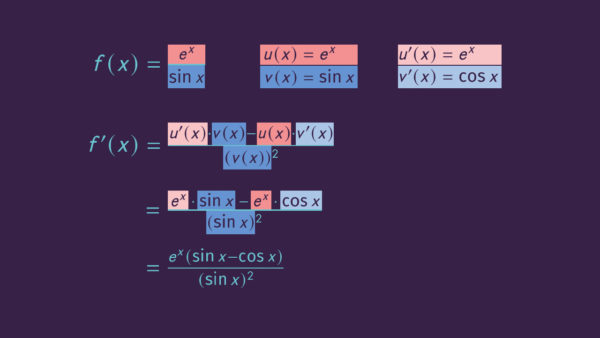
Hier siehst du ein weiteres Beispiel zu einer Quotientenregel mit e-Funktion, bei dem die e-Funktion im Zähler des Bruchs vorkommt:

Quotientenregel e-Funktion Beispiel

Quotientenregel und Integral

Für die Integration gibt es keine Entsprechung der Quotientenregel bei der Ableitung. Beim Integrieren eines Bruchterms kann anstelle einer Quotientenregel die partielle Integration oder Integration durch Substitution genutzt werden.
Andererseits können wir die Korrektheit einer gegebenen Stammfunktion der Form F(x) = \dfrac{u(x)}{v(x)} nachweisen, indem wir mit der Quotientenregel F^\prime(x) = f(x) zeigen.

Häufig gestellte Fragen zum Thema Quotientenregel

Die Quotientenregel kann angewendet werden, wenn die Ableitung einer Funktion der Form f(x) = \frac{u(x)}{v(x)} bestimmt werden soll. Dabei sind u(x) und v(x) Funktionen.

Die Quotientenregel wird benötigt, um die Ableitung von Funktionen zu bilden, deren Funktionsterm ein Quotient aus zwei Funktionen ist. Der Funktionsterm wird dann als Bruch der Form f(x) = \frac{u(x)}{v(x)} geschrieben.

Die Quotientenregel funktioniert für Funktionen f(x) = \frac{u(x)}{v(x)}, indem Zähler u(x) und Nenner v(x) eines Bruchs abgeleitet und in die Formel f^\prime(x) = \frac{u^\prime(x) \cdot v(x) - u(x) \cdot v^\prime(x)}{\bigl(v(x)\bigr)^2} für die Ableitung eingesetzt werden.
Die Quotientenregel lautet:
f(x) = \dfrac{u(x)}{v(x)} \quad \rightarrow \quad f^\prime(x) = \dfrac{u^\prime(x) \cdot v(x) - u(x) \cdot v^\prime(x)}{\bigl(v(x)\bigr)^2}

Die Quotientenregel ist eine Ableitungsregel für Funktionen, deren Funktionsterm ein Bruch aus zwei Funktionen ist.

Die Quotientenregel besagt, dass die Ableitung einer Funktion der Form f(x) = \frac{u(x)}{v(x)} mit der Formel f^\prime(x) = \frac{u^\prime(x) \cdot v(x) - u(x) \cdot v^\prime(x)}{\bigl(v(x)\bigr)^2} gebildet werden kann. Dabei sind u und v Funktionen.

Die Quotientenregel für f(x) = \frac{u(x)}{v(x)} kann hergeleitet werden, indem wir den Quotienten \frac{u(x)}{v(x)} mit den Potenzgesetzen zu einem Produkt umschreiben und die Produktregel anwenden. Es gilt:
f(x) = \dfrac{u(x)}{v(x)} = u(x) \cdot \bigl(v(x)\bigr)^{-1}

Mit der Quotientenregel kann die Ableitung einer Funktion der Form f(x) = \frac{u(x)}{v(x)} berechnet werden. Durch mehrfaches Anwenden ergeben sich auch die höheren Ableitungen.

Mit der Quotientenregel kann eine Funktion der Form f(x) = \frac{u(x)}{v(x)} direkt, das heißt ohne vorherige Umformung, abgeleitet werden. Es ist auch möglich, den Funktionsterm zunächst durch Anwendung der Potenzgesetze als Produkt zu schreiben:
f(x) = \frac{u(x)}{v(x)} = u(x) \cdot \bigl(v(x)\bigr)^{-1}

Dann wird für das weitere Vorgehen zusätzlich zur Produktregel auch die Kettenregel benötigt.

Super! Das Thema: kannst du schon! Teile deine Learnings und Fragen mit der Community!

Alle Artikel aus dem Fach Mathematik