Gewinnfunktion und Erlösfunktion berechnen und maximieren
Verstehe Gewinn- und Erlösfunktionen: Die Erlösfunktion berechnet den Umsatz eines Produkts, während die Gewinnfunktion den tatsächlichen Gewinn angibt. Entdecke, wie man sie berechnet, Gewinn maximiert und den Unterschied zwischen Monopol und Polypol versteht.
Inhaltsverzeichnis zum Thema Gewinnfunktion und Erlösfunktion
Wie willst du heute lernen?
Erlösfunktion – Formel
Die Erlösfunktion ![]() gibt an, wie groß der Umsatz durch den Verkauf eines Produkts ist. Manchmal wird die Erlösfunktion deshalb auch Umsatzfunktion genannt. Sie ist das Produkt aus dem Stückpreis
gibt an, wie groß der Umsatz durch den Verkauf eines Produkts ist. Manchmal wird die Erlösfunktion deshalb auch Umsatzfunktion genannt. Sie ist das Produkt aus dem Stückpreis ![]() und der Anzahl
und der Anzahl ![]() der verkauften Produkte. Die Funktion
der verkauften Produkte. Die Funktion ![]() beschreibt den Stückpreis in Abhängigkeit von der Absatzmenge
beschreibt den Stückpreis in Abhängigkeit von der Absatzmenge ![]() . Der Stückpreis hängt von der Absatzmenge ab, weil Kunden z. B. weniger pro Stück bezahlen müssen, je mehr Stück sie abnehmen. Die Funktion
. Der Stückpreis hängt von der Absatzmenge ab, weil Kunden z. B. weniger pro Stück bezahlen müssen, je mehr Stück sie abnehmen. Die Funktion ![]() wird daher auch Preis-Absatz-Funktion genannt.
wird daher auch Preis-Absatz-Funktion genannt.
![]()
Erlösfunktion – Monopol und Polypol
Wird das Produkt nur von einem Anbieter verkauft, spricht man von einem Monopol. Gibt es mehrere Anbieter, die das gleiche Produkt verkaufen, spricht man von einem Polypol.
Je nachdem ob es sich um ein Monopol oder Polypol handelt, ändert sich die Formel für die Preis-Absatz-Funktion und die Erlösfunktion. Bei einem Monopol verwendet man als Preis-Absatz-Funktion eine lineare Funktion ![]() . Bei einem Polypol-Markt ist der Verkaufspreis für alle Anbieter gleich und unabhängig von der Absatzmenge. Daher ist
. Bei einem Polypol-Markt ist der Verkaufspreis für alle Anbieter gleich und unabhängig von der Absatzmenge. Daher ist ![]() eine Konstante und keine Funktion von
eine Konstante und keine Funktion von ![]() .
.
| Erlösfunktion |
|
|---|---|
| Monopol | Polypol |
Erlösfunktion – Beispiel
Stell dir vor, du möchtest auf eurem Schulfest Waffeln verkaufen. Eine Waffel soll ![]() kosten – unabhängig davon, wie viele Waffeln jemand kauft. Du verwendest also
kosten – unabhängig davon, wie viele Waffeln jemand kauft. Du verwendest also ![]() – unabhängig von
– unabhängig von ![]() . Die Erlösfunktion ist dann
. Die Erlösfunktion ist dann ![]() .
.
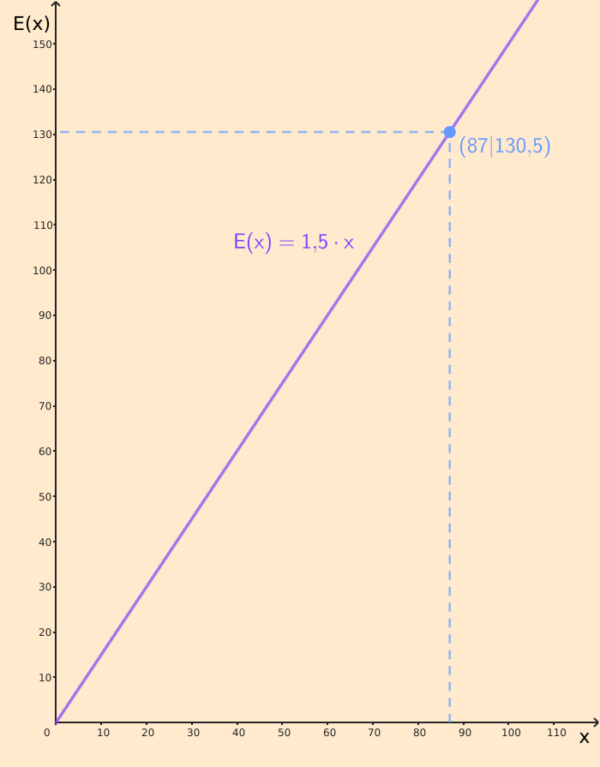
Insgesamt verkaufst du ![]() Waffeln auf dem Schulfest. Wir berechnen den Umsatz mit der Erlösfunktion:
Waffeln auf dem Schulfest. Wir berechnen den Umsatz mit der Erlösfunktion:
![]()
Somit hast du einen Umsatz von ![]() gemacht.
gemacht.
Gewinnfunktion einfach erklärt
Die Gewinnfunktion ![]() ist die Differenz aus der Erlösfunktion und der Kostenfunktion.
ist die Differenz aus der Erlösfunktion und der Kostenfunktion.
![]()
Die Gewinnfunktion beschreibt den Gewinn, den ein Unternehmen mit dem Verkauf eines Produkts in Abhängigkeit von der Absatzmenge ![]() macht.
macht.
Die Kostenfunktion ist die Summe aus den fixen und den variablen Kosten des Produkts bei der Absatzmenge ![]() :
:
![]()
Für die Gewinnfunktion ergibt sich damit:
![]()
Die Gewinnfunktion gibt also an, ob und wie viel Gewinn oder Verlust mit dem Verkauf eines Produkts erzielt wird.
Ist ![]() , wird ein Gewinn erzielt.
, wird ein Gewinn erzielt.
Ist ![]() , handelt es sich um einen Verlust.
, handelt es sich um einen Verlust.
Bei ![]() ist der sogenannte Break-even-Point erreicht (
ist der sogenannte Break-even-Point erreicht (![]() ).
).
Gewinnfunktion ableiten – Steigung
Die Steigung der Gewinnfunktion wird beschrieben durch ihre Ableitung ![]() . Bei einem Monopol-Markt kannst du das Maximum der Gewinnfunktion in Abhängigkeit von der Absatzmenge
. Bei einem Monopol-Markt kannst du das Maximum der Gewinnfunktion in Abhängigkeit von der Absatzmenge ![]() suchen. Falls die Gewinnfunktion ein relatives Maximum besitzt, liegt dieses an der Nullstelle der Ableitungsfunktion. An dieser Stelle
suchen. Falls die Gewinnfunktion ein relatives Maximum besitzt, liegt dieses an der Nullstelle der Ableitungsfunktion. An dieser Stelle ![]() ist der Gewinn, also die Differenz aus Erlös und Kosten, maximal im Vergleich zu anderen Stellen
ist der Gewinn, also die Differenz aus Erlös und Kosten, maximal im Vergleich zu anderen Stellen ![]() in der Nähe.
in der Nähe.
Um herauszufinden, wie groß der größtmögliche Gewinn ist und für welches ![]() dieser existiert, kannst du dich an den folgenden Schritten orientieren:
dieser existiert, kannst du dich an den folgenden Schritten orientieren:
Leite die Funktion ![]() ab.
ab.
Setze die Ableitung ![]() gleich null und löse nach der Variablen auf.
gleich null und löse nach der Variablen auf.
Setze das Ergebnis in die Funktion ![]() ein, um den maximalen Gewinn zu berechnen.
ein, um den maximalen Gewinn zu berechnen.
Dabei ist ![]() die Absatzmenge, für die der Gewinn maximal wird.
die Absatzmenge, für die der Gewinn maximal wird.
Gewinnfunktion – Beispiel
In dem Beispiel oben zur Erlösfunktion verkaufst du Waffeln auf dem Schulfest zum Stückpreis von ![]() und erzielst beim Verkauf von
und erzielst beim Verkauf von ![]() Waffeln einen Umsatz von
Waffeln einen Umsatz von ![]() . Für den Teig hast du insgesamt
. Für den Teig hast du insgesamt ![]() bezahlt. Es ist also
bezahlt. Es ist also ![]() . Zusätzlich zu einer Waffel gibst du Pappteller für umgerechnet
. Zusätzlich zu einer Waffel gibst du Pappteller für umgerechnet ![]() pro Stück raus. Somit ist
pro Stück raus. Somit ist ![]() .
.
Aus den Fixkosten und den variablen Kosten erhältst du die Kostenfunktion:
![]()
Aus der Kostenfunktion und der Erlösfunktion erhältst du die Gewinnfunktion:
![]()
Setze die Absatzmenge ![]() entweder in die Formel für die Gewinnfunktion direkt oder in die Erlösfunktion und in die Kostenfunktion einzeln ein und du erhältst:
entweder in die Formel für die Gewinnfunktion direkt oder in die Erlösfunktion und in die Kostenfunktion einzeln ein und du erhältst:
![]()
Dir bleibt also ein Gewinn von ![]() .
.
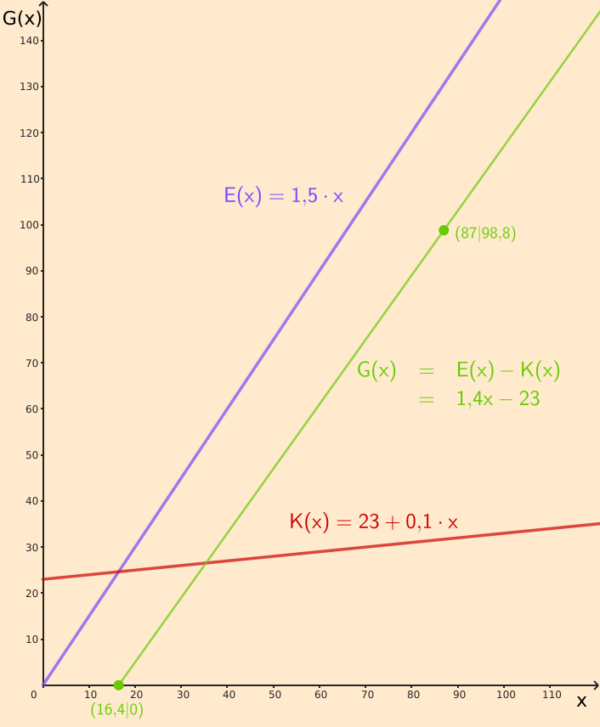
Da du keinen Preisnachlass gibst, wenn jemand mehrere Waffeln kauft, ist der Preis der Waffeln unabhängig von der Absatzmenge ![]() . Du brauchst kein lokales Maximum der Gewinnfunktion zu suchen, denn der Gewinn steigt linear mit der Absatzmenge. Je mehr Waffeln du verkaufst, desto größer ist der Gewinn.
. Du brauchst kein lokales Maximum der Gewinnfunktion zu suchen, denn der Gewinn steigt linear mit der Absatzmenge. Je mehr Waffeln du verkaufst, desto größer ist der Gewinn.
An der Nullstelle der Gewinnfunktion erkennst du zudem, dass du ab ![]() verkauften Waffeln Gewinn machst. Du musst also mindestens
verkauften Waffeln Gewinn machst. Du musst also mindestens ![]() Waffeln verkaufen, um keinen Verlust zu machen.
Waffeln verkaufen, um keinen Verlust zu machen.
Häufig gestellte Fragen zum Thema Gewinnfunktion und Erlösfunktion









Alle Artikel aus dem Fach Mathematik