Drachenviereck Flächeninhalt – Definition, Eigenschaften und Formeln
Ein Drachenviereck ist ein symmetrisches Viereck mit besonderen Eigenschaften. Seine Fläche wird durch die Diagonalen definiert. Lerne, wie man den Flächeninhalt berechnet und mehr über die Eigenschaften des Drachenvierecks. Dies und vieles mehr findest du im folgenden Text.
Inhaltsverzeichnis zum Thema Drachenviereck Flächeninhalt
Das Quiz zum Thema: Drachenviereck Flächeninhalt
Was ist eine grundlegende Eigenschaft eines Drachenvierecks?
Frage 1 von 4
Welche Aussage über die Diagonalen eines Drachenvierecks ist richtig?
Frage 2 von 4
Was besagt die Symmetrieeigenschaft eines Drachenvierecks?
Frage 3 von 4
Welche der folgenden Figuren ist immer auch ein Drachenviereck?
Frage 4 von 4
Wie willst du heute lernen?
Bildergalerie zum Thema Drachenviereck Flächeninhalt
Eigenschaften eines Drachenvierecks
Ein Drachenviereck ist ein Begriff der Geometrie, der ein Viereck mit besonderen Eigenschaften beschreibt. Die Besonderheiten eines Drachenvierecks sind:
- Je zwei nebeneinander liegende Seiten eines Drachenvierecks sind gleich lang.
- Jedes Drachenviereck hat eine Symmetrieachse.
- Die Diagonalen eines Drachenvierecks schneiden sich im rechten Winkel.
- Ein Drachenviereck hat zwei gleich große gegenüberliegende Winkel.
Wir können ein Drachenviereck im Alltag beispielsweise, wie der Name schon sagt, bei einem Flug- und Winddrachen finden.
Zeichnen eines Drachenvierecks
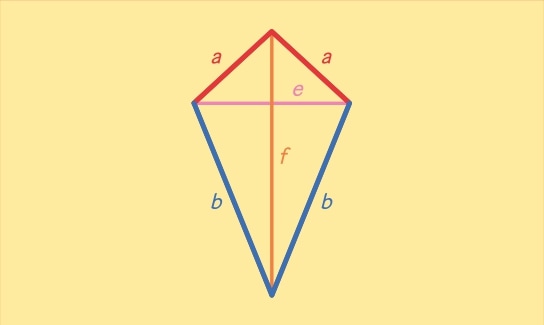
Um ein Drachenviereck zu konstruieren, ist es am einfachsten, mit den Diagonalen zu beginnen. Wir zeichnen die erste Diagonale und konstruieren die zweite Diagonale als Mittelsenkrechte dazu. Das bedeutet, sie steht senkrecht dazu und halbiert die erste Diagonale. Dann können wir die Endpunkte der Diagonalen verbinden und erhalten ein Drachenviereck. Zuletzt ergänzen wir die Beschriftung des Drachenvierecks.
Berechnungen zum Drachenviereck
Je nachdem, welche Größen wir gegeben haben, können wir beim Drachenviereck berechnen, wie groß sein Flächeninhalt oder sein Umfang ist. Auch fehlende Winkel können wir ermitteln.
Flächeninhalt eines Drachenvierecks
Die Fläche eines Drachenvierecks setzt sich aus zwei kongruenten Dreiecken zusammen, welche durch die Diagonale ![]() voneinander getrennt werden. Für die Herleitung des Flächeninhalts des Drachenvierecks können wir also den Flächeninhalt eines dieser Dreiecke berechnen und verdoppeln. Für den Flächeninhalt eines Dreiecks gilt:
voneinander getrennt werden. Für die Herleitung des Flächeninhalts des Drachenvierecks können wir also den Flächeninhalt eines dieser Dreiecke berechnen und verdoppeln. Für den Flächeninhalt eines Dreiecks gilt:
![]()
Dabei stehen die Grundseite ![]() und die Höhe
und die Höhe ![]() senkrecht aufeinander. Bei uns bildet die Diagonale
senkrecht aufeinander. Bei uns bildet die Diagonale ![]() die Grundseite der Dreiecke und die halbe Diagonale
die Grundseite der Dreiecke und die halbe Diagonale ![]() , also
, also ![]() , die Höhe der Dreiecke. Der Flächeninhalt eines Dreiecks ist damit:
, die Höhe der Dreiecke. Der Flächeninhalt eines Dreiecks ist damit:
![]()
Um im Drachenviereck den Flächeninhalt zu berechnen, verdoppeln wir den Flächeninhalt und erhalten:
![]()
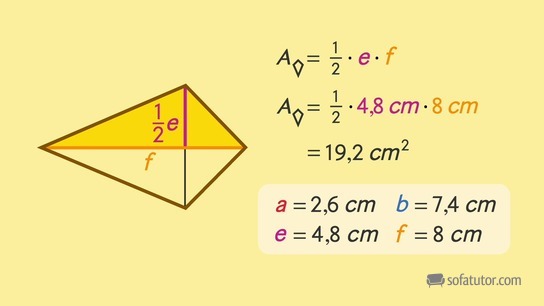
Beispiel: Ein Drachenviereck hat die Diagonalen ![]() und
und ![]() . Der Flächeninhalt lässt sich wie folgt berechnen:
. Der Flächeninhalt lässt sich wie folgt berechnen:
![]()
Wir können die Formel für den Flächeninhalt des Drachenvierecks auch umstellen, um die Länge einer der Diagonalen zu berechnen:
Beispiel: ![]() und
und ![]() sind gegeben, wir suchen
sind gegeben, wir suchen ![]() .
.
Wir stellen um:
![]()
und setzen ein:
![]()
Hinweis: Achte auf korrekte Bezeichnungen: Ein Volumen können wir beim Drachenviereck nicht berechnen. Dies ist ein Begriff, der sich auf einen dreidimensionalen Körper bezieht. Beim Drachenviereck handelt es sich hingegen um eine zweidimensionale Fläche.
Das Drachenviereck kann jedoch eine Außenfläche eines Körpers sein. Ist beispielsweise die Grundfläche eines Prismas ein Drachenviereck, können wir berechnen, was das Volumen und der Oberflächeninhalt des Prismas sind.
Umfang des Drachenvierecks
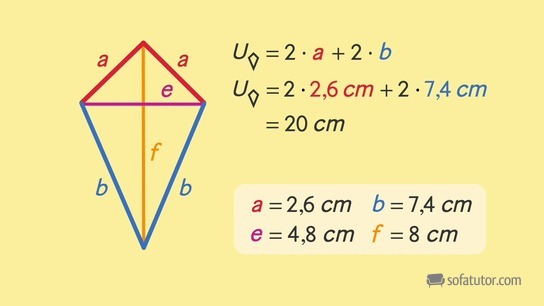
Um den Umfang einer ebenen Figur zu berechnen, addieren wir alle Seitenlängen. Da in einem Drachenviereck jeweils benachbarte Seiten gleich lang sind, können wir die Formel zusammenfassen:
![]()
Winkel im Drachenviereck
Jedes Drachenviereck ist ein symmetrisches Drachenviereck. Daher sind zwei der Innenwinkel gleich groß.
Seien beispielsweise die beiden Winkel ![]() und
und ![]() gegeben und die beiden gleich großen Winkel
gegeben und die beiden gleich großen Winkel ![]() und
und ![]() gesucht. Wir können die fehlenden Winkel im Drachenviereck über die Winkelsumme im Viereck berechnen:
gesucht. Wir können die fehlenden Winkel im Drachenviereck über die Winkelsumme im Viereck berechnen:
![]()
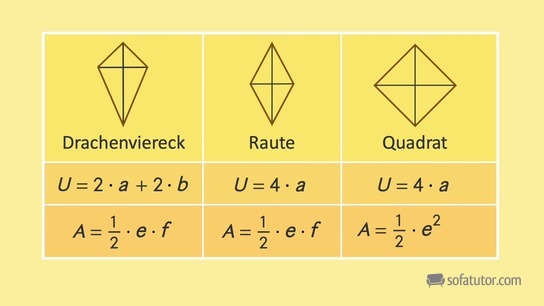
Vergleich des Drachenvierecks mit anderen Vierecken
Das Haus der Vierecke hilft uns, die Eigenschaften von Drachenvierecken mit anderen Vierecken zu vergleichen.
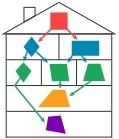
Das Drachenviereck liegt in der mittleren Ebene ganz links.
Im Haus der Vierecke liegt ein Viereck umso höher, je mehr Eigenschaften es hat. Ein Viereck hat daher immer auch die Eigenschaften der Vierecke unter ihm, mit denen es durch einen Pfeil verbunden ist.
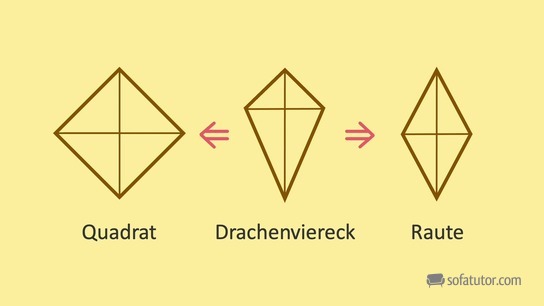
Wir können also beispielsweise formulieren:
Jede Raute ist auch ein Drachenviereck, da eine Raute alle Eigenschaften eines Drachenvierecks hat.
Die Aussage „jedes Trapez ist ein Drachenviereck” ist hingegen falsch, da das Trapez im Haus der Vierecke unterhalb des Drachenvierecks liegt.
Häufig gestellte Fragen zum Thema Drachenviereck













Alle Artikel aus dem Fach Mathematik