Zahlen lernen für Grundschulkinder
Zahlen bestehen aus Ziffern, aber was genau ist der Unterschied? Ziffern sind die Bausteine von Zahlen, von 0 bis 9. Erfahre, wie du Zahlen im Zehnersystem darstellst und ihren Wert ablesen kannst.
Inhaltsverzeichnis zum Thema Zahlen
Zahlen im Überblick
Quelle sofatutor.com
Wie willst du heute lernen?
Zahlen und Ziffern
Hast du dich schon einmal gefragt, was der Unterschied zwischen Ziffern und Zahlen ist?
Ziffern und Zahlen haben unterschiedliche Bedeutungen. Ziffern sind Bestandteile von Zahlen. Zahlen bestehen also immer aus einzelnen Ziffern. Es gibt diese Ziffern:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Aus diesen Ziffern kannst du alle Zahlen bilden, egal wie groß die Zahl ist.
Zahlen darstellen
Unsere Zahlen werden im Zehnersystem dargestellt, das bedeutet, dass immer Vielfache von 10 in die nächstgrößere Einheit gebündelt werden.
Das kannst du gut mit Eiern und Eierkartons verstehen:
Links im Bild siehst du insgesamt 14 Eier. Immer 10 werden in einen Eierkarton gelegt.
Du hast nun also einen vollen Karton mit zehn Eiern (1 Zehner) und vier einzelne Eier (4 Einer).
Das kannst du auch in einer Stellenwerttafel notieren:
| Z | E |
|---|---|
| 1 | 4 |
Dabei steht E für Einer und Z für Zehner.
Merke: Du beginnst beim Eintragen von Ziffern in die Stellenwerttafel immer ganz rechts bei der Einerstelle und gehst dann immer eine Stelle nach links weiter.
Um die Anzahl an Eiern nun als Zahl aufzuschreiben, musst du wissen, dass dir die Stelle der Ziffer in der Zahl Auskunft über deren Wert gibt. Die Ziffer ganz rechts in einer Zahl steht immer für die Einer, die Ziffer links daneben steht für die Zehner.
Die Zahl 14 steht also für 1 
10 + 4 1.
Wie viele Eier sind hier dargestellt?
Es sind zwei volle Eierkartons mit zehn Eiern (2 Zehner) und 8 einzelne Eier (8 Einer).
In die Stellenwerttafel eingetragen sieht das so aus:
| Z | E |
|---|---|
| 2 | 8 |
Und als Zahl wird es so geschrieben: 28
Dabei wird sie so gebildet: 28 = 2 10 + 8 1.
Auch bei größeren Zahlen hängt der Wert einer Ziffer von der Stelle in der Zahl ab. Die nächste Stelle nach den Zehnern ist die Hunderterstelle, denn zehn Zehner werden zu einem Hunderter gebündelt.
Im folgenden Bild wird eine Zahl dargestellt. Aus wie vielen Einern, Zehnern und Hundertern besteht die Zahl?
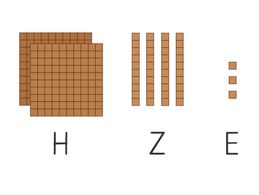
Die Zahl besteht aus 3 Einern, 4 Zehnern und 2 Hundertern.
In die Stellenwerttafel wird das so eingetragen:
| H | Z | E |
|---|---|---|
| 2 | 4 | 3 |
Die Zahl lautet also 243. Dabei wird sie so gebildet: 243 = 2 100 + 4 10 + 3 1.
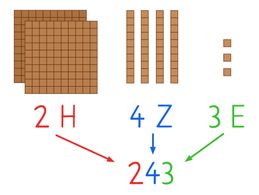
Weißt du auch, welche Zahl hier dargestellt wird?
2 H, 3 Z, 4 E
Tipp: E steht für Einer, Z steht für Zehner, H steht für Hunderter. In die Stellenwerttafel eingetragen sieht das so aus:
| H | Z | E |
|---|---|---|
| 2 | 3 | 4 |
Die Zahl lautet also 234. Sie wird so gebildet: 234 = 2 100 + 3 10 + 4 1.
Probiere in den Übungen aus, die passende Zahl zu finden.
Übung 1: Welche Zahl wird hier dargestellt?
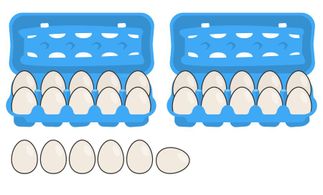
Übung 2: Welche Zahl wird hier dargestellt?
Übung 3: Welche Zahl wird hier dargestellt?
1 Z, 2 E
Übung 4: Welche Zahl wird hier dargestellt?
4 H, 3 E, 2 Z
Lösungen:
Übung 1: 26
Übung 2: 251
Übung 3: 12
Übung 4: 423
Hinweis: Wir arbeiten meistens im Zehnersystem, denn unsere Zahlen werden darin dargestellt. Es gibt auch andere Zahlensysteme.
Bei unserer Zeitrechnung verwenden wir zum Beispiel nicht das Zehnersystem, sondern das Sechzigersystem, das heißt, immer 60 werden zur nächstgrößeren Einheit gebündelt: 60 Sekunden entsprechen 1 Minute und 60 Minuten entsprechen 1 Stunde. Binärzahlen sind Zahlen, die im Zweiersystem dargestellt werden, diese werden oft bei Computern verwendet.
Zahlen schreiben
Ziffern und Zahlen werden nach bestimmten Regeln geschrieben. Diese Regeln erfährst du in den nächsten Abschnitten.
Ziffern schreiben
Weil du aus den Ziffern 0 bis 9 alle Zahlen bilden kannst, musst du dir nur die Schreibweise dieser Zahlen merken. Im Bild siehst du, wie die Zahl 2 geschrieben wird:
Zahlwörter und Zahlen
Manchmal hörst du nur ein Zahlwort und sollst dazu die passende Zahl aufschreiben. Dabei musst du dir merken, dass wir zuerst die Einerstelle nennen und danach die Zehnerstelle.
Die Zahl zum Zahlwort vierzehn lautet also 14.
Ausnahmen bilden nur die Zahlwörter der 11 und der 12, denn diese haben besondere Zahlwörter:
| Zahl | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| Zahl-wort | elf | zwölf | dreizehn | vierzehn | fünfzehn | sechzehn | siebzehn | achtzehn | neunzehn | zwanzig |
Rechnen mit Zahlen
Du weißt nun, dass unsere Zahlen im Zehnersystem dargestellt werden und immer Vielfache von 10 gebündelt werden. Das hilft dir, mit Zahlen zu rechnen.
Addition
Bei Plusaufgaben fasst du zwei Teilmengen zusammen oder fügst einer Teilmenge eine weitere Teilmenge hinzu.
Hier ist die Aufgabe 9 + 9 mit blauen und roten Plättchen dargestellt:
Wie du siehst, entspricht die Gesamtmenge der Plättchen einem ganzen Zehner (1 Z) und acht Einern (8 E).
Also ist 9 + 9 = 18.
Subtraktion
Bei Minusaufgaben ziehst du eine Teilmenge von der Gesamtmenge ab oder ergänzt von der Teilmenge zur Gesamtmenge.
Hier ist die Aufgabe 20 – 9 mit Plättchen dargestellt, die teilweise durchgestrichen sind:
Wie du siehst, werden neun Plättchen (9 Einer) von den zwanzig Plättchen (2 Zehner) abgezogen. Um die 9 Plättchen abzuziehen, wird ein Zehner in zehn Einer entbündelt. Davon kannst du nun neun Einer abziehen. Übrig bleiben ein Zehner (1 Z) und ein Einer (1 E). Das sind noch 11 Plättchen.
Also ist 20 – 9 = 11.
Zahlenrätsel
Jetzt kennst du dich schon ziemlich gut mit Zahlen aus. Bestimmt kannst du dann auch folgendes Zahlenrätsel lösen:
Welche Zahl erhältst du, wenn du zur Zahl 7 noch 3 addierst und vom Ergebnis 5 subtrahierst?
Genau, es ist die Zahl 5, denn 7 + 3 = 10 und 10 – 5 = 5.
Probiere noch ein Zahlenrätsel aus:
Du beginnst mit der Zahl 100. Davon subtrahierst du 90 und zum Ergebnis addierst du die 3.
Du erhältst die Zahl 13, denn 100 – 90 = 10 und 10 + 3 = 13.
Zahlenarten
In der Grundschule sind vor allem die natürlichen Zahlen wichtig. Das sind die Zahlen, die du auch zum Zählen verwendest:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …
Es gibt aber auch andere Zahlenarten, zum Beispiel die rationalen Zahlen, sie werden auch Bruchzahlen genannt. Stell dir vor, du hast eine Pizza vor dir liegen. Nun isst du davon die Hälfte. Jetzt ist noch 
Pizza (eine halbe Pizza) übrig. Du hast die Menge an Pizza als Bruchzahl angegeben. Den Bruch kannst du auch als Dezimalzahl (Kommazahl) angeben, denn = 0,5.
Hier siehst du noch ein paar andere Bruchzahlen mit Pizzastücken dargestellt:
Später in der weiterführenden Schule kommen noch weitere Zahlenarten hinzu, zum Beispiel die negativen Zahlen. Das sind alle Zahlen mit einem Minus als Vorzeichen. Auf dem Zahlenstrahl werden sie links von der Null dargestellt:
Alle natürlichen Zahlen und negativen Zahlen gemeinsam ergeben die ganzen Zahlen.
Auch von irrationalen Zahlen und Primzahlen erfährst du in der weiterführenden Schule.
Fibonacci-Zahlen
Hast du schon einmal etwas von den Fibonacci-Zahlen gehört?
Die Fibonacci-Zahlen sind eine Folge von ganzen positiven Zahlen. Um die nächste Fibonacci-Zahl zu erhalten, musst du die beiden vorhergegangenen Zahlen addieren. Die ersten beiden Zahlen kannst du aber nicht mithilfe dieser Regel bilden:
| Fibonacci-Zahl | 1 | 1 | 2 | 3 | 5 | 8 | 13 |
|---|---|---|---|---|---|---|---|
| Bildungsregel | 1 + 1 | 1 + 2 | 2 + 3 | 3 + 5 | 5 + 8 |
Die Fibonacci-Zahlen können auch geometrisch dargestellt werden, dann erhältst du ein Schneckenhaus:
Sie wird auch goldene Spirale genannt und wird für die Gestaltung von Bildern verwendet, damit die Positionierung schöner aussieht.
Neben der goldenen Spirale gibt es auch den Goldenen Schnitt, der ebenfalls für die Kunst eingesetzt wird. Beim Goldenen Schnitt wird ein ganz bestimmtes Zahlenverhältnis genutzt:
(a + b) : a = a : b
Dadurch sollen Bilder harmonischer wirken.
Häufig gestellte Fragen zum Thema Zahlen
Eine Zahl ist ein Zeichen, das eine Menge von Gegenständen beschreibt. Die Zahl 8 beschreibt beispielsweise eine Menge von acht Gegenständen, das können acht Äpfel, acht Bauklötze oder acht Kinder sein.
Zahlen setzen sich aus Ziffern zusammen, die Zahl 12 besteht dabei aus den Ziffern 1 und 2. Die Stelle der Ziffern in der Zahl sagt etwas über ihren Wert aus. Die Ziffer 2 in der Zahl 12 zeigt dir, dass die Zahl zwei Einer enthält. Die Ziffer 1 in der Zahl 12 zeigt dir, dass die Zahl einen Zehner enthält.
Beim Zählen gibt es eine festgelegte Reihenfolge an Zahlen, die du durchläufst. Dabei ist wichtig, dass du jeden Gegenstand, den du zählen möchtest, genau einmal zählst.
So kannst du auch Zahlen zählen. Dabei musst du abzählen, wie viele Zahlen es insgesamt sind.
Zähle ab, wie viele Zahlen hier stehen:
1, 3, 5, 7, 9
Insgesamt stehen hier 5 Zahlen.
Es gibt unendlich viele Zahlen, denn aus den Ziffern 0 bis 9 kannst du beliebig große Zahlen bilden.
Ziffern sind Bestandteile von Zahlen. Zahlen bestehen also immer aus einzelnen Ziffern.
Von den Ziffern gibt es insgesamt nur zehn Stück: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Zahlen gibt es unendlich viele, weil du mit diesen zehn Ziffern beliebig große Zahlen bilden kannst.
Für die Ziffern 0 bis 9 gibt es bestimmte Schreibregeln, die du kennen solltest. Dann kannst du auch größere Zahlen schreiben, weil diese immer nur aus den zehn Ziffern zusammengesetzt sind.
Bei Zahlen aus mehr als einer Ziffer musst du wissen, dass jede Stelle der Zahl etwas über ihren Wert aussagt. So stehen bei einer Zahl an der Stelle ganz rechts die Einer, eine Stelle weiter links stehen die Zehner und so weiter.
Zahlen ordnest du normalerweise nach ihrer Größe. Jede Zahl steht für eine bestimmte Anzahl bzw. Menge. So steht die Zahl 1 für eine Menge mit einem Gegenstand. Die Zahl 3 steht für eine Menge mit drei Gegenständen. Deshalb ist die Zahl 3 größer als die Zahl 1.
Das kannst du auch mit dem „kleiner als“-Zeichen darstellen:
1 < 3
Das bedeutet: 1 ist kleiner als 3.
Eine Zahlenserie oder Zahlenreihe ist eine Reihe von Zahlen, die durch eine bestimmte Regel gebildet wird.
Schau dir die folgende Zahlenreihe an:
1, 3, 5, 7, 9 …
Wie wird diese Zahlenreihe gebildet?
Um von einer Zahl der Zahlenreihe zur nächsten zu gelangen, wird immer 2 addiert (hinzugefügt). Die Regel lautet also „+ 2“.
Bei einer Zahlentafel bzw. Hundertertafel werden die Zahlen von 1 bis 100 zeilenweise angeordnet. Im folgenden Bild siehst du eine Zahlentafel:
Bewegst du dich um eins nach rechts auf der Zahlentafel, wird jeweils 1 hinzugefügt.
Bewegst du dich um eins nach unten, wird jeweils 10 hinzugefügt.
Zahlendarstellungen sind verschiedene Möglichkeiten, eine Zahl darzustellen.
Du kannst eine Zahl zum Beispiel als Menge von Gegenständen darstellen. Im Bild wird die Zahl 13 als Menge an Äpfeln dargestellt:
Du kannst die Zahl 13 aber auch mit den entsprechenden Zahlzeichen darstellen: 13.
Oder du stellst die Zahl mit dem Zahlwort dar: dreizehn.
Eine Zahl kann verschieden viele Ziffern haben, das hängt von ihrer Größe ab. Es gibt Zahlen mit nur einer Ziffer, zum Beispiel die Zahl 9. Es gibt aber auch Zahlen mit zwei Ziffern (z. B. 98), drei Ziffern (z. B. 238) und so weiter.
Wie viele Ziffern hat die folgende Zahl?
135 264 678
Die Zahl besteht aus 9 Ziffern.
Es gibt verschiedene Zahlenbereiche: Die natürlichen Zahlen (mit und ohne 0), die ganzen Zahlen, die rationalen Zahlen und die irrationalen Zahlen.
Im Bild siehst du eine Darstellung der verschiedenen Zahlenbereiche und wie sie miteinander zusammenhängen. In den rationalen Zahlen sind beispielsweise die natürlichen und die ganzen Zahlen eingeschlossen:
Die rationalen und irrationalen Zahlen zusammen ergeben den Zahlenraum der reellen Zahlen. Die komplexen Zahlen sind wiederum eine Erweiterung der reellen Zahlen.
Natürliche Zahlen sind die Zahlen, die du auch zum Zählen verwendest:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …
Deshalb werden sie auch Zählzahlen genannt.
Rationale Zahlen sind alle Zahlen, die sich als Bruch darstellen lassen, z. B. 
oder . Auch natürliche Zahlen sind dort eingeschlossen, weil sich diese auch als Bruch darstellen lassen, z. B. kannst du die Zahl 1 als 
darstellen.
Eine Dezimalzahl ist eine Kommazahl. Sie besteht aus Vorkommastellen, dem Komma und den Nachkommastellen. Die Zahl 1,5 ist eine Dezimalzahl. Die 1 ist die Vorkommastelle, sie steht für 1 Einer. Die 5 ist die Nachkommastelle, sie steht für 5 Zehntel.
Alle Artikel aus dem Fach Mathematik