Interferenz – Definition, Formel und Bedeutung

Als Interferenz wird die Überlagerung von zwei oder mehreren Wellen bezeichnet. Sie tritt bei allen Arten von Wellen auf. Bei der Interferenz zweier Wellen addieren sich an jedem Ort die Amplituden der beiden Wellen von diesem Ort. Achtung! In Abhängigkeit von den relativen Vorzeichen tritt entweder konstruktive oder destruktive Interferenz auf.

Haben zwei Wellen ihre Maxima und Minima genau an denselben Positionen, sagt man, sie sind in Phase zueinander. Ist dies der Fall, tritt bei der Überlagerung eine konstruktive Interferenz auf. Das bedeutet, dass sich die Wellenberge der ersten Welle mit den Wellenbergen der zweiten Welle addieren und dass sich Wellentäler der ersten Welle mit den Wellentälern der zweiten Welle addieren. Dies führt dazu, dass die Amplitude der resultierenden Welle der Summe der Amplituden der einzelnen Wellen entspricht.

Sind zwei Wellen genau um eine halbe Wellenlänge zueinander verschoben, spricht man von destruktiver Interferenz. Dies hat damit zu tun, dass sich in diesem Fall die Wellenberge der ersten Welle mit den Wellentälern der zweiten Welle addieren und die Wellentäler der ersten Welle mit den Wellentälern der zweiten Welle. Falls beide Wellen die gleiche Amplitude und Wellenlänge haben, führt dies dazu, dass sich beide Wellen gegenseitig vollständig auslöschen. Die resultierende Welle hat dann die Amplitude null. Sind beide Wellen nicht exakt um die halbe Wellenlänge zueinander verschoben oder ist die Amplitude von einer der beiden Wellen größer, tritt eine Überlagerung von konstruktiver und destruktiver Interferenz auf und man erhält eine resultierende Welle mit einer Amplitude zwischen null und der Summe beider Amplituden. Ein solcher Fall ist in der folgenden Abbildung dargestellt.

Sicherlich hast du schon einmal gehört, dass die Beugung und die Interferenz am Doppelspalt die Wellennatur des Lichts nachweisen. Damit du auch weißt, warum das so ist, wollen wir uns im Folgenden die Interferenz am Doppelspalt genauer anschauen.

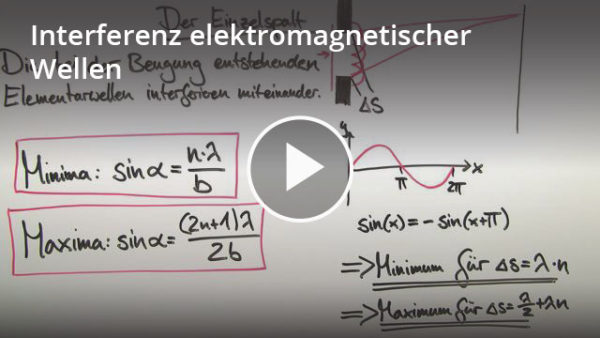
Trifft monochromatisches Licht, also Licht, das nur aus einer Wellenlänge besteht, auf einen Doppelspalt, kann in einem gewissen Abstand hinter dem Spalt ein Interferenzmuster betrachtet werden. Dieses Interferenzmuster ist der Nachweis für die Wellennatur des Lichts, da ohne die Welleneigenschaften auf dem Schirm hinter dem Spalt einfach nur zwei Lichtstreifen zu sehen wären. Doch wie entstehen diese? Die Spalten sind so schmal gewählt, dass nach dem huygensschen Prinzip der Elementarwellen nur eine Welle durch jeden Spalt gelangen kann, die anschließend wieder zum Ausgangspunkt einer neuen Welle wird. Da es sich bei unserem Aufbau um einen langen Spalt handelt, vernachlässigen wir die Geometrie des Spalts in der z-Achse und betrachten die durch die Spalte laufenden Wellen als Zylinderwellen. Da sich die Zylinderwellen mit der Zeit ausbreiten, gibt es einen Punkt, ab dem sich die Wellen aus beiden Spalten gegenseitig überlagern. Um das Interferenzmuster sichtbar machen zu können, ist es notwendig, einen Schirm hinter dem Doppelspalt aufzustellen. Auf dem Schirm können wir nun Intensitätsmaxima und Intensitätsminima sehen. Diese ergeben sich dadurch, dass je nach Position auf dem Schirm beide Wellen einen gewissen Gangunterschied haben, der zu einer relativen Phasendifferenz in Abhängigkeit von der Position führt. Die Phase jeder Welle an der Position auf dem Schirm ergibt sich demnach durch die Wegstrecke geteilt durch die Wellenlänge multipliziert mit .

Somit ergibt sich die Phasendifferenz zu:

Entspricht die Phasendifferenz genau null oder einem Vielfachen von , ergibt sich ein Intensitätsmaximum. Ist die Phasendifferenz genau oder plus ein Vielfaches von , ergibt sich ein Intensitätsminimum.

Maximum bei:
Minimum bei:

Die Position der Maxima und Minima auf dem Schirm lässt sich dann wie folgt berechnen:

Position Maxima:
Position Minima:

Dabei ist der Abstand zwischen den Spalten und die Entfernung des Schirms zum Doppelspalt.

Bei der Interferenz am Gitter sieht es sehr ähnlich aus. Ein Beugungsgitter oder auch optisches Gitter ist nämlich im Prinzip nichts anderes als ein Vielfachspalt oder eine andere sich wiederholende geometrische Struktur zur Beugung von Licht. Für die Intensitätsmaxima und Intensitätsminima gelten daher die gleichen Bedingungen für die Phase. Die Schwierigkeit hierbei ist nur, dass diese Bedingung nun für alle Spalten des Gitters erfüllt sein muss. Der Abstand der Spalte im Gitter wird per Konvention als Gitterkonstante bezeichnet. Bei einem Gitter ergeben sich die Maxima demnach wie folgt:

Maxima: