Ortsfaktor, Fallbeschleunigung und Erdbeschleunigung einfach erklärt
Ortsfaktor und Fallbeschleunigung: Erkläre den Zusammenhang zwischen Ortsfaktor und Fallbeschleunigung. Entdecke, warum sie dasselbe messen, aber unterschiedliche Einheiten haben. Erfahre, wie du die Fallbeschleunigung berechnen kannst und warum sie auf verschiedenen Himmelskörpern variiert.
Inhaltsverzeichnis zum Thema Ortsfaktor und Fallbeschleunigung
Fallbeschleunigung und Ortsfaktor – Definition
Die Fallbeschleunigung bezeichnet die Beschleunigung, die unter Vernachlässigung des Luftwiderstands auf einen frei fallenden Körper wirkt. Das Formelzeichen der Fallbeschleunigung ist ![]() und die Einheit Meter pro Sekunde ins Quadrat
und die Einheit Meter pro Sekunde ins Quadrat ![]() . Die Fallbeschleunigung gibt also an, wie schnell sich die Geschwindigkeit eines Körpers beim freien Fall ändert. Auf der Erdoberfläche beträgt ihr mittlerer Wert:
. Die Fallbeschleunigung gibt also an, wie schnell sich die Geschwindigkeit eines Körpers beim freien Fall ändert. Auf der Erdoberfläche beträgt ihr mittlerer Wert:
![]()
Es wird jedoch auch häufig der Rundungswert von ![]() verwendet.
verwendet.
Die Fallbeschleunigung unterscheidet sich jedoch, je nachdem wo man sich auf der Erde befindet. Am Äquator ist sie mit ![]() am kleinsten und an den Polen mit
am kleinsten und an den Polen mit ![]() am größten. Die Fallbeschleunigung ist also ortsabhängig. Aus diesem Grund wird sie auch als Ortsfaktor bezeichnet. Der Ortsfaktor besitzt ebenfalls das Formelzeichen
am größten. Die Fallbeschleunigung ist also ortsabhängig. Aus diesem Grund wird sie auch als Ortsfaktor bezeichnet. Der Ortsfaktor besitzt ebenfalls das Formelzeichen ![]() . Die Einheit des Ortsfaktors ist jedoch oft Newton pro Kilogramm
. Die Einheit des Ortsfaktors ist jedoch oft Newton pro Kilogramm ![]() , da er aussagt, wie groß die Gewichtskraft eines Körpers pro Kilogramm Masse an einem Ort ist.
, da er aussagt, wie groß die Gewichtskraft eines Körpers pro Kilogramm Masse an einem Ort ist.
Es gilt also:
![]()
Die Einheit ![]() kürzt sich heraus und übrig bleibt die Einheit der Fallbeschleunigung Meter pro Sekunde ins Quadrat
kürzt sich heraus und übrig bleibt die Einheit der Fallbeschleunigung Meter pro Sekunde ins Quadrat ![]() .
.
Für die Erdoberfläche sagt der Ortsfaktor ![]() aus, dass ein Körper, der eine Masse von
aus, dass ein Körper, der eine Masse von ![]() hat, eine Gewichtskraft von
hat, eine Gewichtskraft von ![]() besitzt.
besitzt.
Der Ortsfaktor und die Fallbeschleunigung beschreiben also den gleichen Wert. Auch wird manchmal der Begriff Erdbeschleunigung ![]() verwendet. Auch die Erdbeschleunigung wird in der Einheit
verwendet. Auch die Erdbeschleunigung wird in der Einheit ![]() angegeben.
angegeben.
Berechnung der Fallbeschleunigung
Es gibt verschiedene Methoden, die Fallbeschleunigung an einem Ort zu bestimmen. Drei verschiedene Varianten wollen wir genauer betrachten.
Newtonsches Gesetz
Die Formel für die Gewichtskraft lautet nach dem zweiten newtonschen Gesetz:
![]()
Diese Gleichung nach ![]() umgestellt ergibt:
umgestellt ergibt:
![]()
Dabei ist:
 : Gewichtskraft in
: Gewichtskraft in 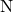
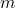 : Masse in
: Masse in 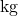
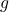 : Fallbeschleunigung in
: Fallbeschleunigung in 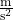 .
.
Sind Masse und Gewichtskraft eines Körpers bekannt, kann die Erdbeschleunigung mit dieser Formel berechnet werden.
Weg-Zeit-Gesetz des freien Falls
Stellt man das Weg-Zeit-Gesetz des freien Falls nach der Beschleunigung um, erhält man die Formel zur Berechnung der Fallbeschleunigung:
Weg-Zeit-Gesetz: ![]()
Fallbeschleunigung: ![]()
Dabei ist:
 : Fallweg
: Fallweg 
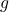 : Fallbeschleunigung
: Fallbeschleunigung 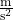
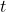 : Fallzeit in
: Fallzeit in 
Sind Fallweg und Fallzeit bekannt, kann die Fallbeschleunigung mit dieser Formel berechnet werden. Aber auch die Fallzeit kann berechnet werden, wenn die Fallbeschleunigung und der Fallweg bekannt sind.
Fallbeschleunigung mithilfe des Fadenpendels berechnen
Eine dritte Möglichkeit ist es, die Gesetze für das Fadenpendel zu nutzen. Für die Schwingungsdauer ![]() eines Fadenpendels gilt:
eines Fadenpendels gilt:
![]()
Auch diese Formel kann nach ![]() umgestellt werden und wir erhalten:
umgestellt werden und wir erhalten:
![]()
Dabei ist:
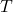 : Schwingungsdauer in
: Schwingungsdauer in 
 : Länge des Pendels in
: Länge des Pendels in 
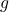 : Fallbeschleunigung in
: Fallbeschleunigung in 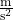
Die Schwingungsdauer ![]() und die Länge des Pendels
und die Länge des Pendels ![]() können in einem Versuchsaufbau gemessen werden. Sind beide Werte bekannt, kann
können in einem Versuchsaufbau gemessen werden. Sind beide Werte bekannt, kann ![]() berechnet werden.
berechnet werden.
Fallbeschleunigung auf anderen Himmelskörpern
Auch auf anderen Himmelskörpern gibt es Fallbeschleunigung und Ortsfaktor. Um die Fallbeschleunigung dort zu berechnen, nutzen wir das zweite newtonsche Gesetz und das Gravitationsgesetz.
zweites newtonsches Gesetz: ![]()
Gravitationsgesetz: ![]()
Dabei ist:
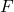 : Kraft in
: Kraft in 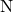
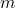 : Masse Körper in
: Masse Körper in 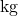
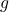 : Fallbeschleunigung in
: Fallbeschleunigung in 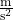
 : Gewichtskraft in
: Gewichtskraft in 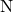
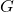 : Gravitationskonstante
: Gravitationskonstante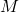 : Masse des Himmelskörpers in
: Masse des Himmelskörpers in 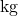
 : Radius des Himmelskörpers in
: Radius des Himmelskörpers in 
Die Gravitationskonstante ist eine Naturkonstante und definiert als:
![]()
Dabei entspricht die Kraft des newtonschen Gesetzes der Gewichtskraft, es gilt: ![]() . Beide Formeln können also gleichgesetzt und nach
. Beide Formeln können also gleichgesetzt und nach ![]() umgestellt werden.
umgestellt werden.
![]()
![]()
Mit dieser Formel lässt sich die Fallbeschleunigung auf der Oberfläche jedes Himmelskörpers berechnen.
Ortsfaktoren verschiedener Himmelskörper
Die folgende Tabelle zeigt die Ortsfaktoren verschiedener Himmelskörper. Da dieser abhängig von Masse und Radius des Himmelskörpers ist, sind diese beiden Größen ebenfalls angegeben.
| Himmelskörper | Ortsfaktor in |
Masse in |
Radius in |
|---|---|---|---|
| Erde | 9,81 | 5,97 |
|
| Mond | 1,62 | 7,34 |
|
| Sonne | 275 | 2,00 |
|
| Mars | 3,72 | 6,41 |
Häufig gestellte Fragen zum Thema Ortsfaktor und Fallbeschleunigung