Transformator – Aufbau, Funktion und Formeln

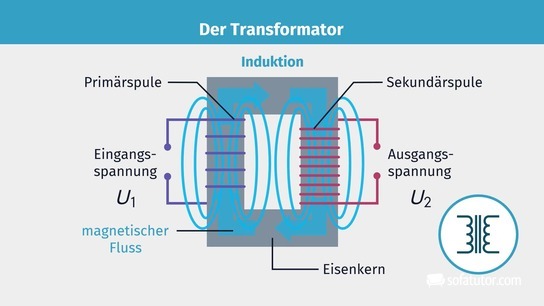
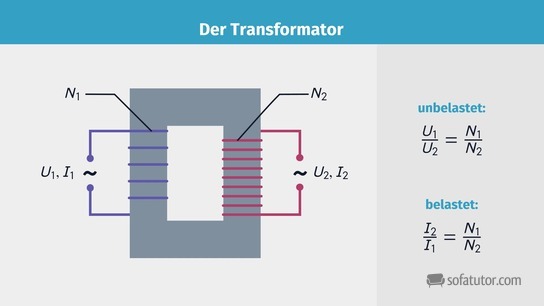
Um sich die Wirkungsweise eines Transformators besser veranschaulichen zu können, ist es hilfreich, sich zunächst den Aufbau genauer anzuschauen. In der beschrifteten Skizze ist im Folgenden der Transformator zusammen mit dem in der Physik für Schaltpläne gebräuchlichen Schaltzeichen gezeigt.

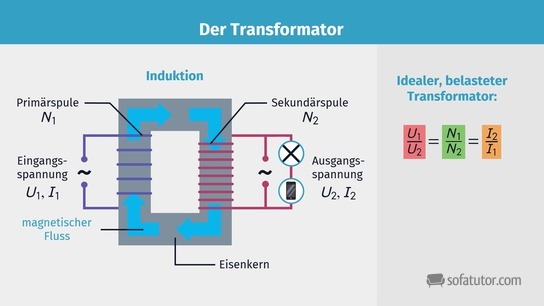
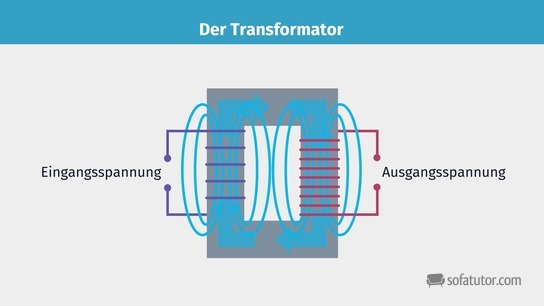
Der Grundaufbau des Transformators (kurz: Trafo) ist im Grunde recht einfach erklärt. Er besteht aus zwei Spulen und einem Eisenkern. Damit der Trafo auch etwas transformiert, ist es hierbei wichtig, dass die beiden Spulen unterschiedliche Windungszahlen N haben. Wird nun an die Primärspule eine Wechselspannung angelegt, führt diese in der Primärspule zu einer Änderung des magnetischen Flusses. Diese Änderung wird nun mithilfe des Eisenkerns auf die Sekundärspule übertragen. Dies führt dazu, dass in der Sekundärspule ein Wechselstrom induziert wird. Die Spannung des induzierten Wechselstroms hängt hierbei mit der an der Primärspule anliegenden Spannung sowie dem Verhältnis der Windungszahlen von Primär- und Sekundärspule zusammen.

Wie wir bereits gesehen haben, führt eine an der Primärspule angelegte Spannung aufgrund des Induktionsgesetzes zu einer Änderung des magnetischen Flusses.

Das Induktionsgesetz gilt aber auch für die Sekundärspule und führt in dieser aufgrund der Änderung des magnetischen Flusses zur Induktion einer Spannung.

Da die Änderung des Flusses in beiden Fällen gleich ist, können beide Gleichungen gleichgesetzt werden. Man erhält auf diesem Weg folgende Formel.

Damit lässt sich zum Beispiel für eine an der Primärspule angelegte Spannung die in der Sekundärspule induzierte Spannung berechnen.
Diese Formel gilt allerdings nur, solange kein Strom innerhalb der Spule fließt. Dies ist jedoch nur für unbelastete Transformatoren der Fall, da der Stromkreis in diesen nicht geschlossen ist. Schließt man nun den Stromkreis der Sekundärspule mithilfe eines Verbrauchers oder eines Widerstands, fließt ein Strom innerhalb der Sekundärspule. Dieser Fall wird als belasteter Transformator bezeichnet. Für diesen Fall ist es deshalb häufig interessant, die induzierte Stromstärke zu kennen. Da wir hier annehmen, dass es sich um einen idealen Transformator handelt, also der Transformator einen Wirkungsgrad von hat, gilt, dass die dem Transformator auf der Primärspule zugeführte Leistung der von der Sekundärspule abgegebenen Leistung entsprechen muss. Diese Annahme führt dazu, dass sich die Stromstärken im Vergleich zu den Spannungen umgekehrt proportional zu den Windungszahlen verhalten, da gilt . Es gilt demnach:

Rein praktisch gilt diese Formel nur näherungsweise bei sehr kleinen Widerständen im Sekundärstromkreis und sehr verlustarmer Bauweise.

Transformatoren finden heutzutage in jedem Ladekabel Verwendung, um den Strom aus der Steckdose korrekt für den Verbraucher anzupassen. Aber auch auf dem Weg vom Kraftwerk zur Steckdose werden Transformatoren eingesetzt. So wird der vom Kraftwerk erzeugte Strom zu einer Hochspannung transformiert, da so die Verluste in den Überlandleitungen reduziert werden können. Damit der Strom jedoch in Wohnungen wieder genutzt werden kann, muss dieser anschließend zwischen der Überlandleitung und der Wohnung in einem Umspannwerk zurücktransformiert werden. Du siehst also, dass auch ein so einfaches Bauteil einen sehr großen Einfluss auf unser aller Leben haben kann.