Das plancksche Wirkungsquantum – Definition und Begriffe
Lerne alles über das einzigartige plancksche Wirkungsquantum, eine fundamentale Naturkonstante, die die Energie eines Photons mit der Lichtfrequenz verbindet. Von Max Planck entdeckt, hat es die Physik revolutioniert. Möchtest du mehr über die Ultraviolettkatastrophe, den Fotoeffekt und die Lichtquantenhypothese erfahren?
Inhaltsverzeichnis zum Thema Plancksches Wirkungsquantum
Das plancksche Wirkungsquantum – Entdeckung und Erklärung
Ende des 19. Jahrhunderts schien es, als wäre die Physik abgeschlossen. Nur zwei Probleme waren ungelöst: die sogenannte Ultraviolettkatastrophe und der Fotoeffekt.
Die Ultraviolettkatastrophe
Die Ultraviolettkatastrophe stand im Zusammenhang mit der Untersuchung der Spektren glühender Körper, zum Beispiel Glühdrähten. Diese hängen vor allem von der Temperatur des Körpers ab, weshalb das Modell dafür der sogenannte schwarze Körper oder auch Hohlraumstrahler ist.
Ein solcher Körper ist ein Kasten mit schwarzen Wänden und einem winzig kleinen Loch, der von einer Heizspirale auf konstanter Temperatur gehalten wird. Auf diese Weise verschluckt der Körper alle einfallende Strahlung und emittiert (d. h. =sendet aus) eine Strahlung, die ausschließlich von seiner Temperatur abhängt.
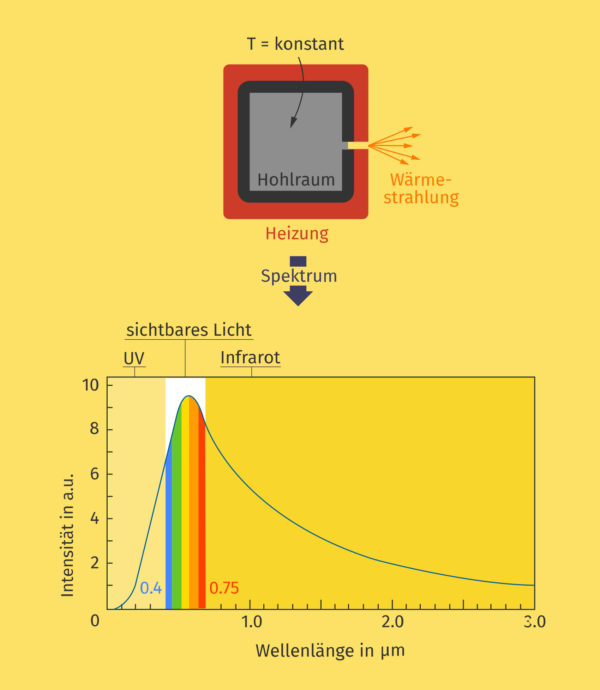
Die Abbildung zeigt das reale Spektrum eines solchen Hohlraumstrahlers; die Intensität ist dabei in sogenannten arbitrary units, (a.u.) angegeben, also beliebigen Einheiten, da es nur auf den Verlauf der Kurve ankommt, nicht auf die konkreten Zahlenwerte.
Das Problem war nur, dass man diese Kurve nicht theoretisch erklären konnte. Es gab mathematische Modellierungen für kleine Wellenlängen und solche für größere Wellenlängen. Nur passten diese nicht zusammen. Und das Modell für größere Wellenlängen, das Rayleigh-Jeans-Gesetz, sagte für kleine Wellenlängen, also den ultravioletten Spektralbereich, eine unendlich hohe Intensität voraus – was natürlich nicht sein kann. Katastrophe!
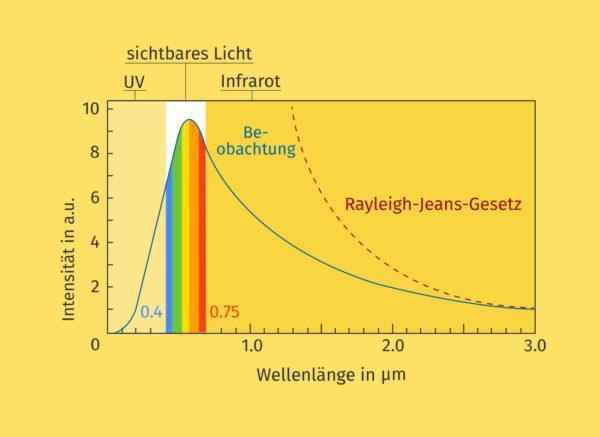
Das plancksche Strahlungsgesetz
Max Planck entwickelte zunächst eine Formel, die den experimentellen Verlauf der Strahlungskurve exakt nachbildete, und lieferte zwei Monate danach eine theoretische Erklärung seines Strahlungsgesetzes.
Seine Idee besteht darin, dass die Atome des schwarzen Körpers Energie nicht in beliebigen Beträgen aufnehmen oder abgeben können, sondern nur in Portionen.
Die Konstante, die er dafür einführen musste, nannte er zunächst Hilfskonstante, daher der Buchstabe ![]() . Der 14.12.1900, der Tag, an dem er diese Idee in einem Vortrag in Berlin vorstellte, gilt als der Geburtstag der Quantenphysik.
. Der 14.12.1900, der Tag, an dem er diese Idee in einem Vortrag in Berlin vorstellte, gilt als der Geburtstag der Quantenphysik.
Ihm und seinen Zuhörern war allerdings nicht klar, dass die Portioniertheit der Energie nicht nur für den schwarzen Körper zutraf, sondern dass sich dahinter eine physikalische Grundtatsache verbarg – die auch das andere noch offene Problem der Physik lösen konnte.
Der Fotoeffekt
Bei der Bestrahlung von Metalloberflächen mit Licht werden geladene Teilchen herausgelöst.
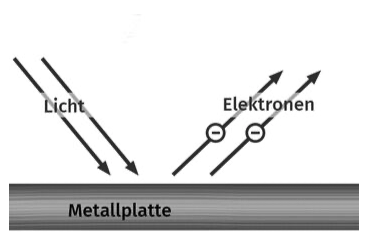
Seit 1899 wusste man, dass es sich hierbei um Elektronen handelte und dass die Energie dieser Elektronen nicht etwa von der Intensität, sondern von der Frequenz bzw. Wellenlänge des Lichts abhängt. Die Intensität beeinflusst nur die Anzahl der Elektronen, nicht aber deren einzelne Energien. Außerdem gab es eine materialabhängige Grenzfrequenz ![]() , unterhalb derer kein Effekt eintrat. Wenn der Effekt eintrat, dann sofort.
, unterhalb derer kein Effekt eintrat. Wenn der Effekt eintrat, dann sofort.
Dies ist mit der Wellentheorie des Lichts nicht zu erklären. Die Energie einer Welle steckt eben vor allem in ihrer Intensität, wie man sich leicht an einer Wasserwelle oder Schallwelle klar machen kann. Und man würde erwarten, dass auch kleinere Energien sich im Material ansammeln und aufaddieren würden.
Die Lichtquantenhypothese
Albert Einstein hatte nun im Jahr 1905 die Idee, dass Plancks Idee der Energieportionen auch auf den Fotoeffekt übertragen werden könnte. Dazu musste er die Wellentheorie des Lichts erst einmal vergessen.
„Nach der hier ins Auge zu fassenden Annahme ist bei Ausbreitung eines von einem Punkte ausgehenden Lichtstrahls die Energie nicht kontinuierlich auf größer und größer werdende Räume verteilt, sondern es besteht dieselbe aus einer endlichen Zahl von in Raumpunkten lokalisierten Energiequanten, welche sich bewegen, ohne sich zu teilen und nur als Ganze absorbiert oder erzeugt werden können.“
Einstein, Albert. ‚Ueber einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt‘. Annalen der Physik, 17 (1905), S. 133.
Wenn das Licht aus einem Strom von Energieportionen, die Einstein Energiequanten oder Lichtquanten nannte, bestehen würde, von denen jede ein einzelnes Elektron herauslöst, dann würde eine hohe Lichtintensität einfach eine hohe Zahl an Energieportionen bedeuten. Und die Energie einer solchen Energieportion wäre dann eben, warum auch immer, von der Wellenlänge des Lichts bzw. seiner Frequenz abhängig. Die Grenzfrequenz wäre dann auch erklärbar: Es ist eine bestimmte Auslösearbeit nötig, damit das Elektron das Metall verlässt. Und nur wenn die Energieportion mehr Energie an das Elektron abgibt, kann das Elektron das Metall verlassen.
Auch Einstein konnte nicht erklären, wie dieses Modell von Energieportionen, die man später Photonen nannte, mit dem Wellenmodell des Lichts, dass experimentell und theoretisch sehr gut bestätigt war, zusammengebracht werden konnte. Seine Annahme, dass die Energie eines Lichtquants über das plancksche Wirkungsquantum ![]() mit der Frequenz
mit der Frequenz ![]() des Lichts zusammenhängt, konnte auf der anderen Seite ebenfalls sehr gut experimentell bestätigt werden:
des Lichts zusammenhängt, konnte auf der anderen Seite ebenfalls sehr gut experimentell bestätigt werden:
![]()
Die Gegenfeldmethode
Die folgende Abbildung zeigt einen experimentellen Aufbau zur Messung des sogenannten Fotostroms. Die aus der Kathode austretenden Elektronen werden durch eine Saugspannung zur Anode hin beschleunigt.
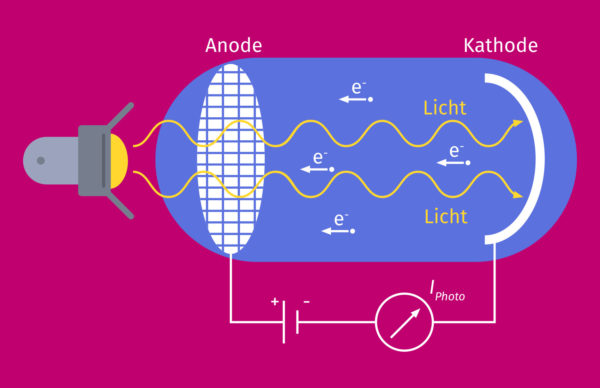
Eine Steigerung der Intensität des Lichts führt zu einer Erhöhung des Fotostroms. Dies könnte bedeuten, dass die Elektronen schneller geworden sind oder dass mehr Elektronen ausgelöst wurden.
Wenn man die Spannung umdreht, werden die Elektronen abgebremst. Dies nennt man die Gegenfeldmethode. Man kann nun für verschiedene Frequenzen jeweils die Spannung einstellen, bei der der Fotostrom zusammenbricht, also null wird. Diese Spannung ergibt mit der Elementarladung multipliziert die kinetische Energie der Elektronen. Da der Fotostrom bei einem Material bei einer bestimmten Frequenz immer bei der gleichen Gegenspannung null wird, haben wohl alle Elektronen bei der gleichen Frequenz die gleiche maximale kinetische Energie. Dann bedeutet ein höherer Fotostrom bei höherer Lichtintensität offenbar nur mehr Elektronen, nicht schnellere.
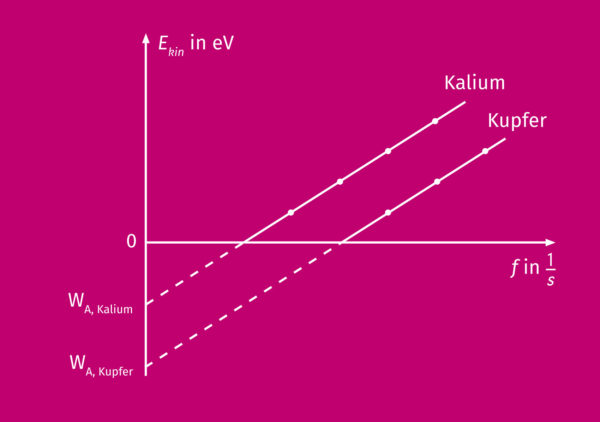
Man stellt fest, dass für jedes Material eine spezielle Gerade, die Einsteingerade, aufgenommen werden kann. Alle Geraden haben aber die gleiche Steigung – das plancksche Wirkungsquantum.
Aus dem gezeigten Graphen ließ sich Einsteins Idee unmittelbar ablesen. Die Geradengleichung ist:
![]()
Die Energie eines Lichtquants teilt sich demzufolge auf in die Auslösearbeit und die kinetische Energie des Elektrons:
![]()
Das Photon
Die Energie eines einzelnen Photons beträgt ![]() . In alten Texten findet sich manchmal auch der Ausdruck
. In alten Texten findet sich manchmal auch der Ausdruck ![]() , da der griechische Buchstabe
, da der griechische Buchstabe ![]() früher auch für die Frequenz verwendet wurde.
früher auch für die Frequenz verwendet wurde.
Im gleichen Jahr, in dem Einstein das Lichtquant erdachte, bewies er auch die Äquivalenz von Masse und Energie in der berühmten Formel ![]() .
.
Damit ergibt sich als Masse des Photons der Ausdruck:
![]()
Aufgrund des Zusammenhangs zwischen der Wellenlänge ![]() , der Frequenz
, der Frequenz ![]() und der Lichtgeschwindigkeit
und der Lichtgeschwindigkeit ![]()
![]()
ergibt sich der folgende Ausdruck für die Masse des Photons:
![]()
Der Impuls ![]() eines Körpers ist das Produkt aus seiner Masse
eines Körpers ist das Produkt aus seiner Masse ![]() und seiner Geschwindigkeit
und seiner Geschwindigkeit ![]() . – Geht man nun davon aus, dass sich das Photon mit der Lichtgeschwindigkeit
. – Geht man nun davon aus, dass sich das Photon mit der Lichtgeschwindigkeit ![]() bewegt, ergibt sich für seinen Impuls
bewegt, ergibt sich für seinen Impuls ![]() :
:
![]()
Dabei ergeben sich aber gleich mehrere Probleme. Das Photon wird mit der Zuordnung einer Masse und eines Impulses eindeutig zu einem echten Teilchen.
Wie aber kann ein Teilchen eine Wellenlänge oder eine Frequenz haben, also eindeutige Welleneigenschaften? Dieser Widerspruch ist der sogenannte Welle-Teilchen-Dualismus. Licht verhält sich in manchen Situationen wellenartig, wie etwa bei Interferenzerscheinungen, in anderen Situation teilchenartig, wie beim Fotoeffekt oder dem Comptoneffekt. Es ist sinnlos, von der Frequenz eines Photons zu sprechen. Sinnvollerweise spricht man von der Frequenz des Lichts und meint damit die Frequenz der Welle.
Ein zweites Problem ergibt sich aus der speziellen Relativitätstheorie Einsteins. Wie kann sich denn ein Teilchen mit Lichtgeschwindigkeit bewegen? Die Masse eines Teilchen wird doch immer größer, je mehr sich seine Geschwindigkeit der Lichtgeschwindigkeit annähert.
Diese Aussage gilt für Teilchen, die eine Ruhemasse haben. Das Photon ist ein Ausnahmeteilchen. Seine Ruhemasse ist null oder anders ausgedrückt: Es hat einfach immer Lichtgeschwindigkeit.
Das plancksche Wirkungsquantum – Zahlenwert und Einheiten
Das plancksche Wirkungsquantum in ![]()
Das plancksche Wirkungsquantum hat seinen Namen von der physikalischen Größe Wirkung, die definiert ist als Produkt aus Energie und Zeit.
Sein Wert beträgt ![]() .
.
Da das plancksche Wirkungsquantum seit 2019 als Grundlage für die Definition der Basiseinheiten im internationalen Einheitensystem dient, ist der obige Wert festgelegt und damit ein exakter Wert.
In der Schule ist es üblich, mit gerundeten Werten zu arbeiten, wie etwa ![]() oder auch
oder auch ![]() .
.
Das plancksche Wirkungsquantum in ![]()
Es ist häufig nützlich, das plancksche Wirkungsquantum in der Einheit ![]() zu verwenden.
zu verwenden.
Dann gilt:
![]()
Hier sind gute Rundungswerte für die Schule ![]() oder auch
oder auch ![]() .
.
Das reduzierte plancksche Wirkungsquantum
In manchen Gleichungen tritt auch das sogenannte reduzierte plancksche Wirkungsquantum ![]() auf, das gelegentlich als diracsche Konstante bezeichnet wird, manchmal sogar auch als heisenbergsche Konstante, was aber in der Physik nicht üblich ist.
auf, das gelegentlich als diracsche Konstante bezeichnet wird, manchmal sogar auch als heisenbergsche Konstante, was aber in der Physik nicht üblich ist.
Häufig gestellte Fragen zum Thema Plancksches Wirkungsquantum

