Mechanische Schwingungen – Definitionen, Begriffe und Beispiele

Erfahre, dass mechanische Schwingungen periodische Bewegungen um die Gleichgewichtslage sind. Grundbegriffe wie Elongation, Amplitude und Frequenz spielen dabei eine wichtige Rolle. Möchtest du wissen, wie harmonische Schwingungen funktionieren und welche Rolle lineare Kraftgesetze dabei spielen? Dies und vieles mehr findest du im folgenden Text!

Inhaltsverzeichnis zum Thema Mechanische Schwingungen

Mechanische Schwingungen im Überblick

  • Eine mechanische Schwingung ist eine periodische Bewegung um die Gleichgewichtslage.

  • Wichtige Grundbegriffe sind die Elongation y(t), Amplitude \hat{y}, Periodendauer T und Frequenz f.

  • Harmonische Schwingungen lassen sich mit Sinus- oder Cosinusfunktion beschreiben. Es gilt für sie das lineare Kraftgesetz F = - D\cdot y.

Mechanische Schwingungen – Lernvideo

Quelle sofatutor.com

Mechanische Schwingungen einfach erklärt

Eine mechanische Schwingung ist eine periodische Bewegung um die Gleichgewichtslage herum (die auch Nulllage oder Ruhelage genannt wird). Periodisch bedeutet dabei, dass sich ein Bewegungszustand nach festen Zeitabschnitten wiederholt. 

Dabei ist die Gleichgewichtslage der Punkt, an dem der schwingende Körper in Ruhe ist, bevor er durch eine externe Kraft ausgelenkt und damit dem System Energie zugeführt wird. 

Mechanische Schwingung – Definitionen der Grundbegriffe

Um Schwingungen zu beschreiben, benötigen wir folgende Grundbegriffe:

Die Elongation y(t) ist die momentane Auslenkung des schwingenden Körpers aus seiner Ruhelage.
Die maximale Elongation wird Amplitude \hat{y} genannt. Dieses Maximum der Auslenkung ist in den Umkehrpunkten der Bewegung erreicht.
Die Periodendauer mit dem Formelzeichen T, auch Periodenlänge oder Schwingungsdauer genannt, ist die Zeit, die für einen kompletten Schwingungszyklus benötigt wird.
Die Frequenz f beschreibt die Anzahl an Schwingungen pro Sekunde. Sie ist der Kehrwert der Periodendauer:
f=\frac{1}{T}

Die Einheiten der vorangegangenen physikalischen Größen sind:
[y(t)] = 1\,m ; [\hat{y}] = 1\,m ; [T] = 1\,s ; [f] = 1\,Hz

Harmonische Schwingung – Definition

Eine Schwingung wird dann als harmonisch bezeichnet, wenn eine der folgenden Voraussetzungen erfüllt ist. Dabei ist zu beachten, dass diese sich gegenseitig bedingen, also ist die eine erfüllt, ist die andere ebenfalls erfüllt. 

Harmonische Schwingung – Projektion einer gleichförmigen Kreisbewegung

Projiziert man die gleichförmige Kreisbewegung eines Körpers auf einen Schirm, indem man die Kreisbewegung von der Seite her beleuchtet, sieht man als Schatten auf dem Schirm eine geradlinige Schwingungsbewegung.
Diese Schwingungsbewegung kann durch eine Sinusfunktion bzw. Cosinusfunktion beschrieben werden.
Eine nicht harmonische Schwingung lässt sich also nicht als Sinusfunktion beschreiben.

Harmonische Schwingung – lineares Kraftgesetz

Zieht man am Körper eines Federschwingers, gibt es aufgrund der Spannung der Feder eine Kraft, die dieser Auslenkung entgegenwirkt, da das System wieder in die Ruhelage gelangen möchte. Diese Rückstellkraft F ist also der Richtung der Elongation entgegengesetzt und damit in jedem Moment zur Gleichgewichtslage hin gerichtet (gekennzeichnet durch das Minus auf der rechten Seite in der folgenden Formel). Betraglich ist F proportional zur Elongation

F= -D \cdot y(t)

wobei D die Richtgröße ist, die im Fall des Federpendels Federkonstante genannt wird, mit der Einheit [D] = 1\, \frac{\text{N}}{\text{m}}}.

Ein Federpendel z. B. ist ein sogenannter harmonischer Oszillator.

Harmonische Schwingung – Bewegungsgleichung

Harmonische Schwingungen lassen sich also als Sinus- bzw. Cosinusfunktion beschreiben. 

Harmonische Schwingung

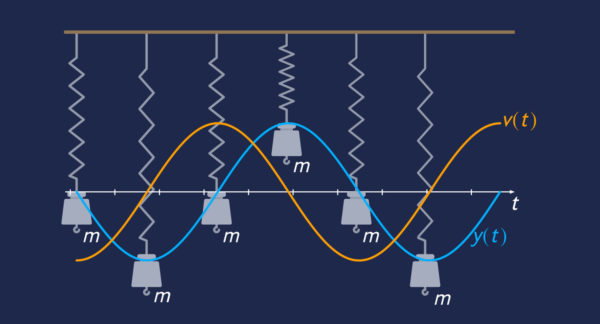
Wir entscheiden uns für die Sinusfunktion:

y(t) = \hat{y} \cdot \sin(\omega \cdot t + \varphi_0)
\hat{y} steht für die Amplitude und \omega = 2\pi f beschreibt die Kreisfrequenz bzw. Winkelgeschwindigkeit der Schwingung.
\varphi_0 ist der Phasenwinkel zum Zeitpunkt t= 0s.
Der Phasenwinkel kennzeichnet den momentanen Schwingungszustand eines harmonischen Oszillators. Er ist das Argument der Sinusfunktion. Es gilt also:
\varphi = \omega \cdot t + \varphi_0
Markante Schwingungszustände und damit Phasenwinkel sind die Gleichgewichtslage (\varphi = 0, \pi) und Umkehrpunkte (\varphi = \frac{\pi}{2} oder \varphi= \frac{3 \pi}{2}).

Durch einmaliges Ableiten der Bewegungsgleichung y(t) bestimmt man die Geschwindigkeit v(t), durch zweimaliges wiederum die Beschleunigung a(t).
Somit erhalten wir:
\\ (1)~y(t) = \hat{y} \cdot \sin(\omega \cdot t + \varphi_0) \\ (2)~v(t) = \hat{v} \cdot \cos(\omega \cdot t + \varphi_0)\\ (3)~a(t) = - \hat{a} \cdot \sin(\omega \cdot t + \varphi_0)

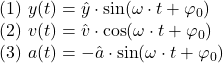
\hat{v} bzw. \hat{a} beschreiben die Amplitude von v und a.

Folgende Tabelle gibt an, für welche Phasenwinkel s, v, und a null bzw. maximal sind:

s v a
\varphi= 0 (Ruhelage) null maximal null
\varphi_0 = \frac{\pi}{2} (Umkehrpunkt) maximal null maximal
\varphi_0 = \pi (Ruhelage) null maximal null
\varphi_0= \frac{3\pi}{2} (Umkehrpunkte maximal null maximal

In der Gleichgewichtslage ist also die Elongation und Beschleunigung null, da keine Rückstellkraft wirkt, jedoch ist die Geschwindigkeit maximal.
In den Umkehrpunkten hingegen ist die Auslenkung maximal und der Körper wird maximal zur Ruhelage zurück beschleunigt. Die Geschwindigkeit ist hier null, da sich das Vorzeichen, also die Richtung der Bewegung ändert.

Harmonische Schwingung – Energie

Da wir bisher keine Dämpfung, z. B. durch Reibung, berücksichtigen, sprechen wir über ungedämpfte Schwingungen. Bei diesen setzt sich die Gesamtenergie des Systems zu einem beliebigen Zeitpunkt aus der potenziellen und kinetischen Energie zusammen:
E_\text{ges} = E_\text{pot} + E_\text{kin}

Die potenzielle Energie wird beim Federpendel durch folgende Formel beschrieben:
E_\text{pot} = \frac{1}{2} D (y(t))^2

Die kinetische Energie wird mit
E_\text{kin} = \frac{1}{2} m(v(t))^2
angegeben.

Da in den Umkehrpunkten die Geschwindigkeit null ist, ist hier die maximale potenzielle Energie zu finden. In der Gleichgewichtslage ist die potenzielle Energie null und damit die kinetische Energie maximal.
Die Gesamtenergie kann man berechnen, indem man die maximale potenzielle oder maximale kinetische Energie berechnet:

E_\text{ges} = \frac{1}{2} D \hat{y}^2 = \frac{1}{2} m \hat{v}^2

Gedämpfte Schwingung

Bisher haben wir nur über ungedämpfte Schwingungen gesprochen. Jedoch gibt es in jedem System Dämpfung durch z. B. Reibung. Dabei gibt das schwingende System Energie nach außen ab, die Amplitude wird bei jeder Schwingung kleiner.
Manchmal wird in ein System aber auch eine Dämpfung eingebaut, damit es nicht zur sogenannten Resonanz kommt, die ein System schädigen kann.
So werden z. B. in Autos Stoßdämpfer eingebaut.

Schwingungen – Beispiele

Wie schon erwähnt ist das Federpendel ein harmonischer Oszillator, der harmonische Schwingungen bildet. Ebenso kann ein Fadenpendel  für kleine Winkel als harmonischer Oszillator dienen: 

Fadenpendel

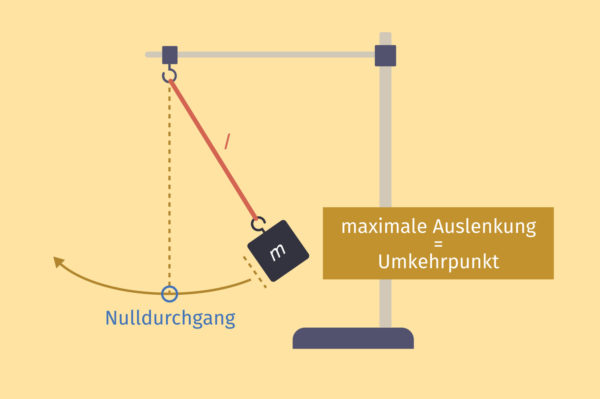
Hier hängt eine Masse an einem Faden und wird aus ihrer Ruhelage (nach unten hängend) ausgelenkt und pendelt hin und her. 

Weitere Beispiele für mechanische Schwingungen sind die Schwingung einer Saite eines Musikinstruments. Diese ist jedoch nicht harmonisch, aber als Überlagerung von harmonischen Schwingungen darstellbar. 

Häufig gestellte Fragen zum Thema Mechanische Schwingungen

Eine mechanische Schwingung ist eine Hin- und Herbewegung, die sogenannte Gleichgewichtslage. Sie ist somit eine periodische Bewegung.

Eine mechanische Schwingung entsteht durch Auslenkung aus der Gleichgewichtslage aufgrund einer externen Kraft. Nehmen wir zum Beispiel ein Federpendel: Eine Feder ist oben befestigt, unten hängt eine Masse dran. Nun ziehst du an dieser Masse und lenkst somit die Feder aus. Lässt du los, so zieht sich die Feder zusammen, aufgrund der Trägheit der Masse schießt sie aber über die Gleichgewichtslage hinaus, bis sich im oberen Umkehrpunkt die Richtung der Bewegung umdreht und der Körper sich aufgrund der Gewichtskraft nach unten bewegt. 

Zum Beispiel, wenn ein Auto über eine Bodenwelle fährt oder bei Saiten eines Musikinstruments. 

Es muss schwingungsfähig und aus seiner Ruhelage auslenkbar sein. Das System muss so aufgebaut sein, dass es eine Rückstellkraft gibt. 

Harmonische Schwingungen können als Sinus- oder Cosinuskurve dargestellt werden. 

Sie kann nicht durch eine Sinus- oder Cosinusfunktion beschrieben werden, wie z. B. die Schwingung von Stimmbändern. 

Leave A Comment

Alle Artikel aus dem Fach Physik